Lektion STE04: Quadratische Pyramide
Um die Lektion verstehen zu können, müsst ihr unbedingt den Satz des Pythagoras beherrschen. Wer ihn noch nicht anwenden kann, schaut sich die Lektion vorher an, ansonsten könnt ihr die Herleitungen der Formeln nicht verstehen.
Zu den Pyramiden gibt es vieles neues interessantes Wissen, viel Spaß dabei:
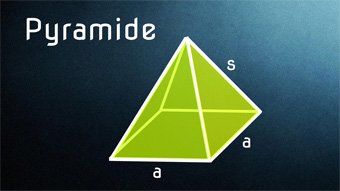
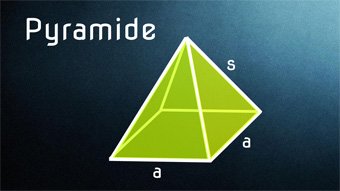
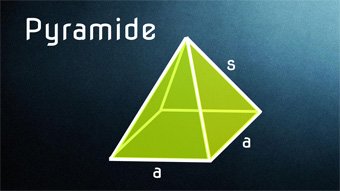
Quadratische Pyramide - Bestandteile, Herleitung Formeln
Bestandteile der Pyramide: Seite a, Höhe der Pyramide h, Seitenkante s, Höhe auf Seite a, Diagonale d, Grundfläche, Seitenfläche, Oberfläche, Volumen. Herleitung der Formeln für die Seitenkante s und die Höhe h_a sowie für die Diagonale. Unterschied gerade und schiefe Pyramide.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
STE04-2 Quadratische Pyramide - Herleitung Flächenformeln, VolumenWir leiten die Formeln für Umfang, Grundfläche, Mantelfläche, Oberfläche her. Wir zeigen, wie die Volumenformel lautet und wie man sie sich besser merken kann. Am Ende fassen wir alle Formeln zu den Pyramiden zusammen.
-
STE04-3 Quadratische Pyramide - AufgabenZuerst Übersicht aller Formeln. Dann lösen wir die Aufgabe: Gegeben sind Höhe h und Seite a und wir berechnen alle Bestandteile der Pyramide. Nächste Aufgabe: Es sind nur Seite a und Oberfläche gegeben, die Höhe ist zu bestimmen.
-
STE04-4 Quadratische Pyramide - Aufgaben IIWir stellen eine Formel für Seite a auf, wenn nur Seitenkante s und Mantelfläche M gegeben sind. Wir substituieren und prüfen auf Scheinlösungen, um das korrekte Ergebnis zu ermitteln.
Hier findet ihr den Pyramiden-Rechner, den wir im Video einsetzen:
Hier findest du 3 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Höhen- und Oberflächenberechnung einer quadratischen Pyramide
- Höhe, Volumen und Oberflächeninhalt einer geraden Pyramide berechnen
- Grundfläche einer Pyramide berechnen - V und h gegeben
- Wie ist die Formel zur Berechnung der Höhe einer quadratischen Pyramide?
- Satz des Pythagoras in einer Pyramide anwenden
- Thema Geometrie: Berechne hs, h und V einer quadratischen Pyramide mit Oberfläche 39,2 cm²
- Wie viele Dachziegel passen auf den Flächeninhalt 25,0695?
Finde weitere Fragen und Antworten in der Mathelounge.