Lektion G07: Binomische Formeln
Heute schauen wir uns an, wie die Binomischen Formeln entstehen. Dazu verwenden wir insbesondere das Distributivgesetz.
In diesen Videos werden alle drei binomischen Formeln ausführlich und verständlich hergeleitet, damit ihr besser Mathe lernen und eine bessere Note schreiben könnt. Los geht es:
Binomische Formeln - Voraussetzungen
(Erweitertes) Distributivgesetz, Berechnung der Fläche von Rechteck und Quadrat, Zahl ins Quadrat (a·a = a²), 2·ab = ab + ab, Zerlegen einer Strecke in Teilstrecken.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G07-2 Binomische Formeln - Erste Binomische FormelHerleitung der 1. Binomischen Formel, Grafischer Nachweis der 1. Binomischen Formel über Flächen.
-
G07-3 Binomische Formeln - Zweite Binomische FormelHerleitung der 2. Binomischen Formel, Grafischer Nachweis, Anwendung bei der Aufgabe (3xy-5)²
-
G07-4 Binomische Formeln - Dritte Binomische FormelHerleitung der 3. Binomischen Formel, Faktorisieren, Schnelleres Kopfrechnen mit Binomischen Formeln.
-
 Binomische Formel (1)Die 1. Binomische Formel wird hier grafisch veranschaulicht. Die Fläche (a+b)² entspricht der Fläche a²+2·ab+b².
Binomische Formel (1)Die 1. Binomische Formel wird hier grafisch veranschaulicht. Die Fläche (a+b)² entspricht der Fläche a²+2·ab+b². -
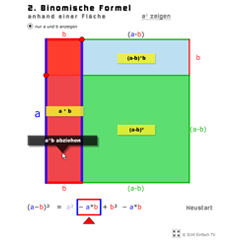 Binomische Formel (2)Die 2. Binomische Formel grafisch in Form von Flächen dargestellt. (a-b)² = a² - 2·a·b + b². Bitte lest euch die Einleitung durch.
Binomische Formel (2)Die 2. Binomische Formel grafisch in Form von Flächen dargestellt. (a-b)² = a² - 2·a·b + b². Bitte lest euch die Einleitung durch. -
 Binomische Formel (3)Die 3. Binomische Formel (a+b)·(a-b) = a² - b² kann mit diesem Programm entdeckt werden. Bitte die Einleitung durchlesen.
Binomische Formel (3)Die 3. Binomische Formel (a+b)·(a-b) = a² - b² kann mit diesem Programm entdeckt werden. Bitte die Einleitung durchlesen. -
 Binomische Formeln RechnerDieses Programm berechnet euch die erste und zweite Binomische Formel mit Zahlen und Variablen.
Binomische Formeln RechnerDieses Programm berechnet euch die erste und zweite Binomische Formel mit Zahlen und Variablen. -
 Binomische Formeln RechnerHier könnt ihr jede binomische Formel online berechnen lassen. Einfach Werte eingeben und automatisch werden die Ergebnisse angezeigt. Kontrolliert die Lösungen eurer Hausaufgaben.
Binomische Formeln RechnerHier könnt ihr jede binomische Formel online berechnen lassen. Einfach Werte eingeben und automatisch werden die Ergebnisse angezeigt. Kontrolliert die Lösungen eurer Hausaufgaben.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 4 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Wie rechnet man die Binomische Formel mit Variablen, zum Beispiel (4x+3y)²?
- Gibt es noch mehr Möglichkeiten, die binomischen Formeln zu zerlegen?
- Binomische Formel anwenden beim Term (gh - 0,2ik)² (mit Buchstaben)
- 3. Binomische Formel zur Auflösung des Terms (2+x)·(x-3)?
- Forme die Produkte mit Hilfe der Binomischen Formeln in Summen um: (u²-1/2w)²
Finde weitere Fragen und Antworten in der Mathelounge.



