Lektion TRI07: Bogenmaß und Kreiszahl Pi
In allen vorigen Lektionen zur Trigonometrie haben wir stets das Gradmaß benutzt, um unsere Winkel festzulegen. Wir können jedoch auch andere Winkelmaße benutzen.
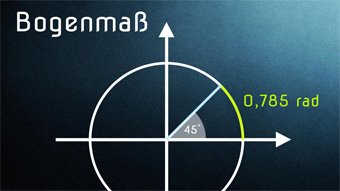
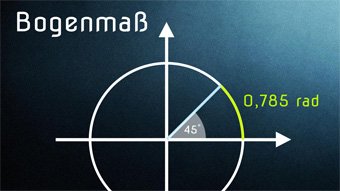
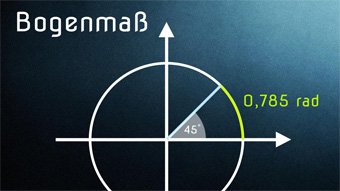
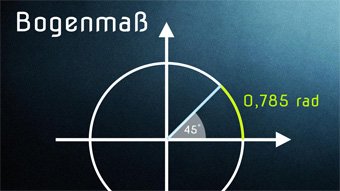
Das Winkelmaß, das am häufigsten in der höhere Mathematik anzutreffen ist, ist das sogenannte Bogenmaß.
In dieser Lektion betrachten wir uns, wie das Bogenmaß definiert ist und was es mit der Kreiszahl Pi zu tun hat.
Weitere Videos für Kunden:
-
TRI07-1 Bogenmaß - EinführungWiederholung der Winkelmaße. Definition von Bogenmaß mit α = Kreisbogen / Kreisradius. Einheit: Radiant. Zusammenhang zwischen Bogenmaß und Kreiszahl Pi.
-
TRI07-2 Bogenmaß - Bogenmaß und Grad umrechnenWie rechnen wir Grad in Bogenmaß um. Wie lässt sich Pi hierzu benutzen? Herleitung der Umrechnungsformeln. Abschließend 2 Aufgaben zur Umrechnung Grad ↔ Bogenmaß.
-
TRI07-3 Bogenmaß - Bogenmaß mit dem TaschenrechnerAuf was müssen wir achten, wenn wir mit dem Taschenrechner Grad und Bogenmaß umrechnen. Taschenrechner-Modi: DEG, RAD, GRAD. Bogenmaß statt Gradmaß beim Sinus: sin(90°) = sin(0,5·Pi) = 1. Bogenmaß bei der Sinusfunktion.
-
TRI07-4 Bogenmaß - Herleitung der Kreiszahl PiWir schauen uns die Kreiszahl Pi näher an: Warum schreibt man Pi? Pi als Verhältnis von Kreisumfang/Kreisdurchmesser. Wir zeigen, wie wir uns dem Pi-Wert von 3,1415... über Polygone (Vielecke) annähern können.
-
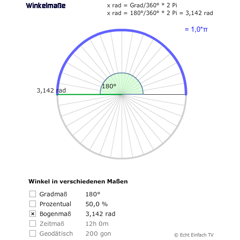 Winkelmaße (Gradmaß, Prozent, Bogenmaß)Verschiedene Winkelmaße (Grad, Prozent, Bogenmaß, Gon, Zeit) zur Veranschaulichung am Kreis.
Winkelmaße (Gradmaß, Prozent, Bogenmaß)Verschiedene Winkelmaße (Grad, Prozent, Bogenmaß, Gon, Zeit) zur Veranschaulichung am Kreis. -
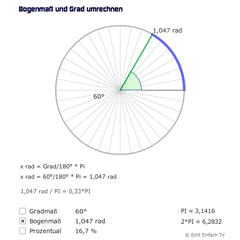 Bogenmaß und Grad umrechnenDieses Programm rechnet euch Grad und Bogenmaß ineinander um, dabei wird der gewählte Winkel am Kreis dargestellt.
Bogenmaß und Grad umrechnenDieses Programm rechnet euch Grad und Bogenmaß ineinander um, dabei wird der gewählte Winkel am Kreis dargestellt. -
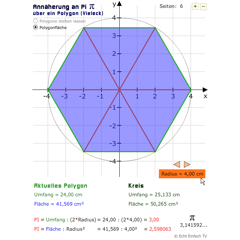 PI - Annäherung über PolygonflächeHier nähern wir uns über die Fläche eines Polygons dem Wert der Kreiszahl Pi an. Mit steigender Seitenanzahl wird der Wert genauer.
PI - Annäherung über PolygonflächeHier nähern wir uns über die Fläche eines Polygons dem Wert der Kreiszahl Pi an. Mit steigender Seitenanzahl wird der Wert genauer. -
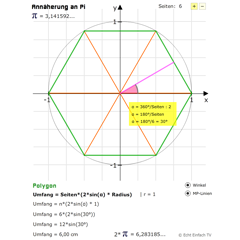 PI - Annäherung über UmfangMit Hilfe des Sinus können wir den Umfang des Polygons berechnen. Mit steigender Seitenanzahl nähern wir uns dem Wert für Pi an.
PI - Annäherung über UmfangMit Hilfe des Sinus können wir den Umfang des Polygons berechnen. Mit steigender Seitenanzahl nähern wir uns dem Wert für Pi an. -
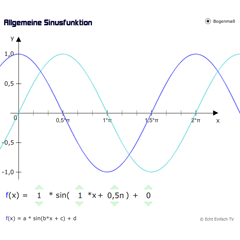 Sinusfunktion (allgemein) mit BogenmaßDie allgemeine Sinusfunktion der Form f(x) = a·sin(b·x + c) + d wird hier dargestellt. Ihr könnt zwischen den Einheiten Grad und Bogenmaß wählen.
Sinusfunktion (allgemein) mit BogenmaßDie allgemeine Sinusfunktion der Form f(x) = a·sin(b·x + c) + d wird hier dargestellt. Ihr könnt zwischen den Einheiten Grad und Bogenmaß wählen.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 4 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
- Wie Grad in Bogenmaß umwandeln?
- Wie Nachkommastellen von Pi selbst berechnen?
- Wird der Radius eines Kreises um 4 cm verlängert, so nimmt der Flächeninhalt um 20π cm² zu.
- Wie berechne ich das Bogenmaß als Vielfaches von Pi?
- Zahlen in Pi angeben (Trigonometrie)
- Fülle die nachstehende Tabelle aus: Grad, Bogenmass
Finde weitere Fragen und Antworten in der Mathelounge.