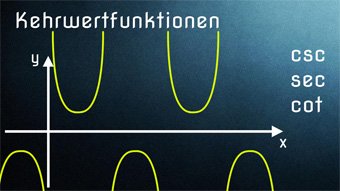
Lektion TRI10: Kehrwertfunktionen (Trigonometrie)
Nachdem wir bereits mehrere Lektionen zur Trigonometrie hinter uns haben, können wir unser Wissen mit den Kehrwertfunktionen abrunden.
Übrigens vermittelt das letzte Video noch einige Einblicke in die höhere Mathematik.
Weitere Videos für Kunden:
-
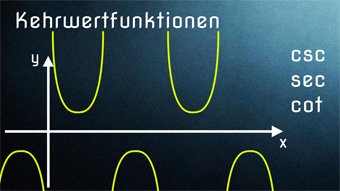
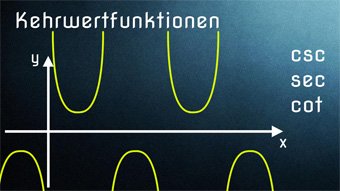
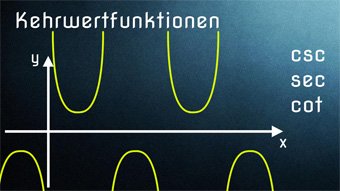
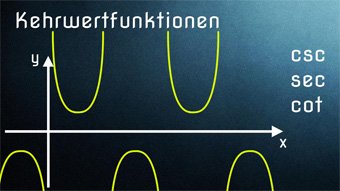
TRI10-1 Kehrwertfunktionen - EinführungWas bedeutet Kehrwert bei der Funktion. Wie sind die Kehrwertfunktionen definiert. Sinus → Kosekans, Kosinus → Sekans, Tangens → Kotangens. Wertebereich (mögliche y-Werte) der Kehrwertfunktionen.
-
TRI10-2 Kehrwertfunktionen - Kosekans u. Sekans am EinheitskreisWir betrachten uns, wie sich die Kehrwertfunktionen Kosekans und Sekans am Einheitskreis ergeben. Klärung der Begriffe Ko-Sekans und Sekans über den Sekantenabschnitt.
-
TRI10-3 Kehrwertfunktionen - Kotangens am EinheitskreisWir schauen uns an, wie Kotangens am Einheitskreis abgelesen wird und weshalb man den Begriff Ko-Tangens verwendet.
-
TRI10-4 Kehrwertfunktionen - Kosekans, Sekans, KotangensWir betrachten die Kosekansfunktion, Sekansfunktion und Kotangensfunktion inklusive Definitionslücken. Beispielaufgabe zum Finden des Schnittpunktes: cot(x-30°) = tan(x-30°).
-
TRI10-5 Ergänzungen zur TrigonometrieBerechnung der Aufgabe sin(x)=cos(x). Was sind gemischt-goniometrische Gleichungen. Blick auf die Umkehrfunktion Arkussinus. Ausdruck des Sinuswertes sin(45°) über eine Wurzel. Rückführung der trigonometrischen Funktionen auf Sinus. Ausblick höhere Mathematik: Taylorreihen + Fourierreihen.
Testet euer Wissen auch mit den Programmen zu den Umkehr- und Kehrwertfunktionen.
-
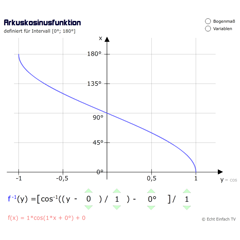 ArkuskosinusfunktionDie Umkehrfunktion für Kosinus ist definiert für das Intervall 0° bis 180°. Sie ordnet einem Kosinuswert den entsprechenden Winkel zu.
ArkuskosinusfunktionDie Umkehrfunktion für Kosinus ist definiert für das Intervall 0° bis 180°. Sie ordnet einem Kosinuswert den entsprechenden Winkel zu. -
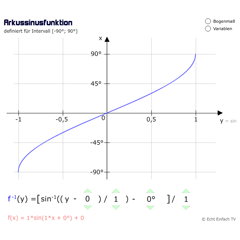 ArkussinusfunktionDie Umkehrfunktion für Sinus ist definiert für das Intervall -90° bis 90°. Sie ordnet einem Sinuswert den entsprechenden Winkel zu.
ArkussinusfunktionDie Umkehrfunktion für Sinus ist definiert für das Intervall -90° bis 90°. Sie ordnet einem Sinuswert den entsprechenden Winkel zu. -
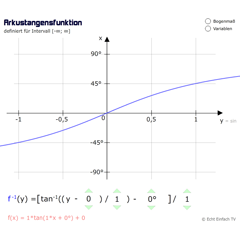 ArkustangensfunktionDie Umkehrfunktion für Tangens ordnet einem Tangenswert den entsprechenden Winkel zu.
ArkustangensfunktionDie Umkehrfunktion für Tangens ordnet einem Tangenswert den entsprechenden Winkel zu. -
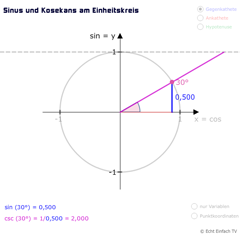 Kosekans am EinheitskreisDie Kehrwertfunktion Kosekans ist definiert als csc(x) = HY/GK = 1/sin(x). Hier wird sie am Einheitskreis veranschaulicht.
Kosekans am EinheitskreisDie Kehrwertfunktion Kosekans ist definiert als csc(x) = HY/GK = 1/sin(x). Hier wird sie am Einheitskreis veranschaulicht. -
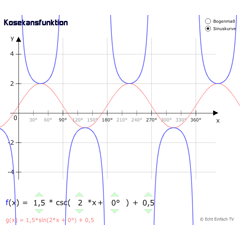 KosekansfunktionDieses Programm zeigt die allgemeine Sinusfunktion sowie die dazugehörige Kehrwertfunktion Kosekans.
KosekansfunktionDieses Programm zeigt die allgemeine Sinusfunktion sowie die dazugehörige Kehrwertfunktion Kosekans. -
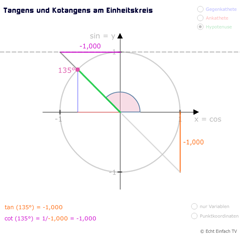 Kotangens am EinheitskreisDie Kehrwertfunktion Kotangens ist definiert als cot(x) = AK/GK = 1/tan(x). Hier wird sie am Einheitskreis veranschaulicht.
Kotangens am EinheitskreisDie Kehrwertfunktion Kotangens ist definiert als cot(x) = AK/GK = 1/tan(x). Hier wird sie am Einheitskreis veranschaulicht. -
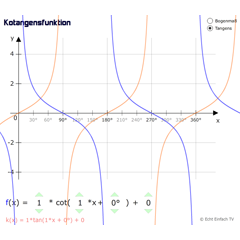 KotangensfunktionDieses Programm zeigt die allgemeine Tangensfunktion sowie die dazugehörige Kehrwertfunktion Kotangens.
KotangensfunktionDieses Programm zeigt die allgemeine Tangensfunktion sowie die dazugehörige Kehrwertfunktion Kotangens. -
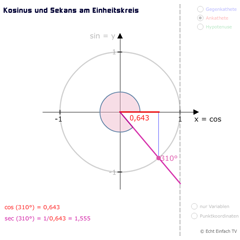 Sekans am EinheitskreisDie Kehrwertfunktion Sekans ist definiert als sec(x) = HY/AK = 1/cos(x). Hier wird sie am Einheitskreis veranschaulicht.
Sekans am EinheitskreisDie Kehrwertfunktion Sekans ist definiert als sec(x) = HY/AK = 1/cos(x). Hier wird sie am Einheitskreis veranschaulicht. -
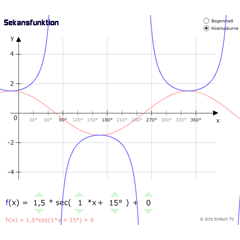 SekansfunktionDieses Programm zeigt die allgemeine Kosinusfunktion sowie die dazugehörige Kehrwertfunktion Sekans.
SekansfunktionDieses Programm zeigt die allgemeine Kosinusfunktion sowie die dazugehörige Kehrwertfunktion Sekans.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Artikel im Wiki:
- Kehrwertfunktionen - Einführung
- Kosekans - Kehrwertfunktion von Sinus
- Sekans - Kehrwertfunktion von Kosinus
- Kotangens - Kehrwertfunktion von Tangens
- Übersicht Kehrwertfunktionen der Trigonometrie
- Kosekans am Einheitskreis
- Sekans am Einheitskreis
- Wortherkunft Sekans und Kosekans
- Kotangens am Einheitskreis
- Wortherkunft Kotangens
- Kosekans als Funktionsgraph
- Sekans als Funktionsgraph
- Kotangens als Funktionsgraph
- Funktion von Arkussinus
- Umkehrfunktion von Sinus herleiten
- Unterschied zwischen Umkehrfunktion und Kehrwertfunktion
Häufige Fragen:
- Steigung einer Funktion (Winkel 35°) mit Tangens ermitteln?
- Ein 32 m großer Turm ist 64 m vom Ufer eines Flusses entfernt. Wie breit ist der Fluss?
- Berechnung von Seiten und Winkeln mit Sinus, Kosinus und Tangens
- Bestimme die Länge x aus einer Gleichung mit Tangens (alle Maße in cm)?
- Die Sonne sieht man unter einem Sehwinkel von 32'. Welchen Durchmesser besitzt die Sonne ungefähr?
- Trigonometrie: Steigung und Steigungswinkel bei Reibungsbahnen und Standseilbahnen.
- Trigonometrie in einem Kegel: Berechne den Neigungswinkel, die Höhe und die Oberfläche des Daches.
Finde weitere Fragen und Antworten in der Mathelounge.