AB: Lektion Flächenberechnung mittels Integral I
Nachfolgend findet ihr Aufgaben zur Flächenberechnung mittels Integralen, mit denen ihr euer Wissen testen könnt.
Bestimme die Fläche zwischen Graphen und x-Achse:
Um den Flächeninhalt zu berechnen ist es oft hilfreich eine Skizze zu machen. Das machen wir hier immer als ersten Schritt und arbeiten uns dann mit dieser visuellen Stütze zum Ergebnis durch.
\( f(x) = x^2 -3 \)
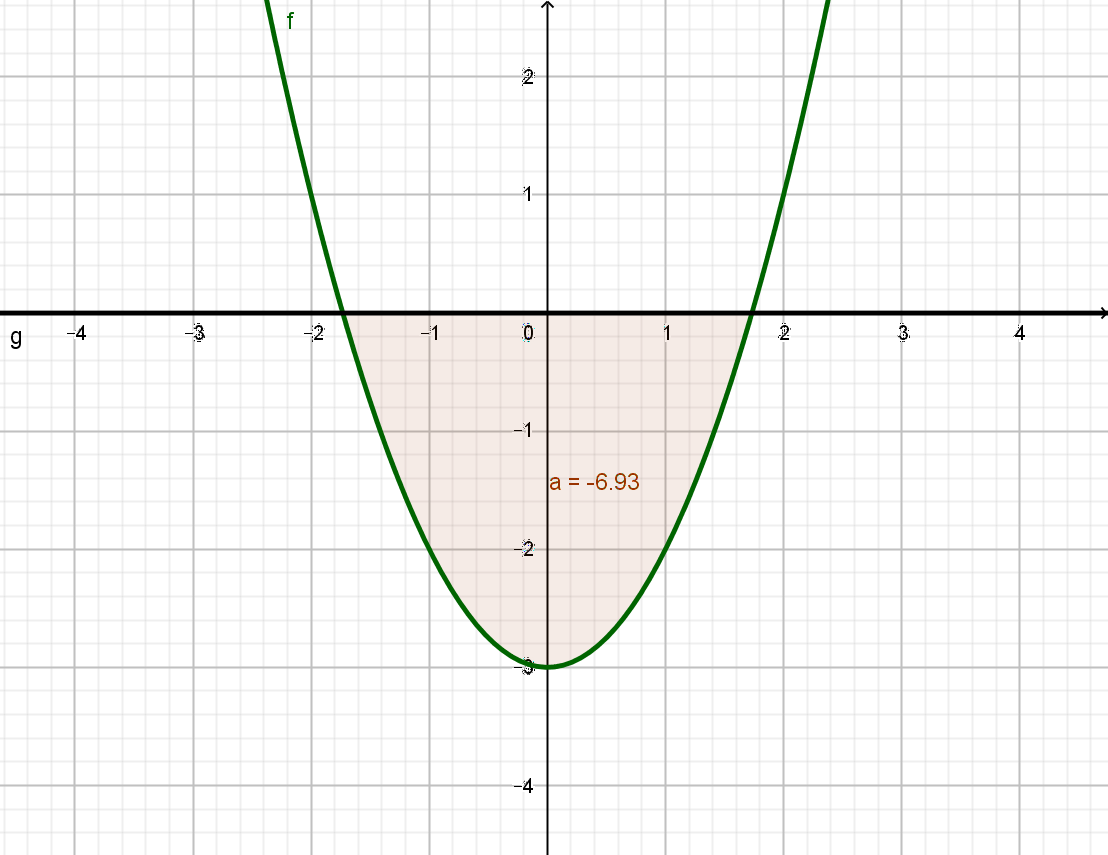
Wie wir sehen und uns erinnern, sind zur Bestimmung des Flächeninhalts zwischen der Funktion f und der x-Achse, die Nullstellen zu berechnen. Erst dann hat man die Grenzen und kann die Fläche über das Integral bestimmen.
\( x^2 - 3 = 0 \\ x^2 = 3 \\ x_{1,2} = \pm \sqrt{3} \)
Demnach haben wir die Integralgrenzen bestimmt zu \( -\sqrt{3} \) und \( \sqrt{3} \).
Zur Berechnung des Flächeninhalts:
\( \int \limits_{-\sqrt{3} }^{\sqrt{3} } x^2-3 \; dx = \left[\frac{1}{3}x^3-3x\right]_{-\sqrt{3} }^{ \sqrt{3} } \\ =\frac{1}{3}(\sqrt{3} )^3-3\sqrt{3} - \left(\frac{1}{3}(-\sqrt{3} )^3 - 3(-\sqrt{3} )\right) \approx -6,93 \)
Nun müssen wir noch den Betrag nehmen, da Flächen ja stets positiv sind. Der gesuchte Flächeninhalt ist also etwa A = 6,93 FE (FE = Flächeneinheiten).
Alternativ hätten wir auch die Symmetrie ausnutzen können. Wir hatten ja gesagt, dass bei der Achsensymmetrie die eine Hälfte errechnet wird, und dann das ganze mit 2 multipliziert wird.
\( 2\int \limits_{0}^{\sqrt{3} } x^2-3 \; dx = 2\left[\frac{1}{3}x^3-3x\right]_{0}^{\sqrt{3} } \\ =2\left(\frac{1}{3}(\sqrt{3} )^3 - 3\sqrt{3} - 0\right) \approx -6,93 \)
\( g(x) = -x^2 + 3 \)
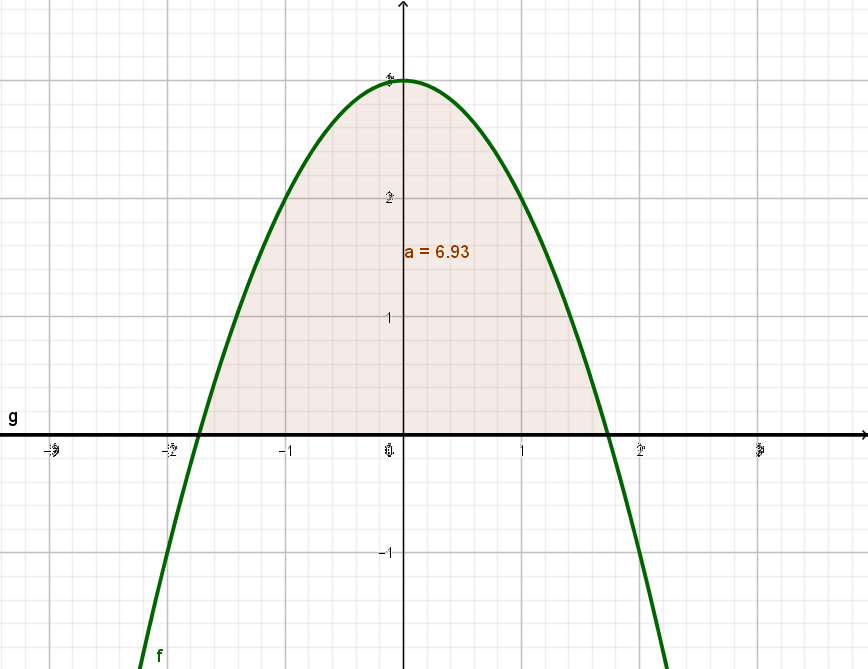
Spätestens mit der Skizze fällt sofort auf, dass hier der Funktionsgraph nur an der x-Achse gespiegelt wurde. Die Rechnung ist also identisch wie bei a). Nur muss hier am Ende nicht auf den Betrag geachtet werden, da die Fläche ohnehin schon positiv ist.
\( h(x) = x^3 - 3·x^2 - x + 3 \)
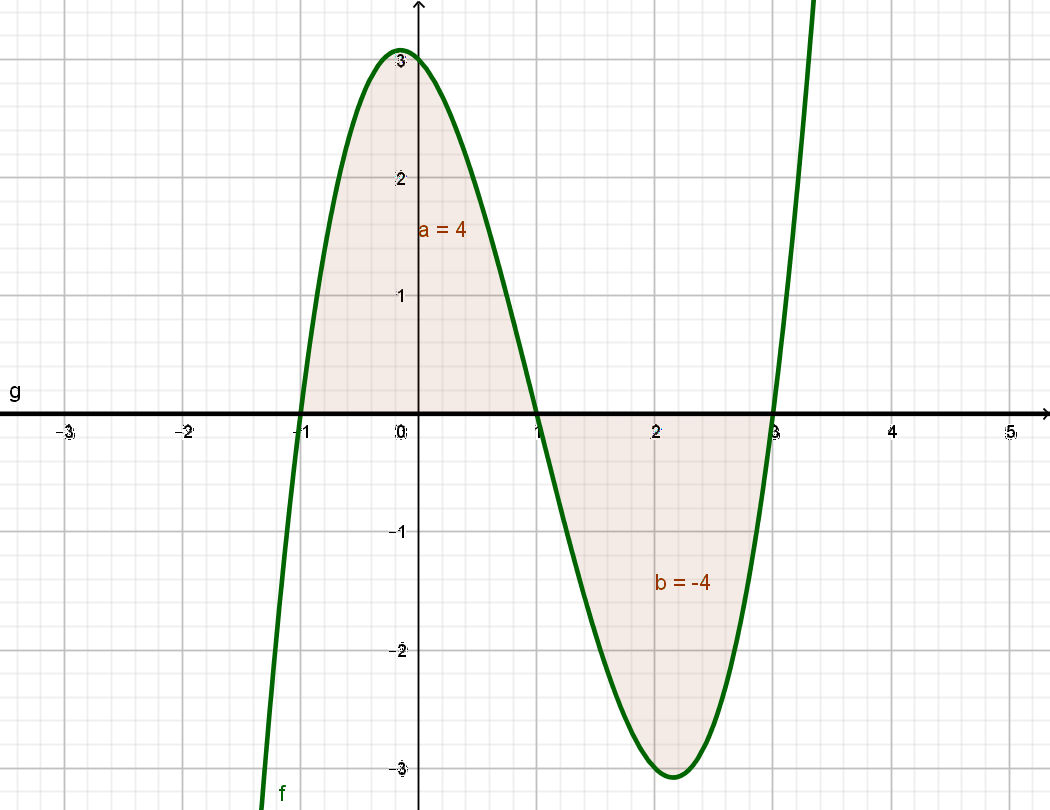
Auch hier sind wieder die Nullstellen zu suchen. Bei der Nullstellensuche nutzt man am besten die Polynomdivision, indem man einen Nullstelle errät. Mit x = 3 findet man eine Nullstelle.
(x³ - 3·x² - x + 3) : (x - 3) = x² - 1
x^3 - 3x^2
————————
- x + 3
- x + 3
————————
0
Über die obere Gleichung zweiten Grades findet man die beiden anderen Nullstellen x = -1 und x = 1 (entweder über binomische Formel, oder x²-1 = 0 → x² = 1 → x1,2 = ±1). Wir müssen also diesmal zwei Integrale lösen um den Gesamtflächeninhalt zu erhalten. Die Einsetzschritte seien hier mal übersprungen.
\( \int \limits_{-1}^1 x^3-3x^2-x+3 \; dx = \left[\frac{1}{4}x^4-x^3-\frac{1}{2}x^2+3x\right]_{-1}^1 = 4 \\ \int \limits_1^3 x^3-3x^2-x+3 \; dx = \left[\frac{1}{4}x^4-x^3-\frac{1}{2}x^2+3x\right]_{1}^3 = -4 \)
Nun beide Flächen betragsmäßig addieren: 4 + |-4| = 4 + 4 = 8. Der Flächeninhalt beträgt also 8 FE.
\( k(x) = (x - 2)·\ln(x) \)
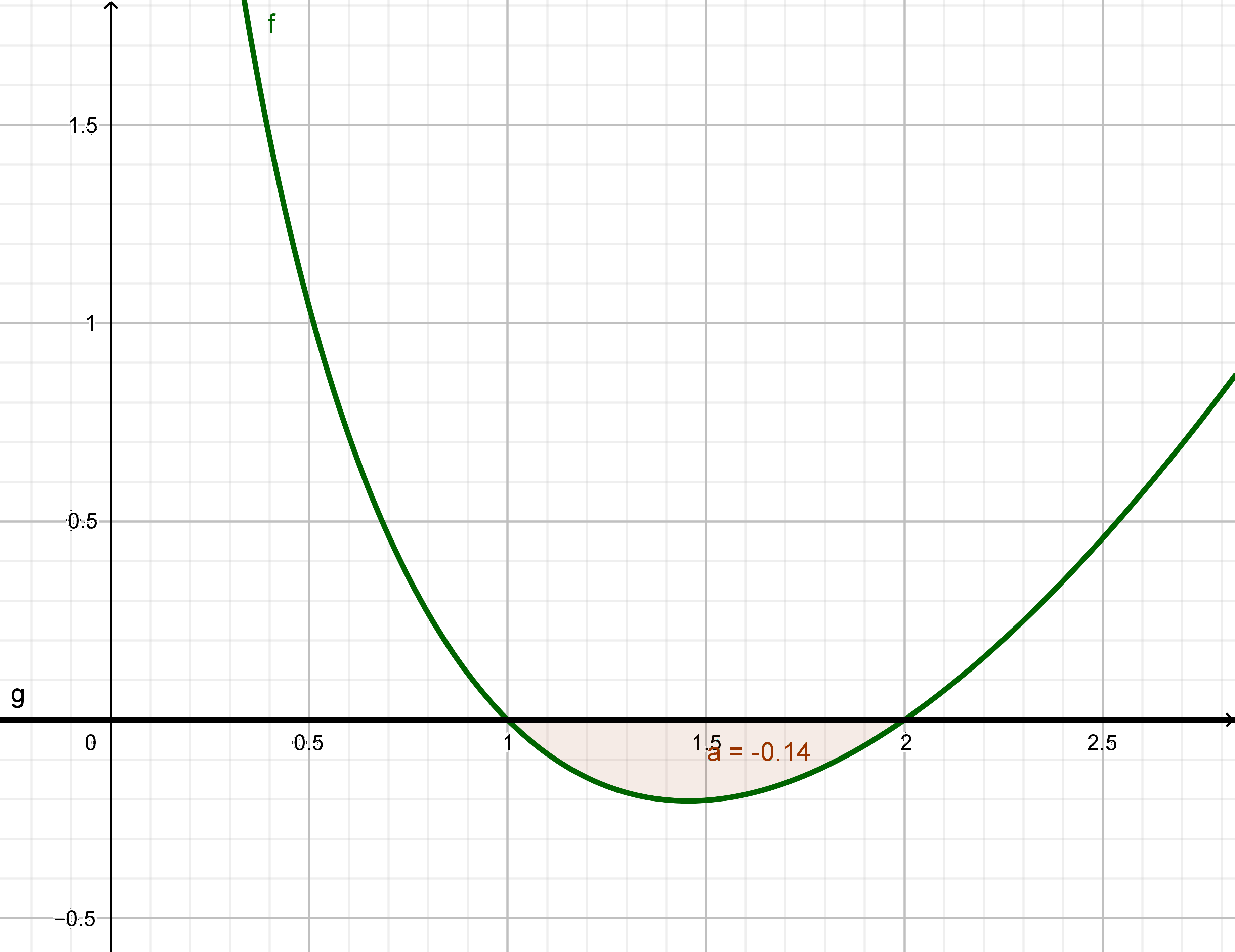
Die Nullstellen kann man direkt ablesen, wenn man weiß, dass der Logarithmus für x = 1 den Wert 0 annimmt. Dann sind die Nullstellen x = 1 und x = 2. Mit der gerade behandelten partiellen Integration können wir das lösen.
u = ln(x) und v’ = x - 2, also u’ = \( \frac{1}{x} \) und v = 1
\( \int \limits_1^{2} (x-2)\cdot \ln(x)\; dx = \int \limits_1^2 x\ln(x) \; dx - 2\int \limits_1^2 \ln(x) \;dx \)
Sowohl das erste als auch letzte Integral haben wir in der letzten Lektion schon kennengelernt (siehe Aufgaben 1 und 2 in 7C). Man kommt damit auf:
\( \left[-\frac{1}{4}x^2+\frac{1}{2}x^2\ln(x)-2x\ln(x) + 2x\right]_1^2 \approx -0,14 \)
Das müssen wir nun noch im Betrag betrachten und haben dann einen Flächeninhalt von etwa 0,14 FE.
\( m(x) = x^2·(x - 2) \)
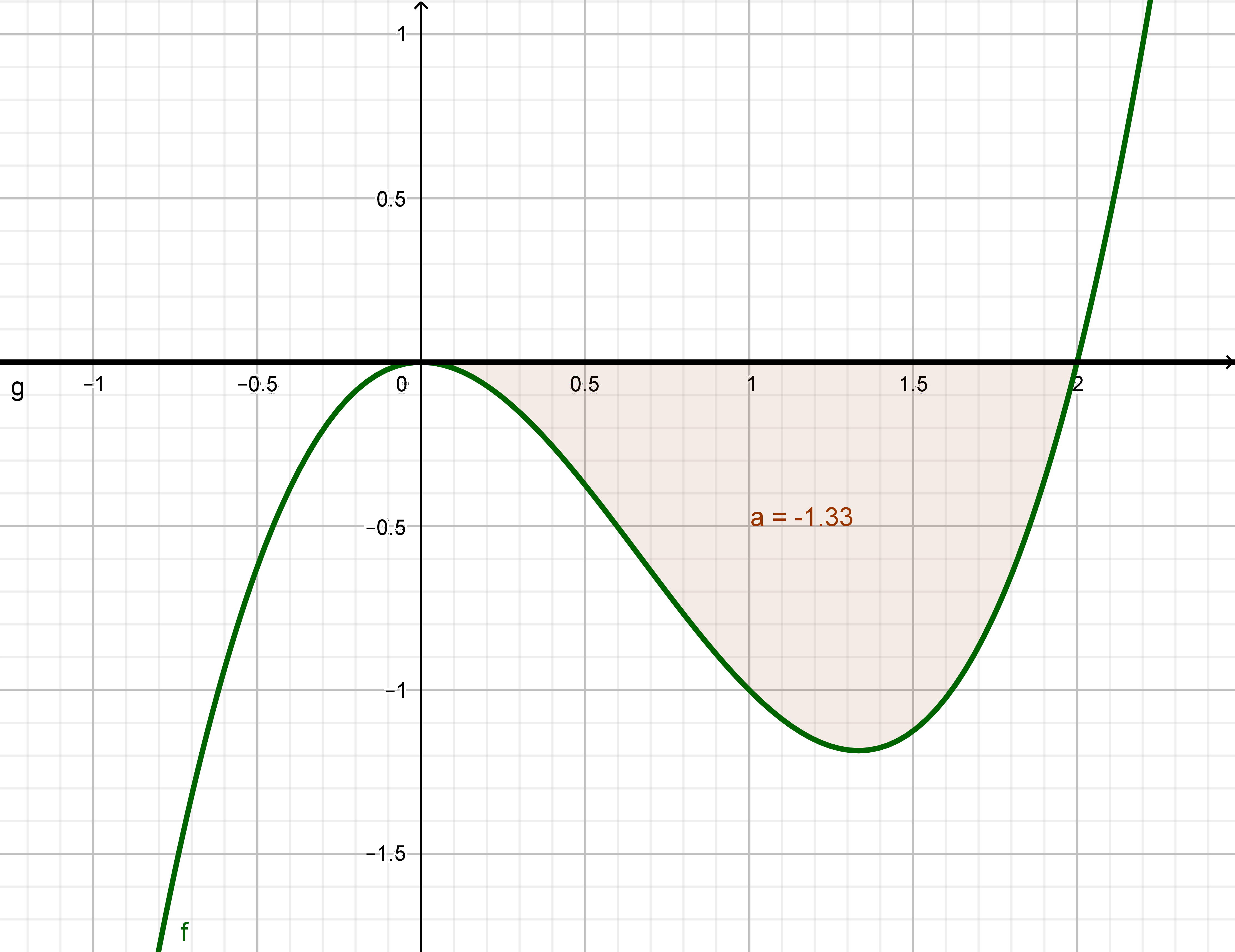
Hier können wir wieder die Nullstellen direkt zu x = 0 und x = 2 ablesen. So auch das Integral aufstellen:
\( \int \limits_0^2 x^2\cdot(x-2) \;dx = \int \limits_0^2 x^3-2x^2 \; dx = \left[\frac{1}{4}x^4-\frac{2}{3}x^3\right]_0^2 = -\frac{4}{3} \)
Der Flächeninhalt ist demnach \( \frac{4}{3} \) FE.
