AB: Satz des Pythagoras und verwandte Sätze (1)
Satz des Pythagoras:
Sind a und b die Katheten eines rechtwinkligen Dreiecks mit der Hypotenuse c, dann gilt a² + b² = c².
Höhensatz des Euklid:
Der Fußpunkt H der Höhe h auf der Hypotenuse c teilt c in zwei Hypotenusenabschnitte p und q und es gilt: h²=p·q.
Kathetensatz des Euklid:
Sei a eine Kathete eines rechtwinkligen Dreiecks mit der Hypotenuse c und p derjenige Hypotenusenabschnitt,
der eine gemeinsamen Punkt mit a hat, dann gilt a² = p·c.
Rechtwinklige Dreiecke im Quadrat: Gegeben ist ein Dreieck ABC mit den Seitenlängen a = √13 cm, b = √17 cm und c = √20 cm.
Zeigen Sie, dass sich die Punkte A, B und C auf den Seiten eines Quadrates mit der Seitenlänge 4 cm anordnen lassen.
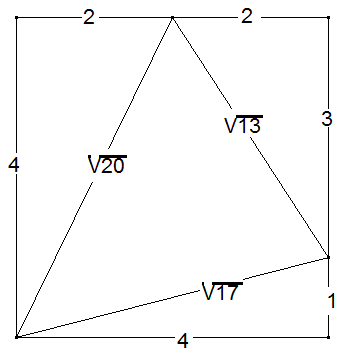
Berechnen Sie auf der Basis bisheriger Ergebnisse den Flächeninhalt des Dreiecks ABC.
16 – 3 – 4 – 2 = 7
Fast Pythagoras: Das Dreieck ABC ist nicht rechtwinklig. Das Lot von C auf AB teilt AB in die Abschnitte p und q. ADEB ist ein Quadrat.
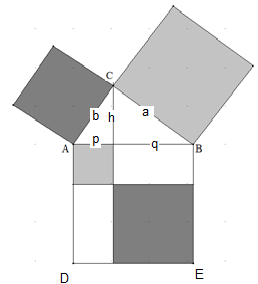
Zeigen Sie: Die hellgrau unterlegten Quadrate haben zusammen den gleichen Flächeninhalt wie die dunkelgrau unterlegten Quadrate zusammen.
Nach Pythagoras gilt:
(1) h² + p² = b²
und
(2) h² + q² = a².
(1) – (2) ergibt p² – q² = b² – a² oder p² + a² = b² + q².
Inkreismittelpunkt
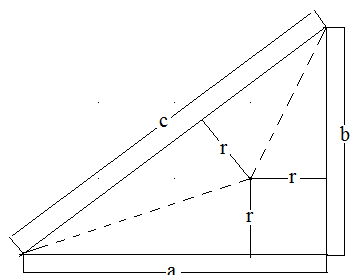
Zeigen Sie: Für den Inkreisradius r im rechtwinkligen Dreieck gilt \( r = \frac{1}{2} (a+b-c) \). Verwenden Sie Skizze.
Der Mittelpunkt des In-kreises ist der Schnittpunkt der Winkelhalbierenden. Daher lässt sich aus neben-stehender Skizze c = a – r + b – r ablesen. Auflösen nach r ergibt r = ½ (a+b-c).
Zeigen Sie: Für den Inkreisradius r im rechtwinkligen Dreieck gilt \( r = \frac{ {ab} }{ {a + b + c} } \).
r sei jeweils Höhe in den drei Dreiecken mit a, b und c als Grundseiten: Dann gilt \( \frac{ {ar} }{2} + \frac{ {br} }{2} + \frac{ {cr} }{2} = \frac{ {ab} }{2} \). Auflösen nach r ergibt r = \( \frac{ {ab} }{ {a + b + c} } \).
Beweisen Sie mit Hilfe der Gleichungen aus a) und b) den Satz des Pythagoras.
Gleichsetzen der Ergebnisse aus a) und b) führt zu \( \frac{ {ab} }{ {a + b + c} } = \frac{ {a + b - c} }{2} \). Durchmultiplizieren mit dem Hauptnenner ergibt 2ab = ((a+b) – c)·((a+b)+c)=(a+b)² – c² und schließlich a²+b²=c².
Zwei Kreise: Die Mittelpunkte zweier Kreise und ihr Berührpunkt B liegen auf einer Geraden g. M sei der Mittelpunkt des größeren Kreises. Die Senkrechte auf g in M sei h. Der Abstand zwischen den Kreisen auf g ist 9 cm, der Abstand zwischen den Kreisen auf h ist in beiden Fällen 5 cm (siehe Abbildung).
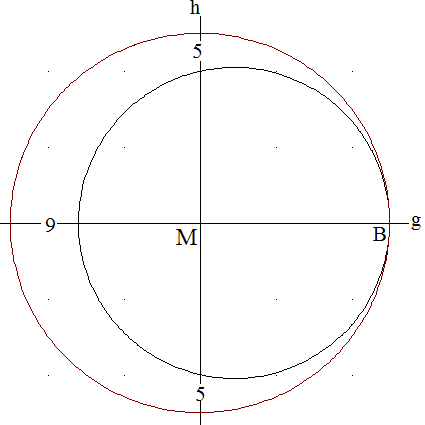
Wie groß sind die Radien der Kreise?
Führen Sie diese Hilfslinien und Bezeichnungen ein: Dann ist (1) h² = p · q und p + 9 = q sowie (3) h = q - 5. Das sind drei Gleichungen mit drei Unbekannten. Lösungen: p = 16, q = 25 und h = 20.
