AB: Regelmäßige n-Ecke und n,k-Sterne (3)
Zwölfeck: A, B, C, D seien die Seitenmitten eines Quadrats und gleichzeitig vier Eck-punkte eines regelmäßigen Zwölfecks. Der wievielte Teil der Quadratfläche wird von der Fläche des Zwölfecks bedeckt?
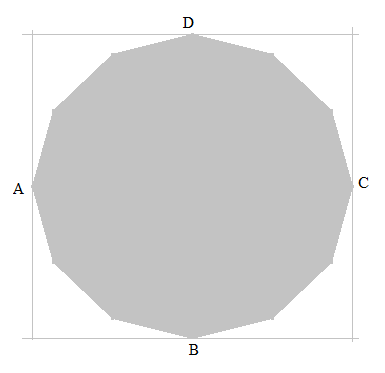
In der Formelsammlung findet man: Für den Flächeninhalt F eines Zwölfecks mit dem Umkreisradius r gilt F = 3r². Das Quadrat mit der Seitenlänge 2r hat den Flächeninhalt 4r².
Nochmal: Flächenvergleich Zwölfeck/Quadrat ABCDEFG ist ein Polygonzug, der ein Viertel eines 12,5-Sterns begrenzt.
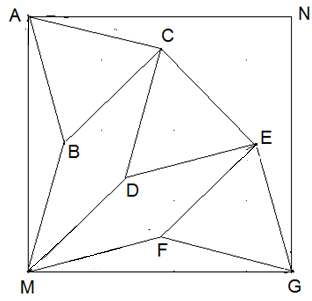
Bestimmen Sie die Größen der Winkel ACE und BCD. Begründen sie dann, dass ABC ein gleichseitiges Dreieck ist.
Winkel ACE ist Innenwinkel eines regelmäßigen Zwölfecks und daher \( \frac{(12-2)·180°}{6} = 150° \). Winkel BCD. Ist Zackenwinkel eines 12,5-Sterns und folglich \( \frac{180°·(12-2·5)}{6} = 150° \). Dann ist der Winkel BCA 60° und dann auch der Winkel BAC. Die Schenkel BA und BC sind gleichlang. Daher ist ABC ein gleichseitiges Dreieck.
Bestimmen Sie alle Winkel im Viereck MDCB und begründen Sie u.a. damit, dass es eine Raute ist.
Der Winkel FMG ist die Hälfte von 30° und ein Sechstel von 90°. Folglich ist MGF ein gleichseitiges Dreieck und daher sind alle Strecken im Inneren des Quadrats MGNA gleichlang. Das Viereck MDCB ist eine Raute.
Bestimmen Sie das Flächenverhältnis des Dreiecks MGE zum Quadrat MGNA?
Das Dreieck MGE ist aus zwei kongruenten gleichschenkligen und einem gleichseitigen Dreieck zusammengesetzt. Das Quadrat MGNA enthält acht kongruente gleichschenklige und vier kongruente gleichseitige Dreiecke. Also hat das Quadrat MGNA den vierfachen Flächeninhalt des Dreiecks MGE.
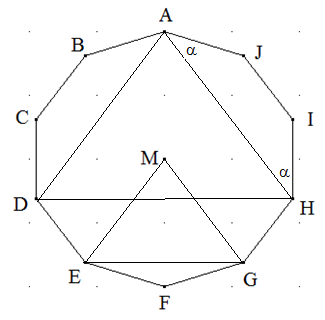
Regelmäßiges Zehneck: Einem regelmäßigen Zehneck ABCDEFGHIJ mit dem Umkreismittelpunkt M seien die Dreiecke ADH und MEG einbeschrieben. Zeigen Sie, dass die Dreiecke ADH und MEG ähnlich sind.
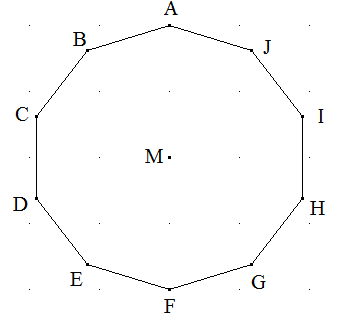
Jeder Innenwinkel des Zehnecks ist \( \frac{(10-2)·180°}{10} = 144° \). Im Viereck AHIJ gilt: 2·α + 288° = 360° und daher α=36°. Das Gleiche gilt für den Winkel DAB. Dann berechnet sich der Winkel DAH als 144° - 2⋅36°=72°. Die Dreiecke DHA und EGM sind gleichschenklig. Der Winkel EMG ist ein Fünftel des Vollwinkels und daher 72° groß. Gleichschenklige Dreiecke mit dem gleichen Winkel gegenüber der Basis sind ähnlich.
Die 8,2-Sterne: Zwei 8,2-Sterne sind so zerschnitten, wie die Abbildung auf der nächsten Seite zeigt. Legen Sie die Teile zu einem 8,2-Stern mit dem doppelten Flächeninhalt zusammen.