AB: Regelmäßige n-Ecke und n,k-Sterne (4)
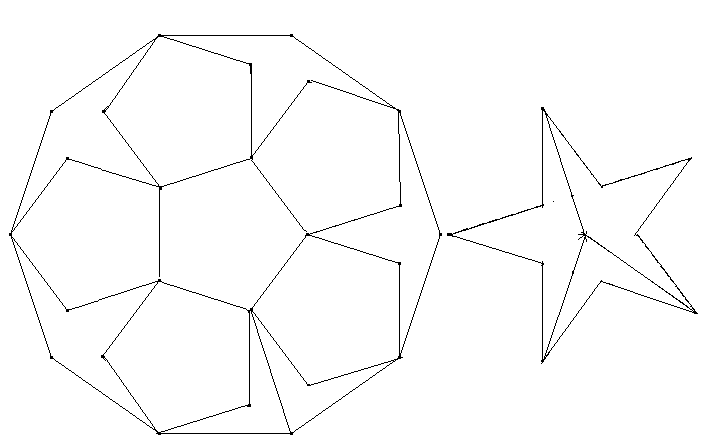
Der 10,4-Stern: Die Zacken eines 10,4-Sterns werden wie dargestellt abgeschnitten und in veränderter Lage an das verbliebene 10-Eck angesetzt, sodass ein neuer n,k-Stern entsteht. Welche Bezeichnung hat dieser Stern (n=?, k=?)?
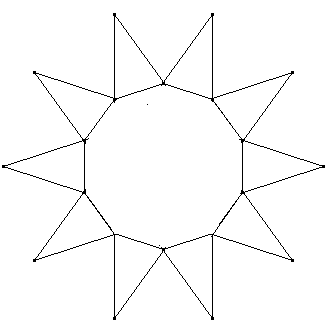
Die abgeschnittenen Zacken sind gleichschenklige Dreiecke. Da ein 10,4-Stern aus zwei 5,2-Sternen zusammengesetzt ist, hat der Zackenwinkel die Größe \( \frac{180°·(5-2·2)}{5} = 36° \). Dann sind die Basiswinkel der abgechnittenen Dreiecke je 72° groß. Diese werden in obiger Figur zu Zackenwinkeln des neuen 10,k-Sterns. Darin gilt für k \( 72° = \frac{ {180° · (10 - 2k)} }{10} \). Aufgelöst nach k ergibt das k=3. Es ist also ein 10,3-Stern.
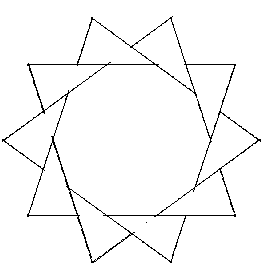
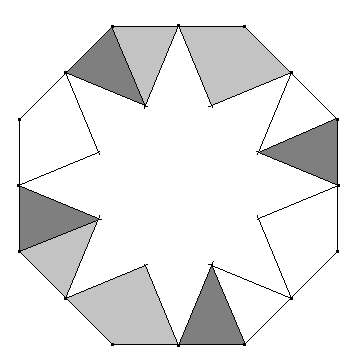
Zwei 8,3-Sterne: Einer von zwei 8,3-Sternen wird in 12 Teile zerschnitten. Mit diesen 12 Teilen sowie einem weiteren 8,3-Stern soll ein regelmäßiges Achteck ausgelegt werden.
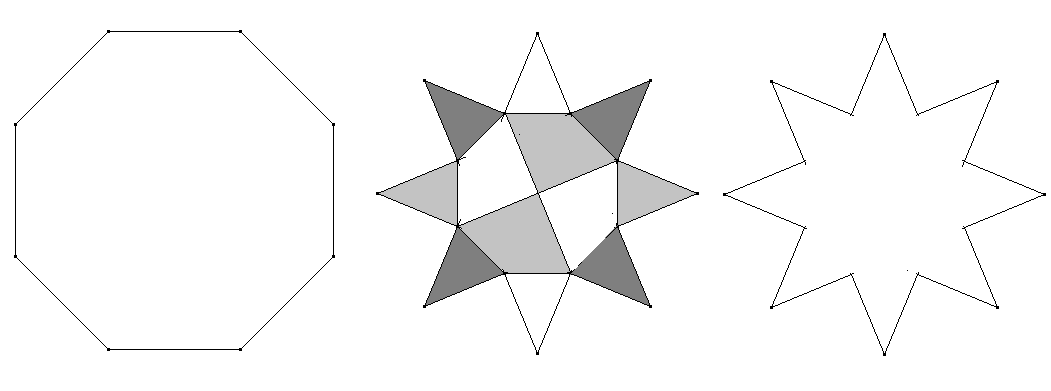
Hier die Auslegung:
Ptolemäus und Fünfeck: Der Satz des Ptolemäus lautet: In einem Sehnenviereck ist das Produkt der Längen der Diagonalen gleich der Summe der Produkte der Längen gegenüberliegender Seiten. Beweisen Sie damit den Satz; Im regelmäßigen Fünfeck ist das Verhältnis aus Diagonalenlänge und Seitenlänge \( \frac{ {1 + \sqrt 5 } }{2} \).
Ein regelmäßiges Fünfeck besteht aus einem gleichschenkligen Trapez und einem gleichschenkligen Dreieck. Die Diagonalen des regelmäßigen Fünfecks sind auch Diagonalen des Trapezes, das auch Sehnenviereck ist. Für die Seitenlänge s und die Diagonalenlänge d des regelmäßigen Fünfecks gilt nach Ptolemaios: sd+s²=d². Nach Division durch d² ergibt sich: \(\frac{s}{d} + {\left( {\frac{s}{d} } \right)^2} = 1\). Nach Substitution von \(\frac{s}{d} = x\) entsteht die quadratische Gleichung x + x² = 1 mit den Lösungen \( x_{1,2} = -0,5 ± \sqrt{1,25} \), also \( x_1 ≈ 0,61803 \text{ und } x_2 ≈ -1,61803 \). Die negative Lösung entfällt hier.
5,2-Sterne und regelmäßige Fünfecke: Zwei 5,2-Sterne und sechs regelmäßige Fünfecke gleicher Seitenlängen sollen zu einem regelmäßigen 10-Eck zusammengesetzt werden. Dazu müssen die 5,2-Sterne zerschnitten werden.
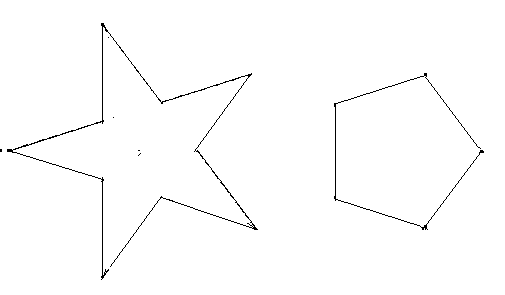
Ein Hinweis auf die Lösung: