AB: Flächengleichheit/Puzzles (1)

Roland Schröder

Einführung Flächengleichheit/Puzzles:

Zwei Flächenmaße lassen sich besonders gut als gleichgroß erkennen, wenn man beide Flächen in paarweise kongruente, überschneidungsfreie Teilflächen zerlegen kann. Die angegebenen Lösungen enthalten oft nur Plausibilitäten. Exakte mathematische Beweise würden den Nachweis der Kongruenz entsprechender Teilflächen erfordern, auf den aber verzichtet wird.

1.

Quadrat mit 5 Quadraten ausgelegt: Die grau unterlegten Quadrate haben die Seitenlange 1 LE. Sie sind also Flächeneinheiten (FE).

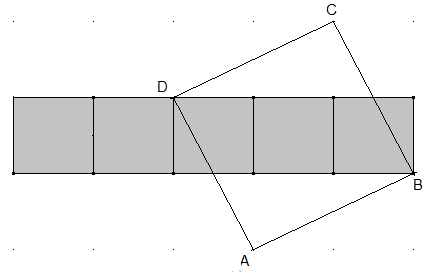
Abbildung: Quadrat mit 5 Quadraten

a)

Zeigen Sie durch Anwendung des Satzes von Pythagoras: Das Quadrat ABCD ist flächengleich zur grau unterlegten Gesamtfläche.

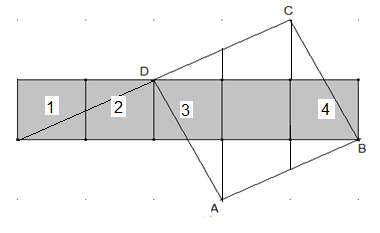
Abbildung: Lösung Quadrat mit 5 Quadraten

b)

Zerschneiden Sie vier der grau unterlegten Quadrate mit je einem geraden Schnitt so, dass das Quadrat ABCD mit den Teilstücken ausgelegt werden kann.

Abbildung: Lösung Quadrat mit 5 Quadraten

2.

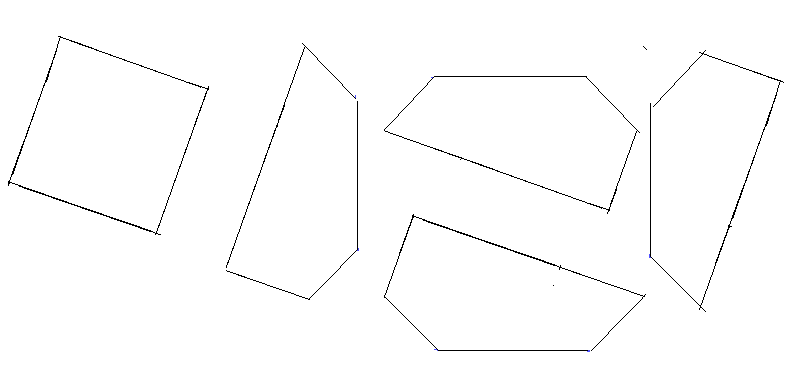
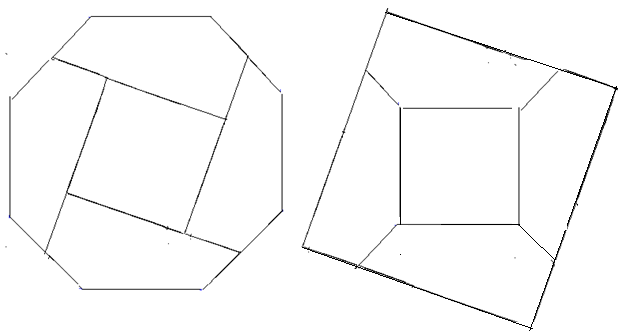
Achteck und Quadrat: Aus den fünf Teilen soll wahlweise ein regelmäßiges Achteck oder ein Quadrat zusammengelegt werden.

Abbildung: Achteck und Quadrat

Abbildung: Lösung Achteck und Quadrat

3.

Gleichseitige Dreiecke: Ein gleichseitiges Dreieck wird in 6 Teile zerschnitten, wie in der Abbildung dargestellt.

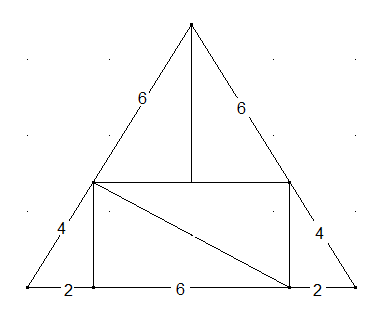
Abbildung: Gleichseitige Dreiecke

a)

Setzen Sie unter Verwendung aller sechs Teile 3 verschiedene gleichseitige Dreiecke zusammen. Welchen Flächenanteil am gesamten Dreieck hat jedes dieser zusammengesetzten gleichseitigen Dreiecke?

Flächenanteile vom Ausgangsdreieck.

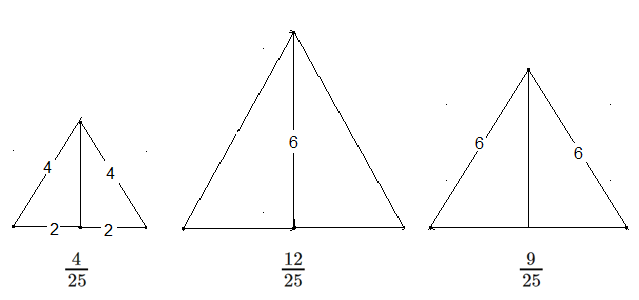
Abbildung: Lösung A – Gleichseitige Dreiecke

b)

Setzen Sie aus diesen 6 Teilen unter Verwendung aller sechs Teile 2 verschiedene gleichseitige Dreiecke zusammen. Welchen Flächenanteil am gesamten Dreieck hat jedes dieser zusammengesetzten gleichseitigen Dreiecke?

Flächenanteile vom Ausgangsdreieck.

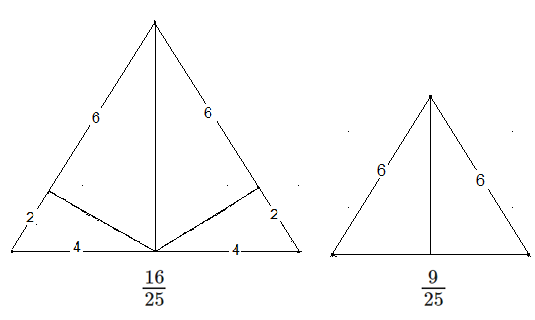
Abbildung: Lösung B – Gleichseitige Dreiecke

\(\frac{16}{25} \) \(\frac{9}{25}\)

4.

Schattenriss einer Bischofsmütze: Aus einem Quadrat mit der Seiten-länge 8 wird ein Viertel seiner Fläche herausgeschnitten. Die Schnittlinien verlaufen von zwei benachbarten Eckpunkten zum Diagonalenschnittpunkt M (linke Skizze, Schattenriss einer Bischofsmütze). Die verbliebene Fläche wird in fünf Stücke – wie dargestellt – zerschnitten. Damit soll das Quadrat ausgelegt werden.

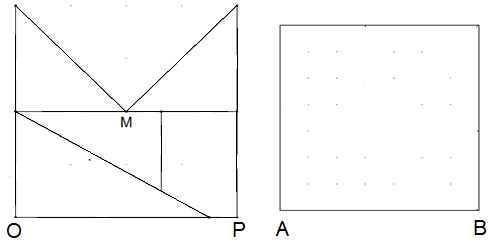
Abbildung: Schattenriss einer Bischofsmütze

a)

Führen Sie die Auslegung durch.

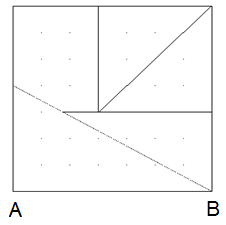
Abbildung: Lösung A - Schattenriss einer Bischofsmütze

b)

Wie lang ist eine Seite AB des Quadrats?

Die Seitenlänge AB ist \(\sqrt {64 - 16} = \sqrt {48} \)

Lösungen

Name:  
Datum: