AB: Flächengleichheit/Puzzles (5)
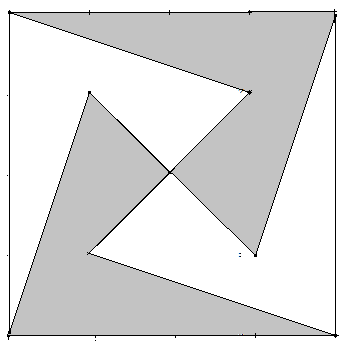
Regelmäßiges Sechseck zerlegen: Zerlegen Sie mit zwei geraden Schnitten ein regelmäßiges Sechseck so in drei flächengleiche Teile, dass beide Schnitte:
durch den gleichen Eckpunkt gehen.
Die Schnitte gehen durch die Ecke C des Sechsecks sowie durch zwei Seitenmitten M und N (siehe Abbildung). Ein regelmäßiges Sechseck mit der Seitenlänge 1 hat den Flächeninhalt \( F = \frac{ {3\sqrt{3} } }{2}\). Die Fläche A1 berechnet sich am einfachsten als \( A_1 = \frac{ { {\rm{sin} }\left( {120^\circ } \right)} }{2} = \frac{ {\sqrt{3} } }{4}\). Fläche A2 ist die Fläche eines rechtwinkligen Dreiecks mit den Kathetenlängen √3 und \(\frac{1}{2}\), sodass \( A_2 = \frac{ {\sqrt{3} } }{4}\). Aus Symmetriegründen ist dann \( A_3 = \frac{ {\sqrt{3} } }{2}\) und \( A_4 = \frac{ {3\sqrt{3} } }{2} - \frac{ {\sqrt{3} } }{2} - \frac{ {\sqrt{3} } }{2} = \frac{ {\sqrt{3} } }{2} \).
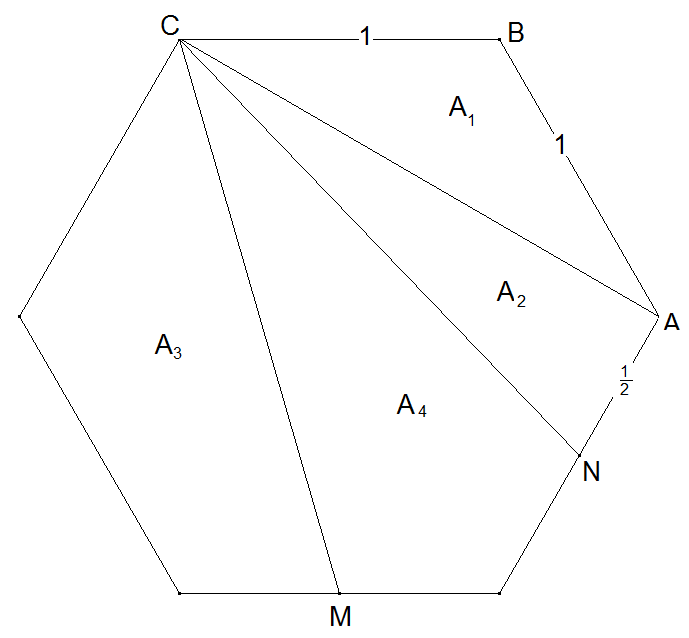
durch die gleiche Seitenmitte gehen.
Die Schnitte gehen durch die Seitenmitte M sowie durch die Eckpunkte des Sechsecks C und B (siehe Abbildung). Die Flächen berechnen sich wie unter a).
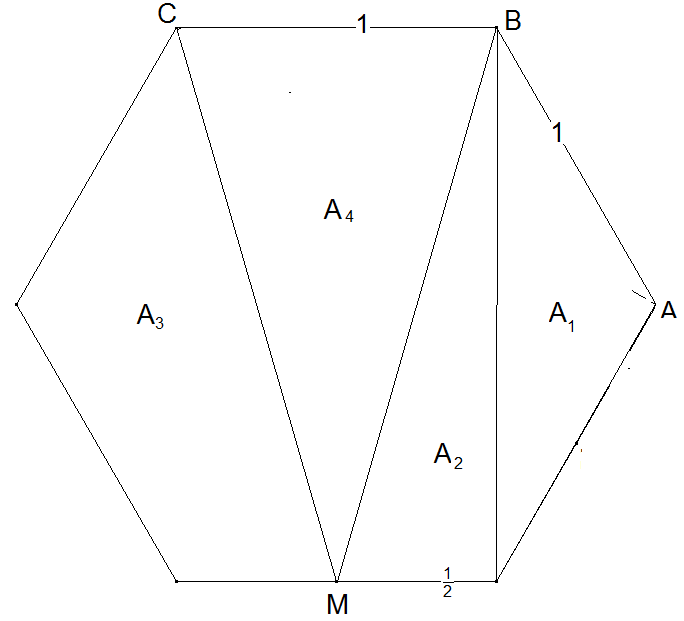
Dreieck zerlegen: Zerlegen Sie mit möglichst wenigen Schnitten ein Dreieck mit den Seitenverhältnissen 6:8:13 in ein flächengleiches Rechteck, dessen eine Seite auf der gleichen Geraden liegt, wie die kürzeste Dreiecksseite.
Senkrechte Seiten des Rechtecks durch zwei Seitenmitten.
Flächengleiche Quadrate: Ein gleichschenkliges Dreieck mit der Schenkellänge a habe den Winkel der Größe 120° zwischen den Schenkeln. Zeigen Sie: Das Quadrat über der Basis ist flächengleich zu 3 Quadraten über dem Schenkel.
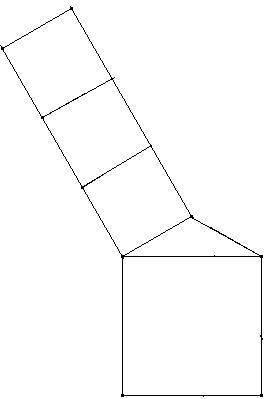
Die Länge der Basis eines gleichschenkligen Dreiecks mit der Seitenlänge a und dem Winkel der Größe 120° gegenüber der Basis ist a·√3. Dann ist die Fläche des Quadrats über der Basis 3a² bzw. a·3a.
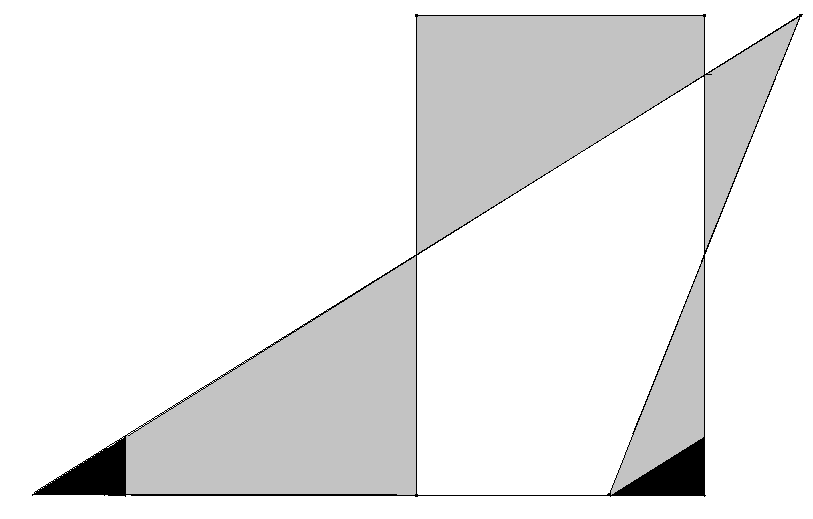
Geschlossener Polygonzug: Der Polygonzug ABCDEA mit A(0|2), B(2|4), C(4|2),D(6|8) und E(6|0) umschließt eine Fläche F.
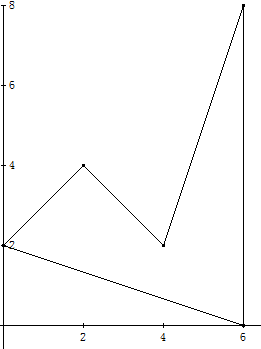
Wie groß ist die Fläche F?
Fläche der Trapeze vermindert um die Fläche des Dreiecks (siehe Bild): (2+4)+(4+2)+(2+8) – 6 =16.
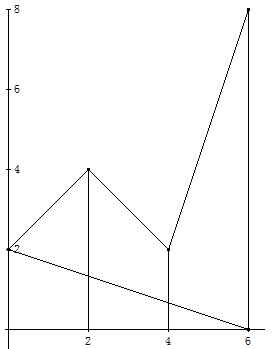
Zeigen Sie durch eine Skizze: Vier kongruente Flächenstücke F lassen sich zu einem Quadrat zusammensetzen. Kontrollieren Sie so das Ergebnis unter a).
Flächenkontrolle 4·16=8·8.