AB: Satz des Pythagoras und verwandte Sätze (2)
Schustermesser: Die linke graue Fläche hat die Form der Klinge eines Schustermessers. Zeigen Sie, sie ist ebenso groß wie die rechte Kreisfläche.
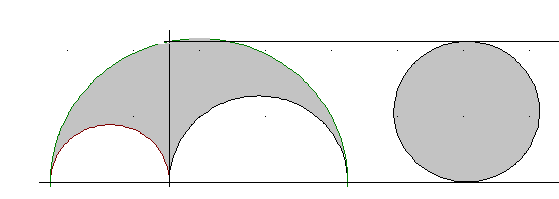
Mit den Größen p, q und h aus der Skizze gilt:
$$ \frac{π}{2}·\frac{(p+q)^2}{4} - \frac{π}{2}·\frac{p^2}{4} - \frac{π}{2}·\frac{q^2}{4} = \frac{π}{8}·\left[ (p+q)^2 - p^2 - q^2 \right] = \frac{π}{8}·2pq = π·\frac{h^2}{4} $$
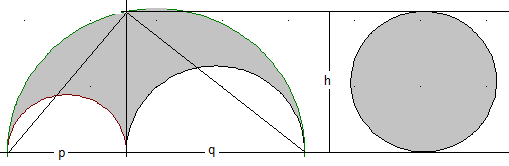
Satz von Tabit:
In einem stumpfwinkligem Dreieck ABC liege D auf \( \overline {AB} \), sodass die Dreiecke ABC und ADC ähnlich sind. Dann ist das Quadrat mit der Seite \( \left| {\overline {AC} } \right| \) flächengleich zum Rechteck aus \( \left| {\overline {AD} } \right| \) und \( \left| {\overline {AB} } \right| \).
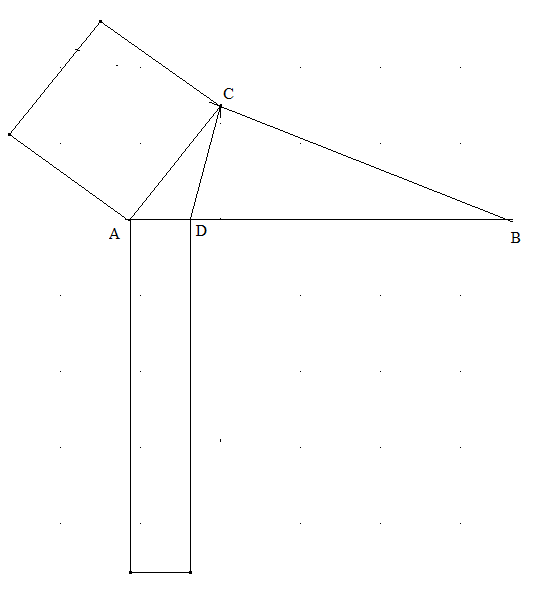
Beweisen Sie diesen Satz.
Nennen Sie \( \left| {\overline {AC} } \right| = a \), \( \left| {\overline {AD} } \right| = d \) und \( \left| {\overline {AB} } \right| = c \). Dann gilt wegen der Ähnlichkeit der Dreiecke \( \frac{d}{a} = \frac{a}{c} \) und nach Multiplikation mit dem Hauptnenner a²=d·c.
Wie erhält man daraus den Kathetensatz von Euklid?
Wählen Sie in einem rechtwinkligen Dreieck d als Projektion von a auf c. Dann ist das der Kathetensatz.
Wie kann die diese Skizze zum Beweis des Satzes des Pythagoras verwendet werden?
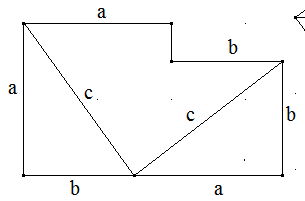
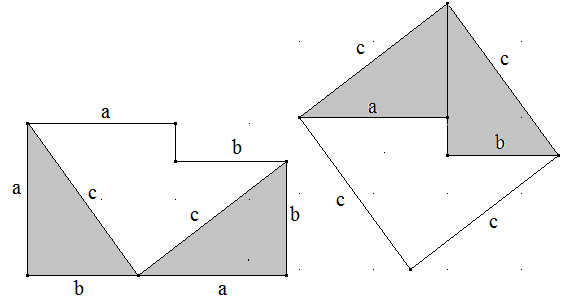
Die linke Figur (unten) hat den Flächeninhalt a²+b². Die rechte Figur hat den Flächeninhalt c². Verschieben Sie die grauen Dreiecke aus der linken Figur in die rechte Figur, dann ist a²+b²=c².
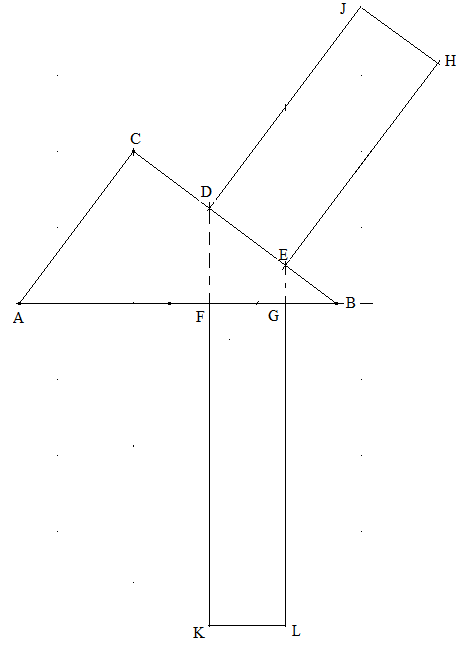
Kathetenwegsatz: Es sei ABC ein rechtwinkliges Dreieck und \( \overline {DE} \) ein beliebiger Abschnitt auf einer Kathete. F und G seien die Fußpunkte der Lote von D bzw. E auf AB. Über \( \overline {DE} \) hat das Rechteck DEHJ die Länge \( \left| {\overline {EH} } \right| = \left| {\overline {BC} } \right| \). Über \( \overline {FG} \) hat das Rechteck GFKL die Länge \( \left| {\overline {GL} } \right| = \left| {\overline {AB} } \right|. \)
Zeigen Sie, dass die Rechtecke DEHJ und GFKL flächengleich sind.
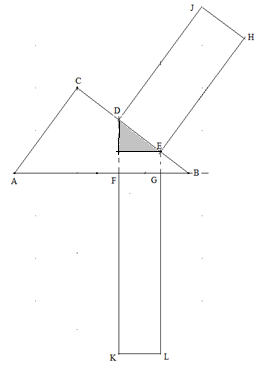
Das kleine graue Dreieck ist ähnlich zum Dreieck ABC. Daher gilt: Das Verhältnis der Hypotenusenlängen ist gleich dem Verhältnis der Längen der längeren Katheten:
\( \frac{ {\left| {\overline {DE} } \right|} }{ {\left| {\overline {AB} } \right|} } = \frac{ {\left| {\overline {FG} } \right|} }{ {\left| {\overline {BC} } \right|} } \) und daher \( |DE| · |BC| = |AB| · |FG| \) und wegen \( \left| {\overline {EH} } \right| = \left| {\overline {BC} } \right| \) und \( \left| {\overline {GL} } \right| = \left| {\overline {AB} } \right| \) gilt \( |DE|·|\overline{EH}| = |\overline{GL}|·|FG| \) .
Mit diesen Erkenntnissen lässt sich auch der Satz des Pythagoras beweisen. Führen Sie den Beweis.
Für \( \left| {DE} \right| = \left| {CB} \right| \) ist das der Kathetensatz und zusammen mit dem Kathetensatz zur anderen Kathete der Satz von Pythagoras.
