AB: Beweisen und Rechnen mit Kreisen (1)
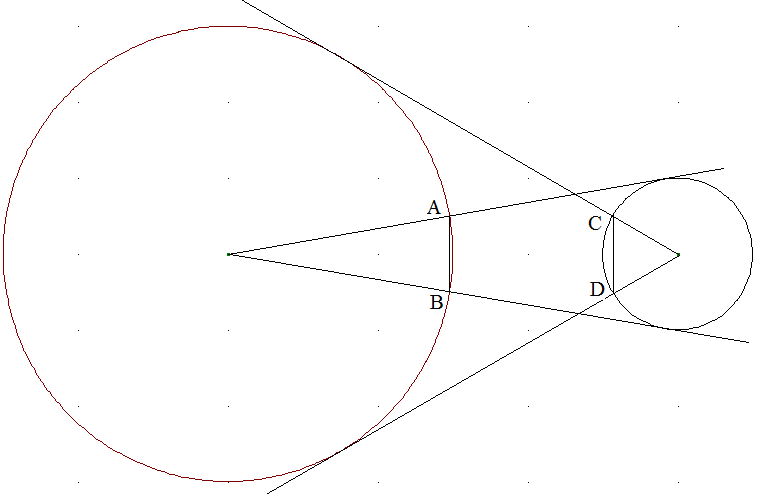
Gleichlange Sehnen: Gegeben sind ein großer und ein kleiner Kreis, die sich nicht berühren oder überschneiden. Vom Mittelpunkt des großen Kreises werden die Tangenten an den kleinen Kreis gelegt. Sie schneiden den großen Kreis in A und B. Vom Mittelpunkt des kleinen Kreises werden die Tangenten an den großen Kreis gelegt. Sie schneiden den kleinen Kreis in C und D.
Beweisen Sie: Die Sehnen \(\overline {AB} \) und \(\overline {CD} \) sind gleichlang.
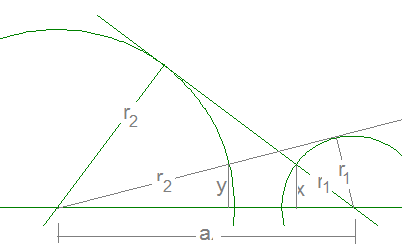
Sei a der Abstand der Mittelpunkte, r1 der Radius des kleinen Kreises und r2 der Radius des großen Kreises. x und y seien jeweils die halben Sehnen. Dann gelten wegen der Ähnlichkeit entsprechender Dreiecke \(\frac{x}{r_1} = \frac{r_2}{a} \) und \(\frac{y}{r_2} = \frac{r_1}{a}\) und daher \( x = y = \frac{r_1 · r_2}{a} \).
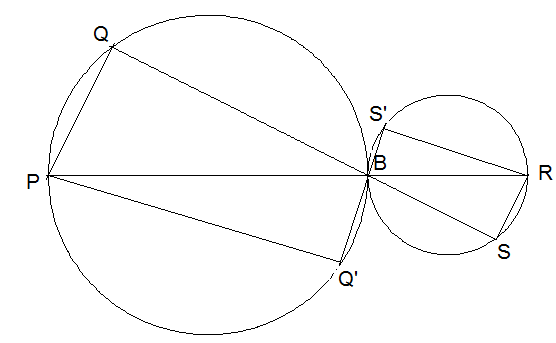
Art des Vierecks? Zwei Kreise K1 und K2 berühren sich in B. Eine Gerade g1 durch B schneidet K1 außer in B auch in P und K2 außer in B auch in R. Eine andere Gerade g2 durch B schneidet K1 in Q und K2 in S. Welcher Art Viereck ist PQRS?
Legen Sie PR zunächst durch die Mittelpunkte der beiden Kreise, Dann stimmen die Dreiecke PBQ und PSR in allen Winkelgrößen überein und sind folglich ähnlich. Die gleiche Argumentation begründet auch, dass PQ'B und BRS' ähnlich sind. Damit sind die Vierecke PQ'BQ und BSRS' ähnlich. Sie sind Bild und Urbild einer zentrischen Streckung mit den Zentrum B. Dann sind QQ' und S'S parallel und QQ'SS' ist ein Trapez. Nach Umbenennung von S' in R und von Q' in P folgt QPSR ist ein Trapez.
Inkreis und Umkreis von Vierecken
Ein Drachen der einen Umkreis hat, soll „Sehnendrachen" heißen. Welche Gemeinsamkeit haben alle Sehnendrachen?
Drachen mit zwei gegenüberliegenden rechten Winkeln sind Sehnendrachen.
Ein Trapez, das einen Inkreis hat soll „Tangententrapez" heißen. Welche Gemeinsamkeit haben alle Tangententrapeze?
Symmetrische Trapeze mit dem Schnittpunkt der Winkelhalbierenden auf der Symmetrieachse sind Tangententrapeze.
Gibt es einen Drachen und ein Trapez mit gemeinsamem Um- und Inkreis?
Konstruieren Sie ein Trapez mit dem Schnittpunkt der Winkelhalbierenden auf der Symmetrieachse einschließlich Um- und Inkreis. Der Umkreis schneidet die Symmetrieachse in R und S. Die Tangenten von R und S an den Inkreis bilden einen Drachen.
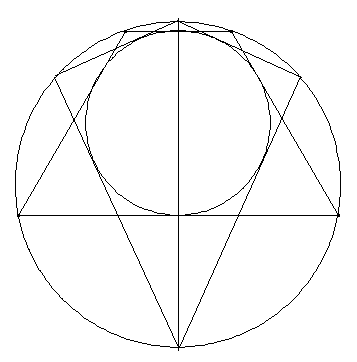
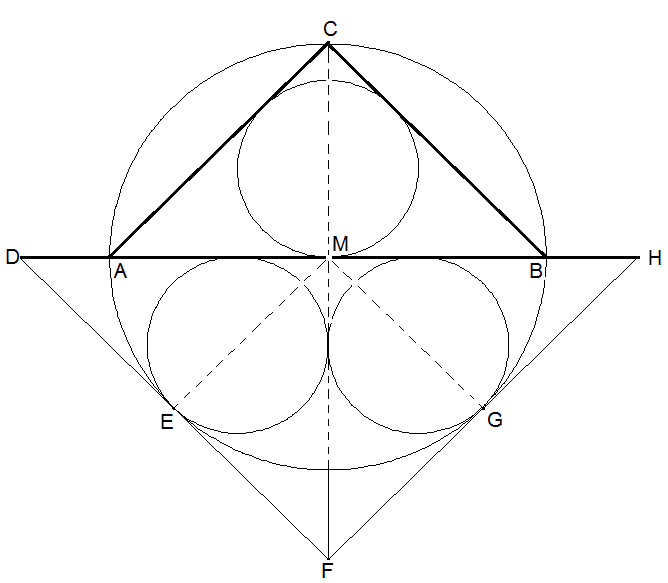
Kreise mit gleichen Radien: Ein Kreis K1 wird von seinem Durchmesser in zwei Halbkreise geteilt. In den einen Halbkreis wird ein gleichschenklig-rechtwinkliges Dreieck mit dem Durchmesser von K1 als Basis samt Inkreis K2 des Dreiecks gezeichnet. In den anderen Halbkreis werden zwei gleichgroße Kreise K3 und K4 gezeichnet, die sich untereinander und zusätzlich den Durchmesser und den Halbkreisbogen von K1 berühren (siehe Abbildung). Zeigen Sie, dass K2 und K3 den gleichen Radius haben.
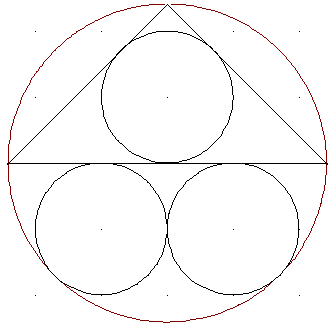
Wir ergänzen die in der Aufgabe gegebene Skizze um gemeinsame Tangenten DF bzw. FH an den kleinen und den großen Kreis. ann sind die gleichschenklig rechtwinkligen Dreiecke AMC, DEM, EFM, FGM und MBC kongruent, denn sie stimmen alle in ihren Kathetenlängen überein. Dann sind auch die daraus zusammengesetzten Dreiecke ABC, CFM und MFH kongruent. Kongruente Dreiecke haben gleichgroße Inkreise.