AB: Beweisen und Rechnen mit Kreisen (3)
Fünf Kreise: Gegeben sind 5 gleichgroße Kreise im Koordinatensystem. Alle berühren die x-Achse, zwei haben ihren Mittelpunkt auf der y-Achse (siehe Abbildung). Welche Steigung hat eine Gerade die die Gesamtfläche der 5 Kreise halbiert?
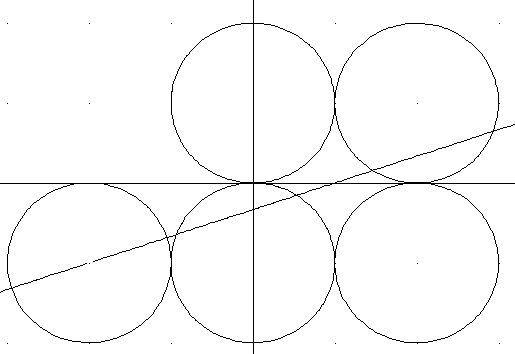
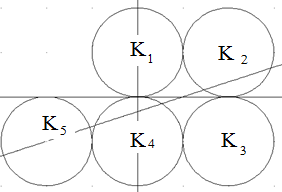
Der gemeinsame Radius aller Kreise sei r. Die Fläche der Kreise K1 bis K4 wird von jeder Geraden gm halbiert, die durch P(r|0) geht. Da gm auch K5 halbieren muss, muss gm durch den Mittelpunkt von K5 Q(-2r|-r) gehen. Die Gerade PQ hat den Differenzenquotienten \(\frac{0 + r}{r + 2r} = \frac{1}{3}\).
Halbierung eines gleichseitigen Dreiecks: Die Fläche des gleichseitigen Dreiecks KLM wird einerseits vom Bogen \(\widehat {CD}\) (auf Kreis um M) und andererseits von der zu KL parallelen Strecke \(\overline {AB} \) halbiert. Was ist länger \(\overline {AB} \) oder \(\widehat {CD}\)?
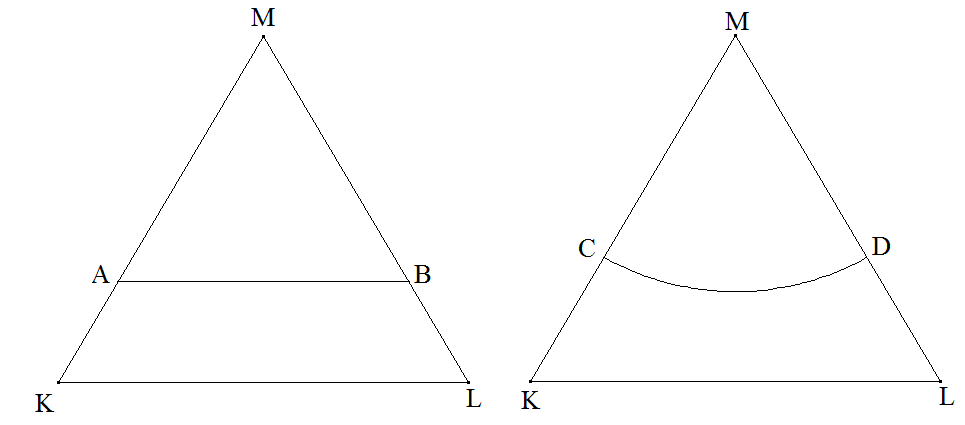
Das gleichseitige Dreieck KLM habe die Seitenlänge 2 und folglich die Höhe √3 (Satz des Pythagoras). Seine Fläche wird halbiert durch Stauchung mit dem Faktor \(\frac{1}{ {\sqrt{2} } }\). Dann gilt \(\left| {\overline {AB} } \right| = \frac{2}{ {\sqrt{2} } } \approx 1,4\). \({F_{KLM} } = \frac{ {2\sqrt{3} } }{2} = \sqrt{3} \). Welchen Radius r muss ein Sechstelkreis haben, damit seine Fläche \(\frac{ {\sqrt{3} } }{ {2\;} }\) ist? Ansatz \(\frac{ {\pi {r^2} } }{6} = \frac{ {\sqrt{3} } }{2}\) nach r aufgelöst \(r = \sqrt {\frac{3}{\pi }\sqrt{3} } \). Dann ist der Bogen \( \widehat {CD} = \frac{π}{3}·\sqrt{\frac{3}{π}·\sqrt{3}} ≈ 1,3 \).
Kleine Kreise im großen: Einem Kreis K mit dem Radius r werden zwei kleinere K1 mit dem Radius \(\frac{r}{2}\) einbeschrieben, die sich sowohl untereinander als auch K berühren. Dann werden dem Objekt aus drei Kreisen zwei Kreise K2 mit dem Radius x einbeschrieben, die beide Kreise K1 und auch K berühren. Und schließlich werden dem Objekt aus fünf Kreisen vier noch kleine K3 mit dem Radius z einbeschrieben, die K, K1 und K2 berühren. Welchen Anteil des Kreises K bedecken die vier Kreise K3?
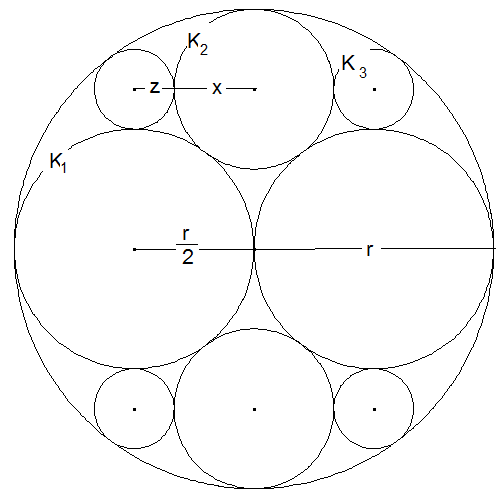
In der Skizze sieht man ein rechtwinkliges Dreieck, in dem gilt: \({\left( {\frac{r}{2} + x} \right)^2} = {\left( {r - x} \right)^2} + {\left( {\frac{r}{2} } \right)^2}\). Nach einiger Umformung erhält man daraus (1) r = 3x. Außerdem sieht man, dass der kleinste Abstand der Mittelpunkte von K1 und K3 gleich \( \frac{r}{2} + z = r - x\; \)ist. Zusammen mit (1) erhält man daraus r = 6z. Nun ist \( 4πz^2 = 4π·\left( \frac{r}{6} \right)^2 = \frac{πr^2}{9} \), also \(\frac{1}{9}\) der Fläche von K.
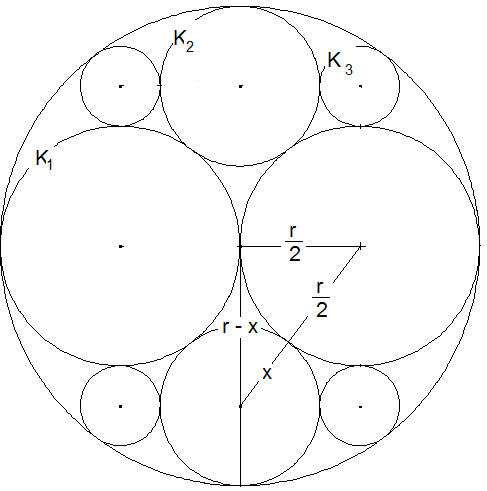
Inkreis, Ankreis, Umkreis: Ein Kreis K1 wird von seinem Durchmesser in zwei Halbkreise geteilt. In den einen Halbkreis wird ein gleichschenklig-rechtwinkliges Dreieck mit dem Durchmesser von K1 als Basis samt Inkreis K2 des Dreiecks gezeichnet. In den anderen Halbkreis werden zwei gleichgroße Kreise K3 und K4 gezeichnet, die sich untereinander und zusätzlich den Durchmesser und den Halbkreisbogen von K1 berühren (siehe Abbildung). Zeigen Sie, dass K2 und K3 den gleichen Radius haben.
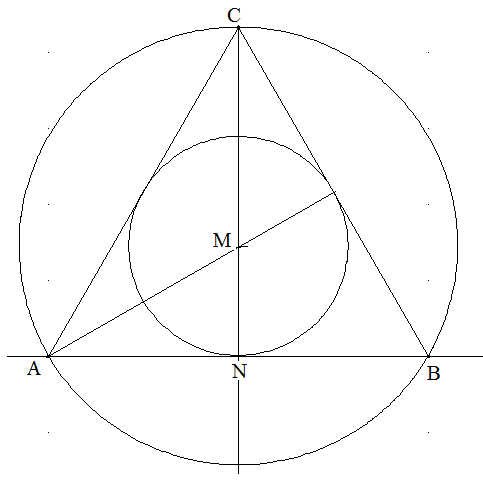
Konstruieren Sie ein gleichseitiges Dreiecke mit seinen sogenannten Ankreisen.
Spiegeln Sie das gleichseitige Dreieck an jeder Seite. Dann erhalten Sie als Bildpunkte, die nicht auf den Spiegelachsen liegen, die Ankreismittelpunkte.
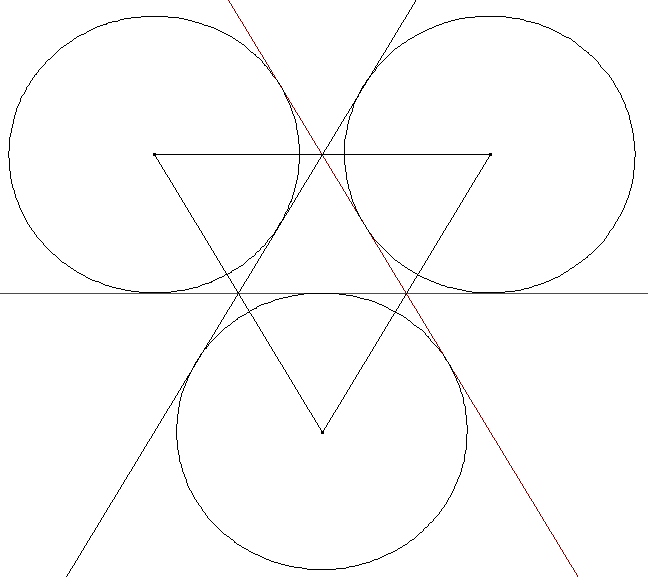
Begründen Sie, dass die Radien von Inkreis, Umkreis und Ankreis eines gleichseitigen Dreiecks das Längenverhältnis 1:2:3 haben.
In einem gleichseitigen Dreieck sind Mittelsenkrechte, Winkelhalbierende und Seitenhalbierende identisch. Daher ist der Mittelpunkt der M des Umkreises auch der Mittelpunkt des Inkreises und auch der Schnittpunkt der Seitenhalbierenden. Letztere werden durch ihren Schnittpunkt M im Verhältnis 2:1 geteilt. \({r_2} = \left| {\overline {CM\;} } \right|\) ist der Radius des Umkreises. N sei die Seitenmitte von \(\overline {AB} \). Dann ist \(\left| {\overline {MN} } \right|\) der Radius r1 des Inkreises. Folglich gilt r1 : r2 = 1:2. P sei der Fußpunkt des Lotes von einem Mittelpunkt eines Ankreises auf die berührende Dreiecksseite. Dann \(\left| {\overline {FP} } \right| = {r_1} + {r_2} = {r_3}\) und folglich r1:r2:r3= 1:2:3.