AB: Beweisen und Rechnen mit Kreisen (6)
Ein besonderer Punkt im Dreieck: Auguste Miquel (um 1816 – 1851) hat 1838 folgenden Satz veröffentlicht: Ist A′ irgendein Punkt auf der Seite BC eines Dreiecks, entsprechend B′ auf AC und C′ auf AB, so schneiden sich die Kreise durch A, B′ und C′, durch A′, B und C′ sowie durch A′, B′ und C in genau einem Punkt.
Beweisen Sie diesen Satz mit Hilfe des Satzes: Ein Viereck ist genau dann Sehnenviereck, wenn die Größen gegenüberliegender Winkel die Summe 180° haben.
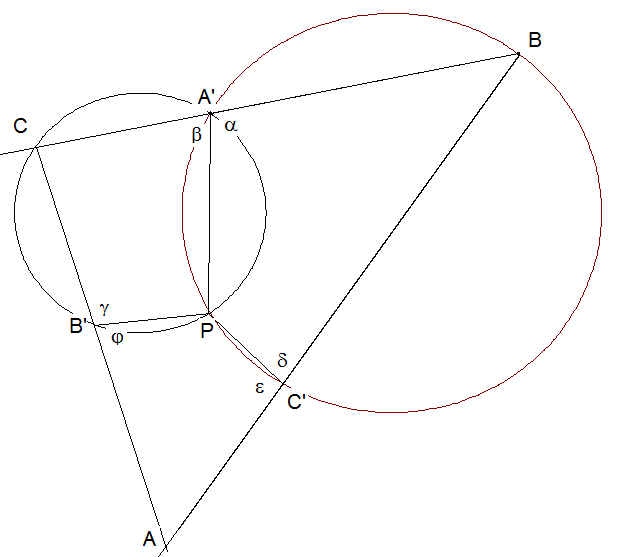
Zeichnen Sie das Dreieck ABC mit den Punkten A', B' und C' auf den Seiten. Konstruieren Sie dann den Kreis K1 durch A', B und C' sowie den Kreis K2 durch B', A' und C. Die Kreise schneiden sich außer in A' in P. Zeichnen Sie die Strecken PA'. PB' und PC'. Dabei entstehen die Winkel α, β, γ, δ, ε und ϕ. γ ergänzt sich sowohl mit β als auch mit ϕ zu 180°. Daher ist β=ϕ. Aus entsprechenden Gründen sind ε=α. Aus β+α=180° folgt, dass auch ϕ und ε sich zu 180° ergänzen und somit AC'PB' ein Sehnenviereck ist. Damit liegen auch die Punkte A , C' und B' auf einem Kreis.
Raute im Sehnenviereck: Das Bild zeigt ein Sehnenviereck mit den Winkelhalbierenden seiner verlängerten Seiten.
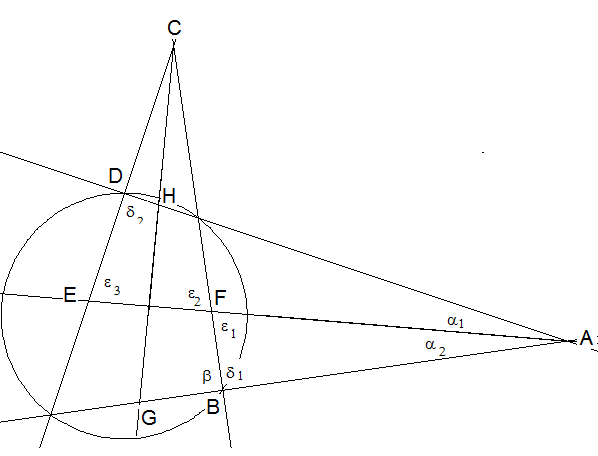
Zeigen Sie: Die Dreiecke EAD und BAF sind ähnlich.
In der Abbildung haben gleichgroße Winkel abgesehen von der Fußnote gleiche Bezeichnungen.
α1 = α2 (Winkelhalbierende), ε1 = ε2 (Scheitelwinkel), δ1 = δ2 (ergänzen β zu 180°. Daher stimmen die Dreiecke EAD und BAF in zwei Winkeln überein und sind ähnlich.
Zeigen Sie: Das Dreieck EFC ist gleichschenklig.
ε2=ε3 (entsprechende Winkel in ähnlichen Dreiecken). Dreiecke mit gleichen Basiswinkeln sind gleichschenklig.
Begründen Sie: Das Dreieck GAH ist gleichschenklig.
Für das Dreieck HGA gilt das Gleiche, wie für das Dreieck EFC da die Problemstellung bis auf Drehung und Verzerrung identisch ist.
Begründen Sie: HEGF ist eine Raute.
In gleichschenkligen Dreiecken sind Halbierende des Gegenwinkels der Basis gleichzeitig Mittelsenkrechte der Basis. Daher halbieren sich EF und HG mit ihrem Schnittpunkt und stehen senkrecht aufeinander. Vierecke mit zueinander senkrechten, sich halbierenden Diagonalen sind Rauten.
