AB: Beweisen und Rechnen mit Kreisen (7)
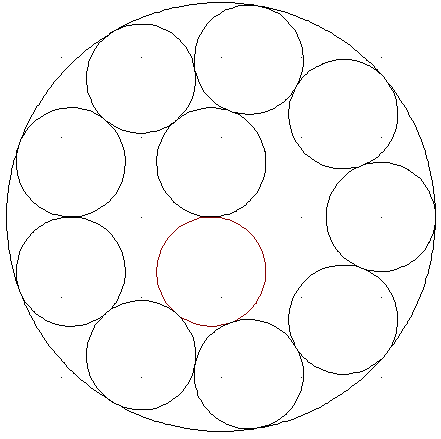
Elf Kreise im Kreis
Welchen Radius ein Kreis, in dem 11 Einheitskreise in der dargestellten Weise Platz finden.
xxx
Neunzehn Kreise in einem Kreis:
Beide Kreise enthalten je 19 kleinere Kreise der gleichen Größe, deren Mittelpunkte einmal auf konzentrischen Kreisen und einmal auf regelmäßigen Sechseckenliegen. Wieviel % der größeren Kreisfläche beträgt die kleinere Kreisfläche?
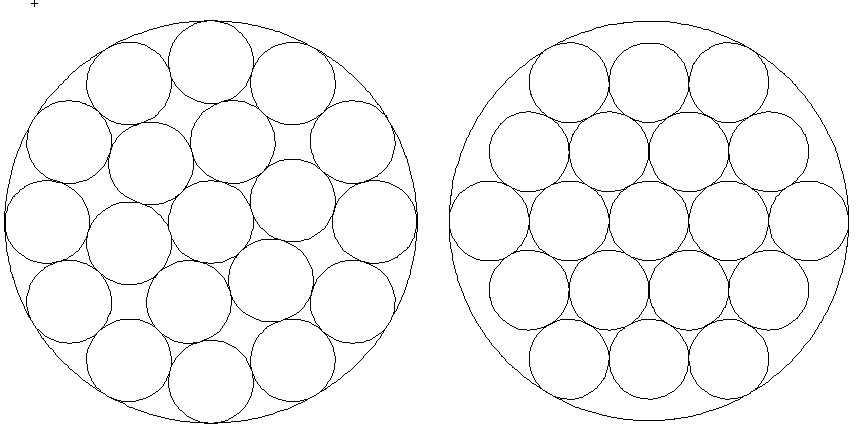
Auch 37 Kreise lassen sich so anordnen, dass ihre Mittelpunkte einmal auf konzentrischen Kreisen und einmal auf regelmäßigen Sechseckenliegen. Wieviel % der größeren Kreisfläche beträgt dann die kleinere Kreisfläche?
Dosen in einer Kiste mit quadratischer Grundfläche:
25 Dosen mit jeweils dem Radius r können in einer Kiste mit quadratischer Grundfläche der Größe 100r² untergebracht werden. Wieviel % der Grundfläche können maximal eingespart werden, wenn man 24 Dosen mit dem Radius r in einer quadratischen Kiste wie dargestellt anordnet?
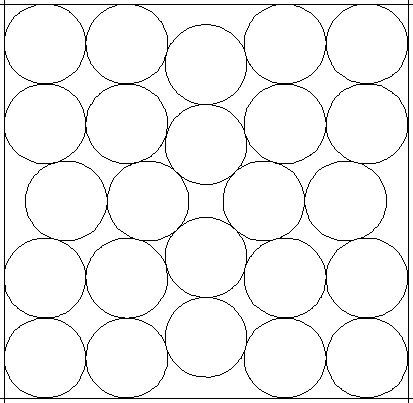
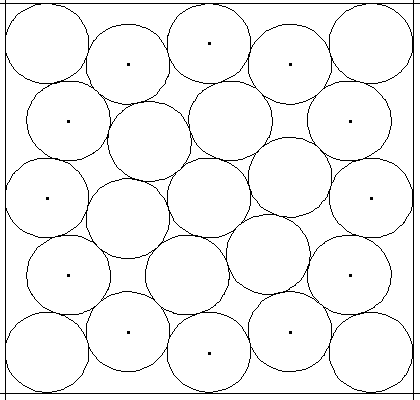
Man kann auch 23 Dosen in eine quadratische Kiste packen. Wieviel % Grundfläche spart man jetzt gegenüber einer Kiste mit 25 Dosen?
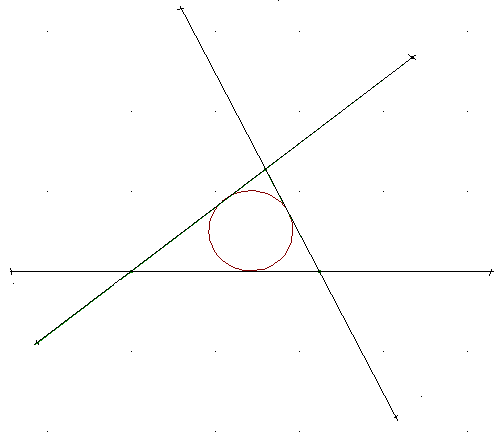
Der Conway-Kreis: Die Seiten eines Dreiecks werden über jeden Eckpunkt hinaus so ver-längert, wie die Länge der dem Eckpunkt gegen-über-liegende Seite angibt. John Horton Conway hat entdeckt, dass die Endpunkte dieser Verlängerungen auf einem Kreis liegen. Beweisen Sie dies. Hinweis: Die Berührpunkte des Inkreises teilen jede Dreiecksseite in zwei Abschnitte, sodass man für den Beweis mit drei Längen-bezeichnungen auskommt.
xxx
Kreis im Schustermesser
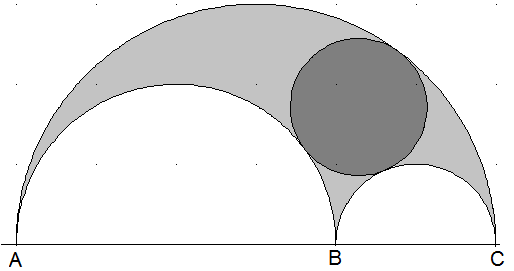
AC sei der Durchmesser eines Halbkreises K1 mit dem Radius 3. B liege auf AC. AB sei der Durchmesser eines Halbkreises K2 mit dem Radius 2. BC sei der Durchmesser eines Halbkreises K3 mit dem Radius 1. Scheidet man aus K1 die Halbkreise K2 und K3 heraus bleibt eine Form stehen, die man als Schustermesser bezeichnet. Welchen Radius hat der größte Kreis (dunkelgrau), den man aus einem Schustermesser heraus schneiden kann?
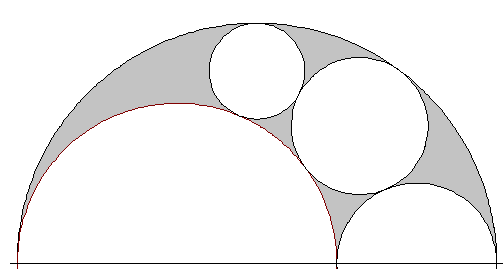
Nachdem ein größter Kreis aus den Schustermesser herausgeschnitten wurde, soll aus dem größten verbliebenen Teil der Klinge ein größter zweiter Kreis herausgeschnitten werden (siehe Abbildung). Welchen Radius hat dieser?
Längenverhältnis aus Radius und Tangente
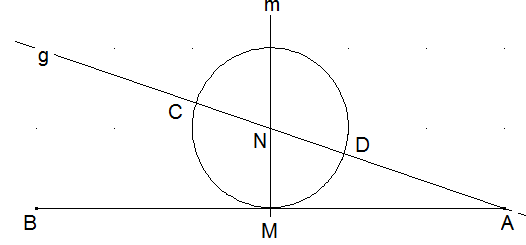
Der Mittelpunkt der Strecke AB sei M und m sei die Mittelsenkrechte auf AB. Eine Gerade g durch A schneide m in N. Der Kreis um N mit dem Radius \( | \overline { M N } | \) schneide g in C und D (siehe Abbildung). Welches Längenverhältnis \( = \frac { \overline { M N } } { \overline { M A } } \) entsteht im Falle \( | \overline { C D } | = | \overline { D A } | \)?
xxx
