AB: Besondere Geometrie-Aufgaben (2)
Geometrische Reihe: Gegeben sei ein Rechteck ABCD mit der Seitenlänge \(\left| {\overline {AD} } \right| = 1\). Das Rechteck ist so gewählt, dass darin das Einheitsquadrat AEGD und das zu ABCD ähnliche Rechteck PFCG sowie ein Rechteck EBFP Platz finden. Dann liegt P auf der Diagonalen AC (Strahlensatz; siehe Abbildung).
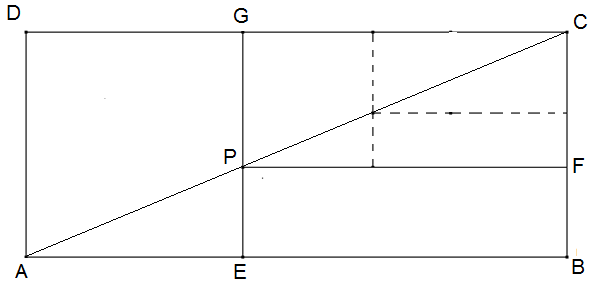
Das Rechteck PFCG ist das Bild von ABCD bei zentrischer Streckung (besser: Stauchung) mit dem Streckzentrum C und dem Streckfaktor q < 1. Drücken Sie die Seitenlängen und den Flächeninhalt des Rechtecks EBFP mit Hilfe von q aus.
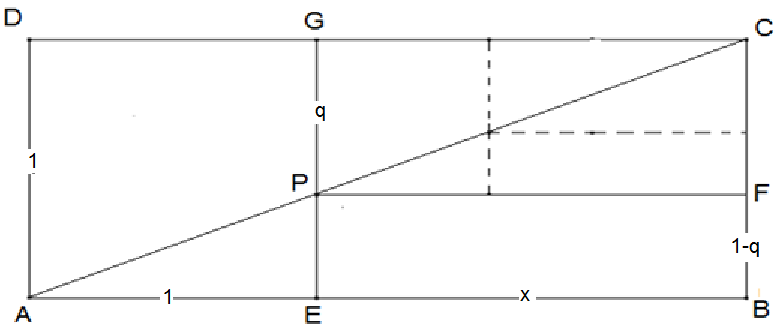
Es sei x = \(\left| {\overline {EB} } \right| = \left| {\overline {PF} } \right| = \left| {\overline {GC} } \right|\) Nach dem zweiten Strahlensatz gilt: \(\frac{x}{q} = \frac{ {x + 1} }{1}\) und daher \(x = \frac{q}{ {1 - q} }\). Weil \(\left| {\overline {FB} } \right| = 1 - q\), hat das Rechteck EBFP den Flächeninhalt q.
Die genannte zentrische Streckung soll auch \(\left| {\overline {EG} } \right|\) und \(\left| {\overline {PF} } \right|\) abbilden (Bilder gestrichelt angedeutet). Welchen Flächeninhalt haben die Bilder von AEGD und EBFP?
Bei zentrischer Stauchung mit dem Faktor q werden Flächen mit dem Faktor q² gestaucht. Daher hat das Bild von AEGD den Flächeninhalt q² und das Bild von EBFP den Flächeninhalt q³.
Drücken Sie die Fläche des Rechtecks ABCD durch q aus und nennen Sie eine Formel für die Summe \({q^0} + {q^1} + {q^2} + {q^3},\; \ldots \) mit unendlich vielen Summanden.
In Rechteck ABCD finden ein Quadrat der Fläche 1=q0, ein Rechteck der Fläche q und eine rechteckige Restfläche PFCG Platz. In der Restfläche finden ein Quadrat der Fläche q2, ein Rechteck der Fläche q³ und eine rechteckige Restfläche zweiter Ordnung Platz. In der Restfläche zweiter Ordnung finden ein Quadrat der Fläche q4, ein Rechteck der Fläche q5 und eine rechteckige Restfläche dritter Ordnung Platz. Und so weiter. Im Rechteck ABCD finden insgesamt Flächen der Größen q0, q1, q2, q3, q4, q5, …. Platz. Andererseits ist FABCD=1+\(\frac{q}{ {1 - q} } = \frac{1}{ {1 - q} }\). Also gilt \(\frac{1}{ {1 - q} } = \) q0, q1, q2, q3, q4, q5, …
Das Fibonacci-Prinzip: Bilden Sie eine Zahlenfolge auf folgende Weise: Legen Sie die ersten beiden Glieder der Folge beliebig fest. Ein nächstes Folgenglied ist immer die Summe der beiden Vorgänger. Beispiel: Die ersten beiden Folgenglieder seien 2 und 5 (frei festgelegt). Dann ist das dritte Folgenglied 7 (= 2 + 5) und es geht so weiter 2, 5, 7, 12, 19, 31, … Das 7. Folgenglied ist 50. Zeigen Sie: Die Summe der ersten 10 Folgenglieder ist (unabhängig von den Startgliedern) das 11-fache des siebten.
Die ersten beiden Glieder seien a und b. Dann wird die Folge durch diese Wertetabelle wiedergegeben:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| a | b | a+b | a+2b | 2a+3b | 3a+5b | 5a+8b | 8a+13b | 13a+21b |
Das 10. Glied ist 21a+34b. Die Summe der ersten 10 Glieder ist 55a+88b. Das 11-Fache des 7. Gliedes ist 55a+88b.
Kongruente Dreiecke: Gegeben sei ein beliebiges Dreieck GHE. EHCB sei das Quadrat über EH. FGED sei das Quadrat über GE und JKHG sei das Quadrat über GH. DEBA und KICH seien Parallelogramme.
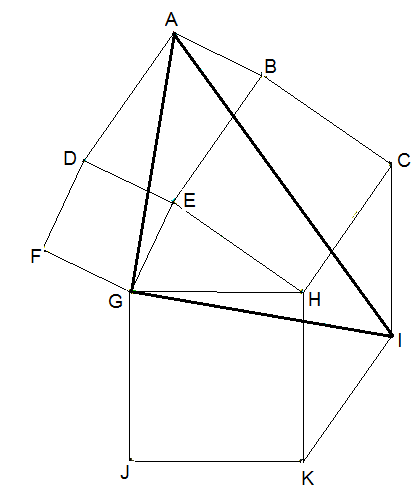
Zeigen Sie die Kongruenz der Dreiecke AEB, GHE und HIC.
Die Dreiecke AEB und GHE stimmen in den Längen zweier Seiten überein. Die Seiten \(\left| {\overline {BE} } \right|\) und \(\left| {\overline {EH} } \right|\) grenzen an das gleiche Quadrat und \(\left| {\overline {AB} } \right| = \left| {\overline {DE} } \right|\) (Parallelogramm) sowie \(\left| {\overline {GE} } \right| = \left| {\overline {DE} } \right|\) (Quadrat). β und α2 ergänzen sich zu 180° (Vollwinkel - 2·90°). Auch β und α1 ergänzen sich zu 180° (Parallelogramm). Daher ist α1=α2, und die Dreiecke sind kongruent. Ein entsprechender Beweis lässt sich zu Kongruenz der Dreiecke GHE und HIC führen.
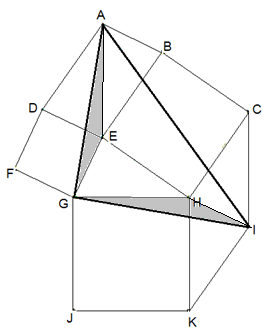
Zeigen Sie: AGI ist gleichschenklig.
Die Vollwinkel um H und um E sind aus je 5 Winkeln zusammengesetzt, wovon 4 paarweise gleichgroß sind. Also gilt das auch für den fünften. Die Dreiecke GEA und GIH stimmen in zwei Winkeln und zwei Seiten überein. Deshalb ist \(\left| {\overline {AG} } \right| = \left| {\overline {GI} } \right|\), und das Dreieck AGI ist gleichschenklig.
Langleys Aufgabe: Der britische Mathematiker E.M. Langley gründete 1884 „The Mathematical Gazette". Darin wurde (sinngemäß) folgende Aufgabe abgedruckt:
Im Dreieck ABC sind vier Winkelgrößen gegeben (siehe Abbildung) und \(\overline {AD} \) ist Hilfslinie mit der Länge \(\left| {\overline {AB} } \right|\).
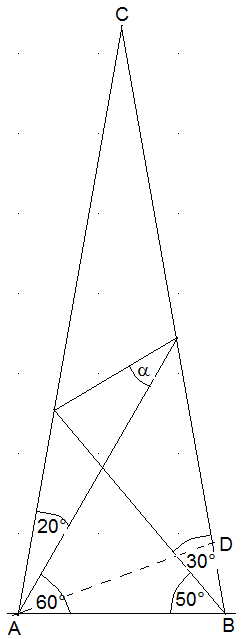
Tragen Sie alle Winkelgrößen, die sich aus den gegebenen schließen lassen, in die Skizze ein.
| Nr | Größe | Begründung |
| 1 | 20° | Winkelsumme ABC |
| 2 | 20° | ABC ähnlich zu ABD |
| 3 | 70° | Winkelsumme ABE |
| 4 | 70° | Scheitelwinkel |
| 5 | 110° | Nebenwinkel |
| 6 | 50° | Winkelsumme AEF |
| 7 | 40° | Winkelsumme ABG |
Wo liegen gleichschenklige Dreiecke? Umgrenzen Sie diese (ggf. durch eine weitere Hilfslinie).
Eine weitere Hilfslinie ist FD. Jetzt ist ABF gleichschenklig (gleiche Basiswinkel) und ADF gleichseitig (gleichschenklig mit einem 60°-Winkel). Dann ist FDG gleichschenklig (gleiche Basiswinkel). Es gilt \(\left| {\overline {AD} } \right| = \left| {\overline {GD} } \right|\) (gleiche Basiswinkel im Dreieck ADG), und es gilt \(\left| {\overline {AD} } \right| = \left| {\overline {FD} } \right|\) (gleichseitiges Dreieck ADF). Dann ist das Dreieck FDG gleichschenklig und daher (1) δ=α+40°.
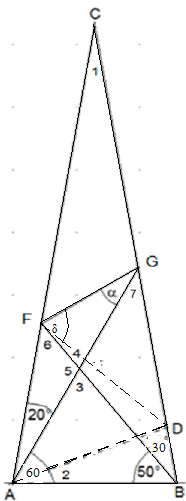
Bestimmen Sie die Größe des Winkels α.
Außerdem ist δ+10°+30°+40°+α=180° und folglich (2) δ+α=100°. Aus (1) und (2) folgt α=30°.
