AB: Besondere Geometrie-Aufgaben (4)
Bewegungsaufgabe und harmonisches Mittel: Das Trapez ABCD hat bei A und bei B je einen rechten Innenwinkel (siehe Abbildung).
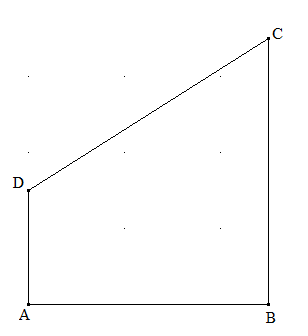
Es sei \(\left| {\overline {BC} } \right| = a\) und \(\left| {\overline {AD} } \right| = b\). Welchen Abstand hat der Diagonalenschnittpunkt des Trapezes ABCD von der Strecke AB?
Aus dem letzten AB (Aufgabe 3) wissen wir: Der gesuchte Abstand ist das halbe harmonische Mittel aus a und c, nämlich \( \frac{ab}{a + b} \).
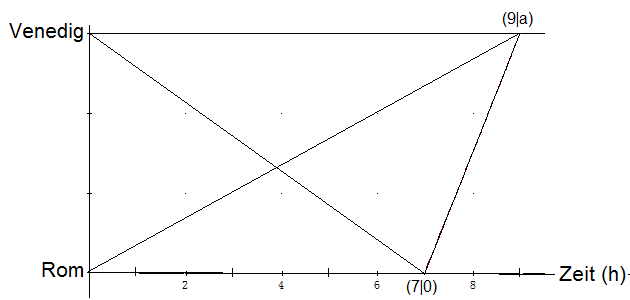
Der Papst sendet einen Boten mit einer Nachricht von Rom nach Venedig, der sich Tag und Nacht in gleichmäßigem Tempo fortbewegt und für die gesamte Strecke 9 Tage braucht. Der Empfänger der Nachricht eilt dem päpstlichen Boten Tag und Nacht in gleichmäßigem Tempo entgegen und hätte für die ganze Strecke 7 Tage gebraucht. Wann begegnen sich die beiden, wenn sie gleichzeitig starten.
Stellen Sie die Gegebenheiten in einem Weg-Zeit-Diagramm dar. Die Entfernung Rom-Venedig sei a. Dann ist die t-Koordinate des Schnittpunktes der Geraden mit den Gleichungen \(y = \frac{ {ax} }{9}\) und \(y = \frac{ {a\left( {x - 7} \right)} }{ { - 7} }\) die Lösung. Leichter ist es aber, sich auf ein Ergebnis aus dem letzten AB (Aufgabe 3) zu beziehen und das halbe harmonische Mittel von 9 und 7 zu berechnen. In jedem Falle treffen sich die beiden 1,5 Stunden vor Ablauf des vierten Tages nach Start.
Der Satz von Ceva: Der italienische Mathematiker Giovanni Ceva (1647 bis 1734) bewies 1678 in seinem Werk „De lineis rectis" den Satz:
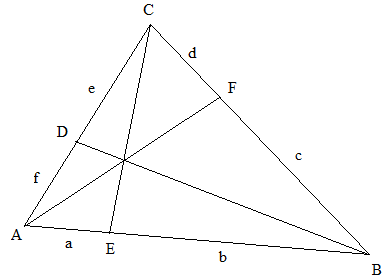
Wenn auf den Seiten eines Dreiecks ABC die Punkte D, E und F liegen, welche die Seiten in den Verhältnissen \(\frac{a}{b}\), \(\frac{c}{d}\) und \(\frac{e}{f}\) teilen und die Strecken von je einem Eckpunkt des Dreiecks zum gegenüberliegenden Teilungspunkt durch einen gemeinsamen Punkt gehen, dann ist das Produkt der Teilungsverhältnisse gleich 1 (\( \frac{f}{e}·\frac{b}{a}·\frac{d}{c} = 1 \)).
Zum Beweis braucht man den folgenden Hilfssatz:
Im Dreieck ABC teilt D die Strecke \(\overline {AB} \) im Verhältnis \(\frac{a}{b}\). E sei ein Punkt auf \(\overline {CD} \). Dann wird die Fläche des Dreiecks ABE von \(\overline {ED} \) im Verhältnis \(\frac{a}{b}\) geteilt. Auch die Flächen der Dreiecke AEC und EBC stehen in diesem Flächenverhältnis.
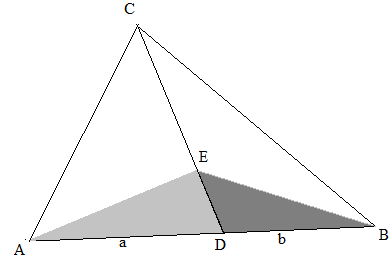
Beweisen Sie diesen Hilfssatz.
Mit den Bezeichnungen nebenstehender Skizze gilt: \( F_{ADE} = a·\frac{h}{2} \) und \( F_{DBE} = b·\frac{h}{2} \). Für Dreiecke gleicher Höhe gibt das Längenverhältnis der Grundseiten das Flächenverhältnis an.
\( F_{ADC} = a·\frac{H}{2} \)
\( F_{AEC} = F_{ADC} - F_{ADE} = a·\frac{H}{2} - a·\frac{h}{2} = a·\frac{H-h}{2} \) und
\( F_{EBC} = F_{DBC} - F_{DBE} = b·\frac{H}{2} - b·\frac{h}{2} = b·\frac{H-h}{2} \). Also gilt: \( \frac{F_{AEC}}{F_{EBC}} = \frac{a}{b} \)
Begründen Sie mit Hilfe der Skizze und dem Hilfssatz den Satz von Ceva.
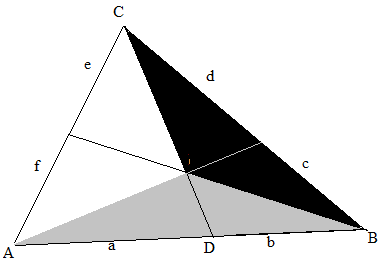
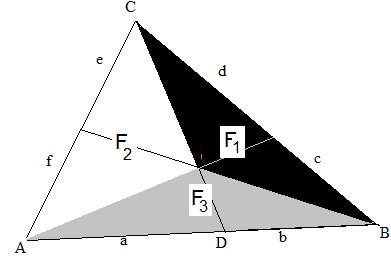
\(\frac{ { {F_1} } }{ { {F_2} } } = \frac{b}{a}\); \(\frac{ { {F_2} } }{ { {F_3} } } = \frac{d}{c}\); \(\frac{ { {F_3} } }{ { {F_1} } } = \frac{f}{e}\) (gemäß Hilfssatz).
\( \frac{b}{a} · \frac{d}{c} · \frac{f}{e} = \frac{F_1}{F_2} · \frac{F_2}{F_3} · \frac{F_3}{F_1} = 1 \)
Sätze über Winkel: Gegeben ist ein Dreieck ABC sowie sein Um- und Inkreis mit den Mittelpunkten M bzw. N. Die Gerade CM schneidet den Umkreis in D. Der Fußpunkt der Höhe durch C auf AB sei H.
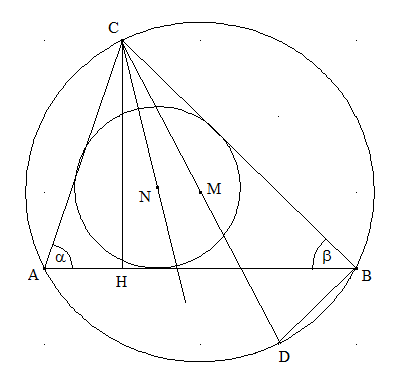
Beweisen Sie: Die Dreiecke AHC und DBC sind ähnlich.
Die hellgrauen Winkel sind gleichgroß (Umfangswinkel über dem gleichen Bogen CB). Die dunkelgrauen Winkel sind rechte Winkel (Winkel im Thaleskreis bzw. Winkel zwischen Höhe und Grundseite). Die Dreiecke AHC und DBC stimmen in zwei Winkelgrößen überein und sind folglich ähnlich.
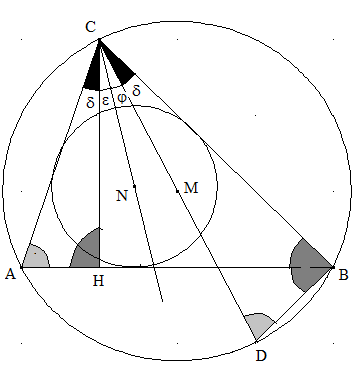
Beweisen Sie: Die Winkelhalbierende durch C im Dreieck ABC halbiert auch den Winkel HCM (das ist der Winkel zwischen HC und CM).
Die schwarzen Winkel sind gleichgroß (entsprechende Winkel in ähnlichen Dreiecken). Es gilt δ+ε=ϕ+δ (CN ist Winkelhalbierende). Nach Subtraktion von δ auf beiden Seiten gilt ε=ϕ. D.h. CN halbiert auch den Winkel HCM.
