AB: Satz des Pythagoras und verwandte Sätze (5)
Rechteck und Pythagoras: Einem rechtwinkligen Dreieck wird ein Rechteck so einbeschrieben, dass dessen Seite x auf der Kathete a, dessen Seite y auf der Kathete b, ein Eckpunkt auf der Hypotenuse c und dessen Diagonale d senkrecht auf der Hypotenuse c steht (siehe Abbildung). Zeigen Sie: ay+bx=cd und \( \frac{y}{a} = \frac{d}{c} = \frac{x}{b} \) und beweisen Sie mit Hilfe dessen den Satz des Pythagoras.
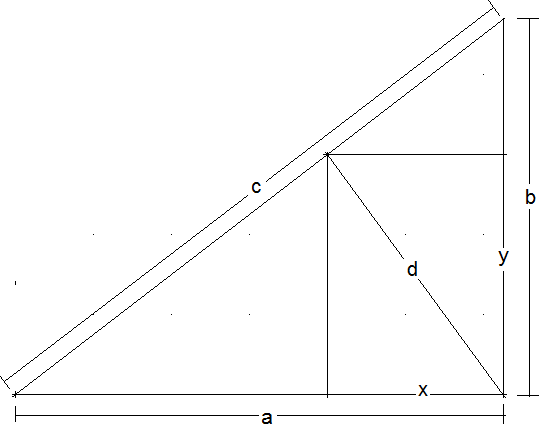
d zerlegt das Dreieck mit der Fläche ½·d·c in zwei Teildreiecke mit den Flächen ½·a·y und ½·b·x. Daher ist ½·d·c = ½·a·y + ½·b·x oder (1) d·c = a·y + b·x.
Alle rechtwinkligen Dreiecke in der Skizze sind ähnlich zueinander. Daher gilt \( \frac{ \text{Höhe} }{ \text{Hypotenuse} } = \frac{d}{c} = \frac{y}{a} = \frac{x}{b} \).
Daraus folgt (2) \( \frac{d·b}{c} = x \) und (3) \( \frac{d·a}{c} \).
(2) und (3) in (1) eingesetzt, ergibt \( d·c = \frac{a^2·d}{c} + \frac{b^2·d}{c} \). Durchmultiplizieren mit \( \frac{c}{d} \) ergibt a² + b² = c².
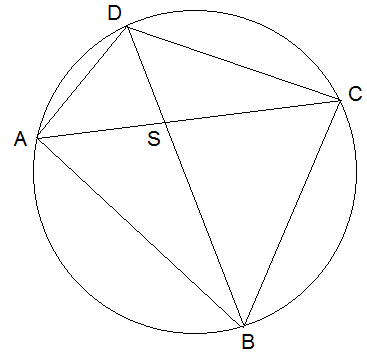
Sehnensatz und Höhensatz von Euklid: Der Sehnensatz lautet: Zwei Sehnen AC und BD eines Kreises schneiden sich in S. Dann gilt .
Zeigen Sie: Wenn eine Sehne Durchmesser des Kreises ist und die andere Sehne senkrecht dazu verläuft, dann ist der Sehnensatz identisch mit dem Höhensatz von Euklid.
Wählen Sie eine Sehne als Durchmesser ihres Kreises und eine Sehne senkrecht dazu. Dann ist der Sehnensatz gerade der Höhensatz von Euklid.
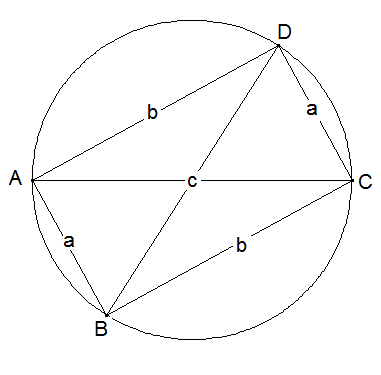
Ptolemäus und Pythagoras: Der Satz des Ptolemäus lautet: In einem Sehnenviereck ist das Produkt der Längen der Diagonalen gleich der Summe der Produkte der Längen gegenüberliegender Seiten. In einem Sehnenviereck ABCD gilt also. Beweisen Sie den Satz des Pythagoras mit Hilfe des Satzes von Ptolemäus.
Wählen Sie ein Rechteck als Sehnenviereck. Dann ist der Satz von Ptolemäus gerade der Satz von Pythagoras.
Pythagoreisches Dreieck aus zwei pythagoreischen Dreiecken: Ein rechtwinkliges Dreieck soll pythagoreisch heißen, wenn alle Seitenlängen natürliche Zahlen sind.
Zeigen Sie: Wenn das Tripel (a, b, c) aus den beiden Kathetenlängen a und b sowie der Hypotenusenlänge c ein pythagoreisches Tripel ist, dann sind auch (a²,ab,ac) sowie (ab,b²,bc) pythagoreische Tripel mit den Hypotenusenlängen ac bzw. bc.
Sei (a, b, c) ein pythagoreisches Tripel, dann gilt a²+b²=c² und nach Multiplikation mit a² gilt a²a²+a²b²=a²c² oder (a²)²+(ab)²=(ac)². Damit ist (a², ab, ac) ein pythagoreisches Tripel. Entsprechendes gilt für eine Multiplikation mit b².
Ein rechtwinkliges Dreieck wird entlang seiner Höhe h auf der Hypotenuse in zwei kleinere rechtwinklige Dreiecke zerlegt. Gibt es nun pythagoreische Dreiecke, die sich auf diese Weise in zwei pythagoreische Dreiecke aufteilen lassen?
Wählen Sie h = ab als Höhe eines rechtwinkligen Dreiecks mit den Katheten ac und bc sowie der Hypotenuse a²+b².
