AB: Regelmäßige n-Ecke und n,k-Sterne (1)
Einführung Regelmäßige n-Ecke und n,k-Sterne:
Ein regelmäßiges n-Eck ist ein geschlossener konvexer Streckenzug aus n gleichlangen Strecken mit n gleichgroßen Innenwinkeln.
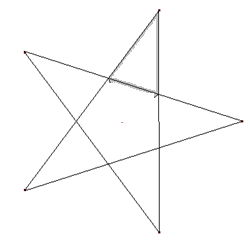
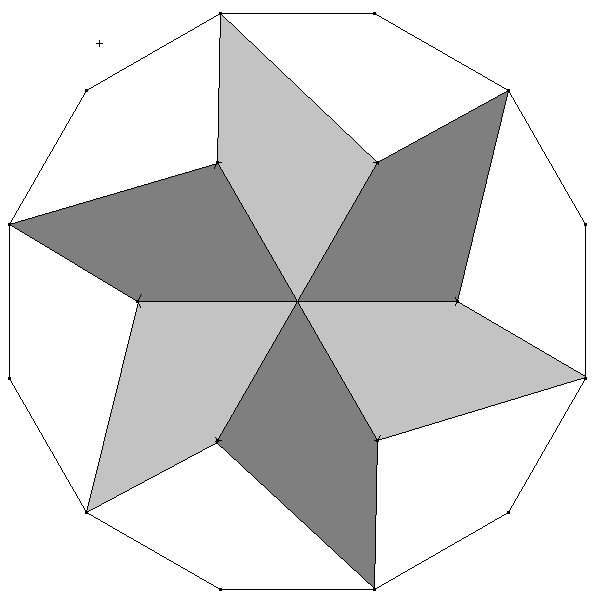
Ein n,k-Stern entsteht, wenn man n Punkte regelmäßig auf einem Kreis verteilt und die Punkte von A0 bis An-1 im Kreise herum benennt. Dann ergeben alle Verbindungsstrecken \(\overline { {A_i }{A_{ {\rm{i} } + k} } } \) (i=0, 1, 2, 3, …) einen n,k-Stern (für i+k > n ist n zu subtrahieren). Die Abbildungen zeigen einen 8,2-Stern und einen 5,2-Stern.
Alle Zacken: Welche Bedingung muss für n und k gelten, damit der n,k-Stern mit einem Streckenzug ohne erneut anzusetzen n Zacken hat?
n und k müssen teilerfremd sein.
Seien n und k teilerfremd und k' die kleinere der beiden Zahlen k und n-k.
Begründen Sie: Ein Schiff, das den Kurs eines n,k-Sterns durchfährt bis es wieder in seiner Startposition steht, dreht sich dabei k'-mal um seine eigene Achse.
Die Zahlenpaare (Anzahl der Kursänderungen |volle Drehungen um die Schiffsachse) sind quotientengleich. Ein derartiges Zahlenpaar ist \(\left( {\frac{n}{ {k'} }|1} \right)\). Dann ist auch (n|k') ein solches Zahlenpaar. Nach n Kursänderungen hat das Schiff k' Drehungen um die eigene Achse gemacht.
Sei α der Zackenwinkel (das ist der an jeder Zacke gleiche Winkel, siehe Abbildung) eines n,k-Sterns. Zeigen Sie: Dann gilt \( α = \frac{180°(n-2k')}{n} \)
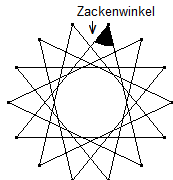
Aufgelöst nach α gilt: \( α = \frac{180°·(n-2k')}{n} \)
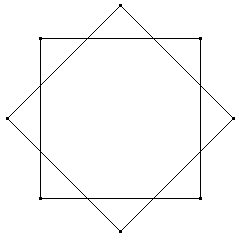
Zwölfeck aus 12 kongruenten Vierecken: Drei Seiten und eine Diagonale eines Vierecks seien gleichlang, die Länge der vierten sei das √2-fache jeder anderen Seitenlänge.
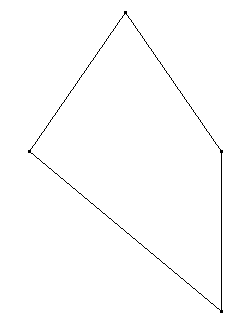
Zeigen Sie: 12 solche Vierecke parkettieren ein regelmäßiges Zwölfeck.
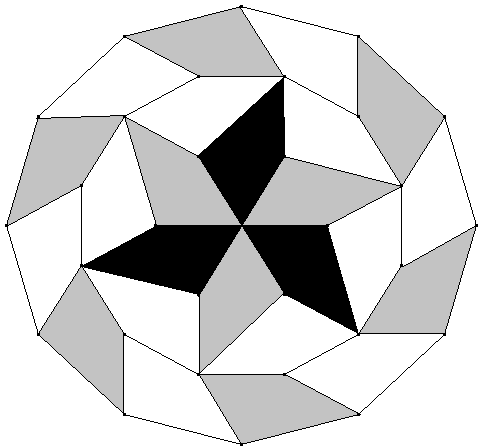
Zeigen Sie: 24 solche Vierecke parkettieren ein größeres regelmäßiges Zwölfeck.
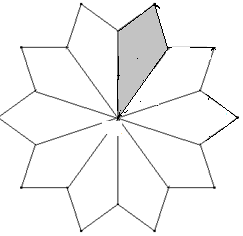
Ein 5,2-Stern:
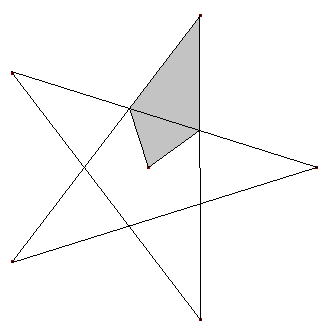
Welchen Umkreisradius hat ein aus 10 grauen Drachen (Abbildung) zusammengesetzter 10,3-Stern, wenn r der Umkreisradius des dargestellten 5,2-Sternes ist? Zeigen Sie: 12 solche Vierecke parkettieren ein regelmäßiges Zwölfeck.
Der 5,2-Stern kann in 5 Teile (grau unterlegt) zerteilt werden, von denen 10 zu einem 10,3-Stern zusammengesetzt werden können. Der Umkreisradius ist also der gleiche.