Lektion G31: Die 10 häufigsten Mathefehler
Du hast schon mal einen Flüchtigkeitsfehler gemacht und dadurch eine schlechte Note im Mathetest bekommen? In diesem Video stellen wir die häufigsten Mathefehler von Schülern vor. Diese Fehler kosten meist wertvolle Punkte und führen dazu, dass die Noten von Schülern schlechter ausfallen.
Zu diesen Fehler gehören unter anderen: Falsches Quadrieren, fehlerhaftes Bruchrechnen und Kürzen, Vorzeichenfehler, Terme nicht korrekt einsetzen, Klammerfehler, Potenz- und Wurzelregeln falsch anwenden.
Die 10 häufigsten Mathefehler - und wie ihr sie vermeidet!
In diesem Video stellen wir die häufigsten Mathefehler von Schülern vor. Diese Fehler kosten meist wertvolle Punkte und führen dazu, dass die Noten von Schülern schlechter ausfallen.
Zugriff auf Video nur als eingeloggter Benutzer.
Eine Auswahl an Programmen, die zu den Themengebieten der Fehler passen:
-
 Binomische Formel (1)Die 1. Binomische Formel wird hier grafisch veranschaulicht. Die Fläche (a+b)² entspricht der Fläche a²+2·ab+b².
Binomische Formel (1)Die 1. Binomische Formel wird hier grafisch veranschaulicht. Die Fläche (a+b)² entspricht der Fläche a²+2·ab+b². -
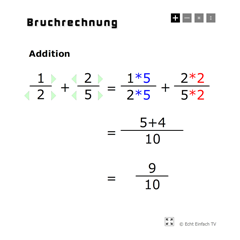 Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen.
Bruchrechnung (Grundrechenarten)Die vier Grundrechenarten bei beliebigen Brüchen mit Rechenweg, inklusive Erweitern und Kürzen. -
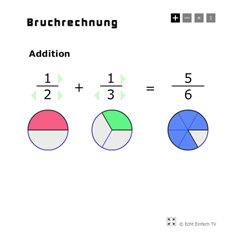 Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden.
Bruchrechnung (als Flächen)Mit diesem Programm könnt ihr beliebige Brüche berechnen, die gleichzeitig als Flächen angezeigt werden.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.
