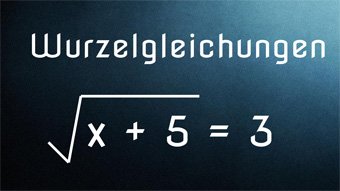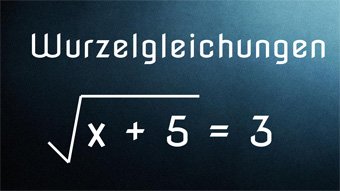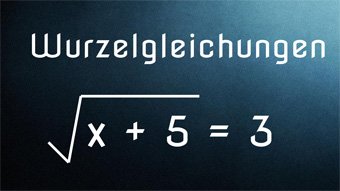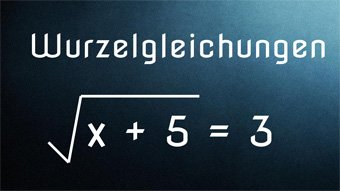Lektion G28: Wurzelgleichungen
Die Lektion Wurzelgleichungen besteht aus 5 Mathe-Videos, in denen wir euch zeigen, wie ihr Wurzelgleichungen schnell lösen könnt und auf welche Besonderheiten ihr beim Lösen achten müsst. Zusätzlich wird im Teil 5 erklärt, wie der Wert einer Wurzel berechnet werden kann.
Wurzelgleichungen - Einführung, Definitionsmenge
Wiederholung der wichtigsten Regeln zu den Wurzeln. Einführung Wurzelgleichung und Lösung von 3 = √(x+5) mittels Quadrieren. Definitionsmenge festlegen, da Radikand nicht negativ werden darf. Pflichtprobe bei Wurzeln. Lösung der Wurzelgleichungen √(3·x) = √(14+x) und √(15-2·x) + 1 = 3,5 mit Proben.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G28-2 Wurzelgleichungen - Lösen mit p-q-Formel, Wurzel-AmbiguitätLösung der Wurzelgleichung 1+x=√(4-x) mit Hilfe der p-q-Formel. Ambiguität (Zweideutigkeit) der Wurzel und Scheinlösungen. Lösungsmenge bei Wurzelgleichungen. Quadratwurzel führt immer zu postivem Ergebnis.
-
G28-3 Wurzelgleichungen - Lösungsschritte, Lösen mit GraphenLösungsschritte für Wurzelgleichungen. Lösung der Gleichung 4·√(x)=100 sowie 3·√(x-16)=√(20+x) und √(3+x)=x+5. Wurzelgleichungen lösen über Deutung als Funktionsgraphen und Schnittpunkt finden. Lösung von √(3+x)=x über Funktionsgraphen.
-
G28-4 Wurzelgleichungen - Verschachtelte Wurzeln, 4. WurzelLösung einer Wurzelgleichung mit verschachtelter Wurzel: √(-x + √(-x+5)) = 4 mit p-q-Formel. Lösung einer Gleichung mit 4. Wurzel: √(3x+3)=⁴√(-9x) mit Potenzierung. Wurzelgleichung mit 2. und 3. Wurzel durch Umwandlung in Potenzen.
-
G28-5 Wurzelgleichungen - Wurzeln selbst berechnenWurzeln mittels Intervallschachtelung berechnen, Methode 1: Annäherung an die Grenze über weitere Nachkommastellen, Methode 2: Annäherung über den Mittelwert aus den Grenzen. Heron-Verfahren zur Bestimmung des Wurzelwertes inklusive geometrischer Deutung.
Im Folgenden findet ihr einige Lernprogramme zu Wurzeln, mit denen ihr euer Wissen testen könnt:
-
 WurzelnHier können Wurzeln berechnt werden. Die Probe erfolgt mit Hilfe des Potenzierens. Wurzelexponent und Radikand dürft ihr frei wählen.
WurzelnHier können Wurzeln berechnt werden. Die Probe erfolgt mit Hilfe des Potenzierens. Wurzelexponent und Radikand dürft ihr frei wählen. -
 Wurzelwert berechnen (Heron-Verfahren)Dieses Programm zeigt, wie man sich dem Wurzelwert aus einer natürlichen Zahl annähern kann (Quadratwurzel).
Wurzelwert berechnen (Heron-Verfahren)Dieses Programm zeigt, wie man sich dem Wurzelwert aus einer natürlichen Zahl annähern kann (Quadratwurzel). -
 Wurzelwert berechnen (Intervallschachtelung)Dieses Programm nähert sich dem Wert einer Wurzel mittels Intervallschachtelung an.
Wurzelwert berechnen (Intervallschachtelung)Dieses Programm nähert sich dem Wert einer Wurzel mittels Intervallschachtelung an. -
 WurzelrechnerDer Wurzelrechner berechnet euch jede Wurzel. Gebt Wurzelexponent, Radikand oder Wurzelwert ein.
WurzelrechnerDer Wurzelrechner berechnet euch jede Wurzel. Gebt Wurzelexponent, Radikand oder Wurzelwert ein.
Hier findest du 4 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Wurzelgleichungen - Einführung
- Einfache Wurzelgleichungen lösen
- Wurzelgleichung lösen: 3 = √(x+5)
- Wurzelgleichung lösen: √(3x) = √(14+x)
- Wurzelgleichung lösen: √(15-2x)+1 = 3,5
- Wurzelgleichung lösen: 4·√x = 100
- Wurzelgleichung lösen: 3√(x-16) = √(20+x)
- Wurzelgleichungen grafisch lösen
- Ausschließen von Scheinlösungen bei Wurzelgleichungen
- Wurzelgleichungen: Scheinlösungen bei 1+x = √(4-x)
- Wurzelgleichungen: Scheinlösungen bei √(x+20) = -5
- Wurzelgleichungen: Scheinlösungen bei √(2x) = √(x-1)
- Ambiguität beim Wurzelziehen bei Gleichungen
- Verschachtelte Wurzeln lösen
- Verschachtelte Wurzeln lösen: √(-x+√(-x+5))=4
- Verschachtelte Wurzeln lösen: √(3x+3) = ⁴√(-9x)
- Verschachtelte Wurzeln lösen: {³√a·√a}/{³√(a^½):³√a⁴}=49
Häufige Fragen:
- Verlässliche Probe bei Wurzelgleichungen?
- Gleichung mit Wurzeln: Wurzel aus (13-4x) + x =2
- Rechnen mit Wurzeln, Gleichung lösen: (x-7) / √(2-1) + 7 + (3x) / √(2+1) = 0
- Lösung der Wurzelgleichung: √(x² + 5) = x + 1
- Löse die Quadratwurzelgleichung √(3x+4) - √(x+2) = √(x-3)
Finde weitere Fragen und Antworten in der Mathelounge.