Lektion G20: Zinseszins und Zinseszinsformel
In dieser Lektion schauen wir uns die Zinseszinsrechnung an, eine mehrfache Verzinsung über mehrere Jahre. Dazu klären wir im ersten Video, was Zinseszins überhaupt bedeutet und berechnen eine Beispielaufgabe. Im zweiten Teil leiten wir dann die Zinseszinsformel verständlich her.
Um die Inhalte verstehen zu können, ist es hilfreich, wenn ihr die Lektionen Prozente, Zinsrechnung und Potenzen gesehen habt.
Zinseszins - Einführung
Verzinsung von Kapital und Zinsen über mehrere Jahre, Anwendung der Zinseszinsformel zur direkten Berechnung des Endkapitals aus Startkapital, Zinssatz und Anzahl an Jahren.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G20-2 Zinseszins - ZinseszinsformelAusführliche Herleitung der Zinseszinsformel unter Nutzung der Prozent- und Potenzgesetze, Anwendung bei Beispielaufgabe mit nachvollziehbarem Lösungsweg.
-
 ZinseszinsDer Zins über mehrere Jahre kann schnell mit Hilfe der Zinseszinsformel berechnet werden. Alle Werte können belieibig festgelegt werden.
ZinseszinsDer Zins über mehrere Jahre kann schnell mit Hilfe der Zinseszinsformel berechnet werden. Alle Werte können belieibig festgelegt werden. -
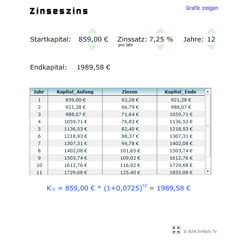 Zinseszins (Tabelle und Diagramm)Die Verzinsung über mehrere Jahre mit Auflistung des jeweiligen Kapitals und der Zinsen pro Jahr. Unten seht ihr die Zinseszinsformel (die Abkürzung, um auf das Endkapital zu kommen).
Zinseszins (Tabelle und Diagramm)Die Verzinsung über mehrere Jahre mit Auflistung des jeweiligen Kapitals und der Zinsen pro Jahr. Unten seht ihr die Zinseszinsformel (die Abkürzung, um auf das Endkapital zu kommen). -
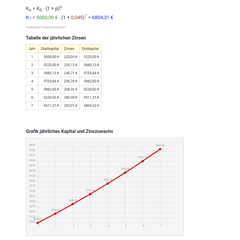 Rechner: ZinseszinsRechner für Zinseszins. Gib Startkapital, Zinssatz, Jahre oder Endkapital ein (drei Werte), der fehlende Wert wird automatisch berechnet inklusive Zinstabelle und Grafik.
Rechner: ZinseszinsRechner für Zinseszins. Gib Startkapital, Zinssatz, Jahre oder Endkapital ein (drei Werte), der fehlende Wert wird automatisch berechnet inklusive Zinstabelle und Grafik.
Hier findest du 6 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
- Festgeld mit monatlichen Zinssatz (Zinseszins) - reicht das Geld fürs Studium?
- Einfache Verzinsung oder Zinsesverzinsung?
- Kürzere Zinseszinsformel für direkte Berechnung der Zinsen?
- Finanzmathematik. Eine in acht Jahren fällige Schuld von 50.000 € soll bereits heute abbezahlt werden.
- Frau G. und Herr N. haben vor genau vier Jahren Geld in Aktien angelegt....
- Prozentrechnung mit Zinseszins: Im Schnitt jährlich 7% mehr Schrottautos?
Finde weitere Fragen und Antworten in der Mathelounge.

