CHECK: Logarithmus III
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Berechne den Logarithmus-Ausdruck \( \log_{2}{-16} \) ohne Taschenrechner.
Der Numerus muss stets größer als 0 sein.
Berechne den Logarithmus-Ausdruck \( \log_{3}{\frac{1}{27}} \) ohne Taschenrechner.
\( log_{3}(\frac{1}{27}) = \log_{3}(1) - \log_{3}(27) = 0 - \log_{3}(3^3) = -3·\log_{3}(3) = -3·1 = -3 \)
Berechne den Logarithmus-Ausdruck \( \log_{8}{2} \) ohne Taschenrechner.
Mit \( 2 = 8^\frac{1}{3} \) bzw. \( 2 = \sqrt[3]{8} \)
\( \log_{8} 2 = \log_{8}(8^\frac{1}{3}) = \frac{1}{3}·\log_{8}8 = \frac{1}{3}·1 = \frac{1}{3} \)
Berechne den Logarithmus-Ausdruck \( \log_{4}{2} \) ohne Taschenrechner.
Mit \( 2 = 4^\frac{1}{2} \)
\( \log_{4}(2) = \log_{4}(4^\frac{1}{2}) = \frac{1}{2}·\log_{4}(4) = \frac{1}{2}·1 = \frac{1}{2} \)
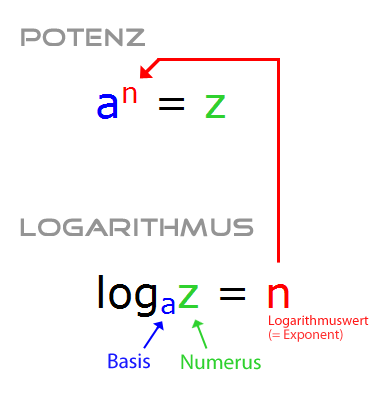
Bezeichnung beim Logarithmus: Wie nennt man a bei \( \log_{\textcolor{#F00}{a}}(z) \)?
Fortschritt:
