CHECK: Pythagoras im Alltag
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Die Diagonale eines quadratischen Tisches ist 120 cm. Berechne die Seitenlänge des Tisches.
Die Seiten sind jeweils a lang. Die Diagonale ist die Hypotenuse:
a² + a² = (120 cm)²
2·a² = 120² cm²
a² = 14400/2 cm²
a = √7200 cm
Max nimmt einen Faden und legt ihn so auf den Tisch, dass sich ein Dreieck ergibt. Er misst die Dreiecksseiten und erhält: a = 8 cm, b = 6 cm und c = 10 cm. Handelt es sich um ein rechtwinkliges Dreieck?
Für ein rechtwinkliges Dreieck muss gelten a² + b² = c².
c² = 6² + 8² = 64 + 36 = 100 cm²
c = √100
c = 10 cm
Die Gleichung stimmt, also liegt ein rechtwinkliges Dreieck vor.
Untersuche, ob es möglich ist, eine 5,2 m lange und 2,1 m breite rechteckige Holzplatte durch eine Tür zu transportieren, die 2 m hoch und 80 cm breit ist. Passt die Holzplatte durch die Tür?
Die Diagonale der Tür beträgt:
c = √(2² + 0,8²) m = 2,15 m
Da die Platte nur 2,10 m breit ist, sollte das kein Problem sein (Die Platte darf nicht all zu dick sein.)
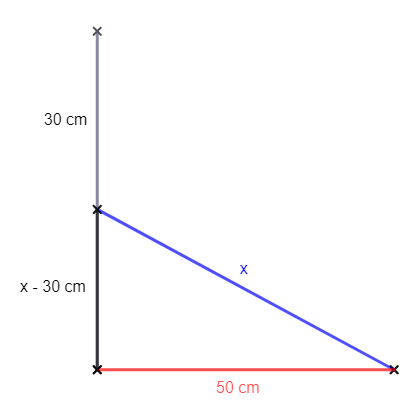
Ein senkrecht an der Wand stehender Stab rutscht 30 cm herunter. Dabei entfernt sich das untere Ende des Stabes einen halben Meter von der Mauer. Wie lang ist der Stab?
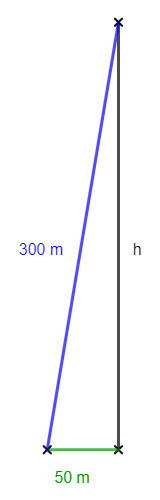
Ein Fesselballon befindet sich senkrecht über seinem Befestigungspunkt und ist an einem 300 m langen, voll gespannten Seil befestigt. Durch starken Wind wird er 50 m weit abgetrieben. In welcher Höhe befindet er sich jetzt?
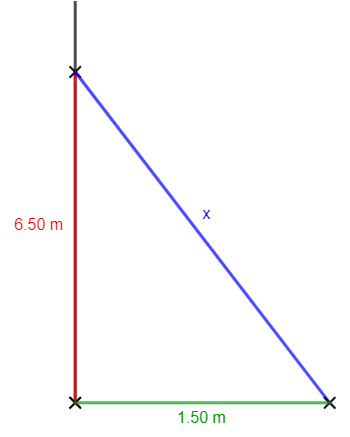
Wie lang muss eine Leiter sein, wenn sie bei einem Abstand von 1,50 m von einer Wand 6,50 m hoch sein soll?
Bei einem gleichseitigen Dreieck sei jede Seite x lang. Wie groß ist die Höhe h bezüglich x?
Stellen wir die Formel für die Höhe h in Bezug auf x auf:
x² = (0,5x)² + h²
x² = 0,25x² + h² |-0,25x²
0,75x² = h²
h = √(0,75x²) = √0,75·x
Fortschritt: