CHECK: Pythagoras Gemischtes I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Wie lautet der Satz des Pythagoras? Die Hypotenuse ist c. Achtung: Wir haben ihn ein wenig umgeformt.
\( a^2 + b^2 = c^2 \quad | \sqrt{\phantom{x}} \\ \sqrt{c^2} = \sqrt{a^2 + b^2} \\ c = \sqrt{a^2 + b^2} \)
Berechne die Breite des Rechtecks mit Hilfe vom Satz des Pythagoras.
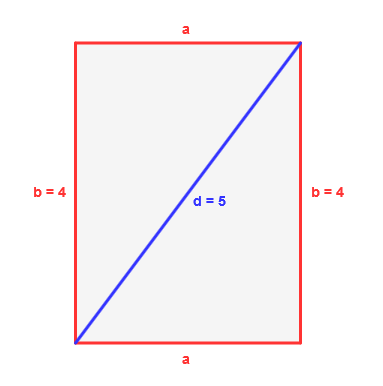
Die Länge b beträgt 4 cm. Die Diagonale d misst 5 cm. Wie lang ist Breite a?
Das Rechteck wird durch die Diagonale in zwei rechtwinklige Dreiecke geteilt. Für diese können wir den Satz des Pythagoras aufstellen:
a² + b² = d²
Umgestellt nach a:
a² + b² = d² | - b²
a² = d² - b² | Wurzel ziehen √
√a² = √(d² - b²)
a = √(d² - b²)
Nun noch die Werte einsetzen:
a = √(d² - b²) | d = 5 cm, b = 4 cm
a = √(5² - 4²) cm²
a = √(25 - 16) cm²
a = √9 cm²
a = 3 cm
Wie lautet die Formel für die Länge der Raumdiagonale d bei einem Quader mit den Kantenlängen a, b und c.
Formel für d (denkt euch die Diagonale x auf dem Boden):
d² = x² + c²
Und x können wir ermitteln mit a und b:
x² = a² + b²
Nun x² in die erste Formel einsetzen:
d² = x² + c² | x² = a² + b²
d² = (a² + b²) + c²
d² = a² + b² + c²
\( d = \sqrt{a^2 + b^2 + c^2} \)
Ein rechtwinkliges Dreieck ABC mit den Katheten a = 3 cm und b = 4 cm ist gegeben. Wie lang ist die Hypotenuse c?
Die Katheten quadriert und addiert ergeben zusammen das Quadrat der Hypotenuse, demnach ist der Satz des Pythagoras hier:
$$ a^2 +b^2 = c^2 $$
Wir suchen die Seite c, müssen deshalb noch die Wurzel ziehen:
$$ c = \sqrt {a^2+b^2 } $$
Jetzt können die Werte eingesetzt werden:
$$ c = \sqrt {(3 \;cm)^2 + (4 \;cm)^2 } \\ c = \sqrt {25 \;cm^2} \\ c = 5 \;cm $$
Übrigens: Die Zahlen {3, 4, 5} zusammen bilden ein sogenanntes Pythagoreisches Tripel.
Welches ist die korrekte Schreibweise für den „Satz des …“?
Der griechische Philosoph und Mathematiker hieß Pythagoras von Samos. Er lebte übrigens 570 vor Christus bis 510 vor Christus.
Berechne die Länge der Hypotenuse in einem rechtwinkligen Dreieck, wenn die Katheten a = 15,4 cm und b = 1,78 dm lang sind. Runde das Ergebnis auf zwei Nachkommastellen.
Der Satz des Pythagoras besagt:
c² = a² + b²
wobei c die Hypotenuse ist, also mit b = 17,8 cm
c = \( \sqrt{15,4^2 + 17,8^2} \) cm = 23,54 cm
Die Hypotenuse hat also eine Länge von rund 23,54 cm.
Es liegt ein gleichseitiges Dreieck vor. Die Höhe sei 10 cm, wie lang ist eine Dreiecksseite a ungefähr?
In dem gleichseitigen Dreieck gilt:
a² = (\( \frac{1}{2} \)·a)² + h²
a² = (\( \frac{1}{2} \)·a)² + (10 cm)²
a² = \( \frac{1}{4} \)·a² + (10 cm)²
\( \frac{3}{4} \) · a² = 100 cm²
a² = 100 cm² · \( \frac{4}{3} \)
a = \( \sqrt{ \frac{400}{3} \;cm^2 } \)
a ≈ 11,55 cm
Fortschritt: