CHECK: Quader I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Wie viele Kanten hat ein Quader?
Zähle die Kanten in der 3D-Darstellung:
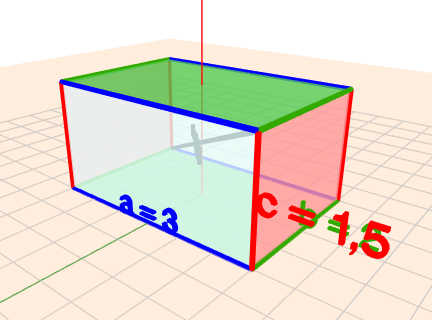
4 blaue + 4 rote + 4 grüne = 12 Kanten
Wie viele Ecken hat ein Quader?
8 Ecken. Zum Beispiel zu merken als 4 oben und 4 unten.
Welche Flächen des Quaders bilden die Mantelfäche?
Die Mantelfäche ist die umliegende Fläche. Beim Quader sind dies 4 Seitenflächen.
Wieviele Diagonalen hat ein Quader insgesamt? Berücksichtige alle Flächendiagonalen und Raumdiagonalen.
12 Diagonalen in den Außenflächen und 4 Raumdiagonalen.
Welche Aussage trifft für einen Quader nicht zu?
Gegenüberliegende Flächen sind beim Quader immer parallel, genau wie die gegenüberliegenden Kanten.
Fortschritt:
