Wissen: Satz des Thales, Höhensatz und Kathetensatz des Euklid

Satz des Thales

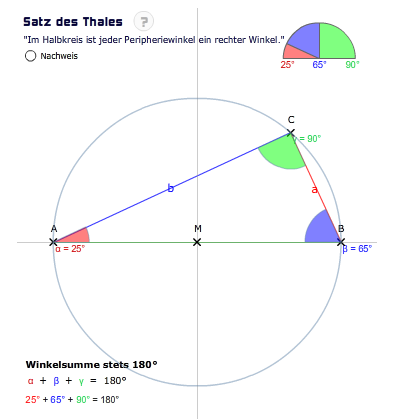
Der Satz des Thales besagt: Es ergibt sich stets ein rechtwinkliges Dreieck, wenn man den Durchmesser des Kreises als Grundseite betrachtet und einen weiteren Dreieckspunkt auf die Kreislinie setzt. Eine alternative Formulierung lautet: Im Halbkreis ist jeder Peripheriewinkel ein rechter Winkel. Oder: Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.

Berechnung der Dreiecksfläche über die Höhe

Neben der oben gezeigten Flächenformel für Rechtwinklige Dreiecke (A = a·b:2) existiert eine weitere Formel, die im Video hergeleitet wird und nachfolgend illustriert ist:

Höhensatz des Euklid (Höhenformeln fürs Rechtwinklige Dreieck)

Sofern wir die Höhe ermitteln sollen, stehen uns zwei Formeln zur Verfügung, die wir ebenfalls im Video herleiten. Wir können die Höhe bereits ermitteln, wenn uns die Dreiecksseiten a, b und c gegeben sind. Genauso können wir die Höhe berechnen, wenn wir die Teilstrecken p und q kennen:

Die Formel h² = q·p bezeichnet man auch als Höhensatz des Euklid. Die Herleitung sei im Folgenden aufgeführt, für die Bezeichnung der Unbekannten vergleiche obige Dreiecksgrafik:

p² = a² - h² → a² = p² + h²

q² = b² - h² → b² = q² + h²

Satz des Pythagoras:

a² + b² = c²   | Einsetzen der Formeln für a² und b²

(p² + h²) + (q² + h²) = c²

p² + h² + q² + h² = c²

p² + q² + 2·h² = c²   | c ergibt sich aus (p+q)

p² + q² + 2·h² = (p+q)²

p² + q² + 2·h² = p² + 2·p·q + q²

p² + q² + 2·h² = p² + 2·p·q + q²   | -q² - p²

2·h² = 2·p·q   | :2

h² = p·q

Kathetensatz des Euklid

Erinnern wir uns, die Katheten sind die beiden kurzen Seiten des Dreiecks, also Seiten a und b. Wenn wir die Höhe auf c einzeichnen, erhalten wir die folgende bereits bekannte Grafik:

Es sind zwei kleine rechtwinklige Dreiecke entstanden, auf die wir nun den Satz des Pythagoras anwenden könnnen:

a² = p² + h²   | für h² setzen wir den Höhensatz von oben ein mit h²=p·q

a² = p² + (p·q)   | p ausklammern

a² = p · (p + q)   | (p+q) ist ja c, also ersetzen wir den Term mit c

a² = p · c   | das ist der 1. Teil des Kathetensatzes

Nun betrachten wir das zweite kleine Dreieck:

b² = q² + h²   | für h² setzen wir den Höhensatz von oben ein mit h²=p·q

b² = q² + (p·q)   | q ausklammern

b² = q · (q + p)   | (q+p) ist ja c, also ersetzen wir den Term mit c

b² = q · c   | das ist der 2. Teil des Kathetensatzes

Höhensatz und Kathetensatz des Euklid in einer Grafik: