Lektion F01: Kartesisches Koordinatensystem
In dieser Lektion bringen wir euch bei, wie das Koordinatensystem aufgebaut ist, was Koordinaten überhaupt sind und wofür man sie benutzen kann.
Kartesisches Koordinatensystem
Einführung ins Kartesische Koordinatensystem. Wir betrachten uns x-Achse (Abszisse) und y-Achse (Ordinate), Punkte mit Koordinaten und die vier Quadranten.
Zugriff auf Video nur als eingeloggter Benutzer.
Mit den folgenden Programmen könnt ihr das kartesische Koordinatensystem ausprobieren und besser kennen lernen. Bewegt die Maus und seht die x- und y-Koordinate direkt am Punkt P.
-
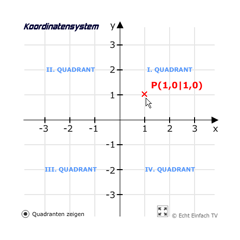 KoordinatensystemBewegt die Maus im Koordinatensystem und seht die Koordinaten für x und y direkt am Punkt P. Werte gerundet. Klickt einmal mit der Maus und erhaltet genauere Werte.
KoordinatensystemBewegt die Maus im Koordinatensystem und seht die Koordinaten für x und y direkt am Punkt P. Werte gerundet. Klickt einmal mit der Maus und erhaltet genauere Werte. -
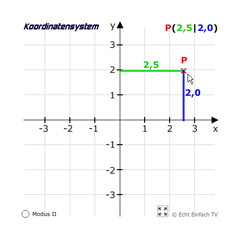 Koordinatensystem (Linien)Hier sind Höhe und Breite als farbige Linien eingezeichnet. Klickt auf Modus II, um die Position der Linien zu ändern. Sie liegen dann direkt auf den Achsen des Koordinatensystems.
Koordinatensystem (Linien)Hier sind Höhe und Breite als farbige Linien eingezeichnet. Klickt auf Modus II, um die Position der Linien zu ändern. Sie liegen dann direkt auf den Achsen des Koordinatensystems.
Hier findest du 3 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.
