Lektion G03: Distributivgesetz
In der letzten Lektion hatten wir uns Kommutativgesetz und Assoziativgesetz betrachtet. Nun kommen wir zum nächsten Rechengesetz, dem Distributivgesetz, das häufig in der Mathematik angewendet wird. Es gehört zu den Grundlagen, die ihr auf jeden Fall beherrschen müsst. Übrigens heißt 'distribuere' (lateinisch) so viel wie "verteilen". Wieso das so ist, seht ihr im Folgenden.
Distributivgesetz
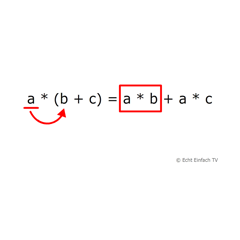
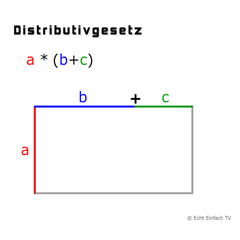
Eine der wichtigsten Rechenregeln der Mathematik ist das Distributivgesetz. Es lautet a · (b + c) = a · b + a · c. Wir können es auch um weitere Summanden erweitern, zum Beispiel: a · (b + c + d) = a · b + a · c + a·d
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
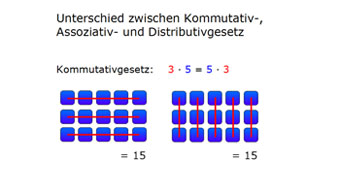
G03-2 Unterschied Kommutativ-, Assoziativ- und DistributivgesetzWir zeigen euch, was der Unterschied zwischen Kommutativgesetz, Assoziativgesetz und Distributivgesetz ist. Dabei stellen wir alle 3 Rechengesetze grafisch dar.
Hier findest du 3 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Häufige Fragen:
Finde weitere Fragen und Antworten in der Mathelounge.