Lektion G27: Kubische Gleichungen und Polynomdivision
Das Lösen von kubischen Gleichungen ist für manche Schüler eine große Herausforderung. Wir helfen euch und zeigen, welche Lösungsverfahren es gibt und wie ihr diese sicher anwendet.
Insbesondere schauen wir uns die Polynomdivision an, die beim Lösen von kubischen Gleichungen hilft, denn sie macht aus einer Gleichung 3. Grades eine Gleichung 2. Grades (also x³ → x²). Und diese Gleichung können wir dann mit Hilfe der p-q-Formel lösen.
Sinnvoll ist es, wenn ihr die Videos zu den quadratischen Gleichungen gesehen habt.
Am Ende dieser Lektion werdet ihr in der Lage sein, kubische Gleichungen zu lösen (insbesondere mit Hilfe der Polynomdivision).
Kubische Gleichungen - Einführung
Bedeutung "kubisch". Allgemeinform und Normalform der kubischen Gleichung (Gleichungen 3. Grades), Auflistung von Lösungsverfahren, Anzahl von Lösungen (bzw. Nullstellen bei Deutung als Funktion), was ist ein Polynom und ein Monom, Einleitung zur Division von Polynomen.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
G27-2 Polynomdivision - Anwendung des VerfahrensLösungsverfahren Polynomdivision, das den Grad des Polynoms vermindert, Wiederholung schriftliche Division, Einführung zum Verfahren der Polynomdivision am Beispiel (x²-4x-5):(x-5)
-
G27-3 Polynomdivision - Erklärung des VerfahrensWir erklären, warum die Polynomdivision funktioniert bzw. wie Polynome dividiert werden. Darstellung der Division als Bruch, Umformung mittels Erweitern des Zählers sowie Ergänzung des Zählerterms und anschließendes Kürzen.
-
G27-4 Kubische Gleichungen - LösungsverfahrenLösung von (x³+6x²+11x+6):(x+1) mit Polynomdivision und p-q-Formel. Polynom in Linearfaktorform, Deutung als Funktionen. Lösen über Ausklammern.
-
G27-5 Kubische Gleichungen - LösungsverfahrenLösen mit Wurzel bei reinkubischen Gleichungen. Erklärung der Polynomdivision mit Rest. Lösungsmenge Reelle und Komplexe Zahlen.
-
G27-6 Gleichung 3. Grades lösen mit Polynomdivision und pq-FormelAnwendung des neuen Wissens: Zuerst raten wir systematisch die erste Lösung der Gleichung x³-6x²+11x-6=0, danach wenden wir die Polynomdivision an und erhalten einen Term zweiten Grades, der null gesetzt wird und sich mit der pq-Formel lösen lässt.
Beim ersten Matheprogramm könnt ihr eigene kubische Gleichungen eingeben, es berechnet euch die Lösungen und stellt die Gleichung als Funktionsgraph dar. Nutzt es, um zum Beispiel die Lösungen eurer Hausaufgaben auf Richtigkeit zu kontrollieren. Zusätzlich könnt ihr mit dem zweiten Programm eure Lösungen überprüfen.
-
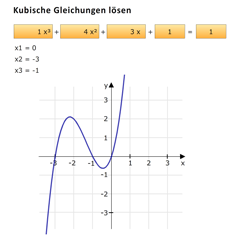 Kubische Gleichungen lösenDieses Programm löst beliebige kubische Gleichungen und stellt die Gleichung als Funktion dar (Nullstellen sind die Lösungen).
Kubische Gleichungen lösenDieses Programm löst beliebige kubische Gleichungen und stellt die Gleichung als Funktion dar (Nullstellen sind die Lösungen). -
 Kubische Gleichung RechnerEinfach eine beliebige Kubische Gleichung eingeben und die Lösungen werden euch angezeigt. Reelle und Komplexe Zahlen. Zur Berechnung werden die Cardanischen Formeln benutzt.
Kubische Gleichung RechnerEinfach eine beliebige Kubische Gleichung eingeben und die Lösungen werden euch angezeigt. Reelle und Komplexe Zahlen. Zur Berechnung werden die Cardanischen Formeln benutzt.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.
Artikel im Wiki:
- Kubische Gleichungen - Einführung
- Kubische Gleichungen Lösungsverfahren
- Was ist ein Polynom?
- Polynomdivision
- Polynomdivision erklärt
- Verfahren der Polynomdivision
- Raten einer Nullstelle für Polynomdivision
- Polynomdivision mit Rest
- Kubische Gleichung mit Polynomdivision lösen
- Kubische Gleichungen grafisch lösen
- Besondere Fälle kubischer Gleichungen





