Lektion G06: Rechnen mit Vorzeichen
Einigen Schülern bereitet das Rechnen mit negativen Zahlen Probleme, daher schauen wir uns heute das Rechnen mit Vorzeichen an. Ihr lernt, wie ihr Addition, Subtraktion, Multiplikation und Division sicher mit Vorzeichen durchführen könnt. Dies ist Grundlagen-Wissen der Mathematik, das ihr beherrschen müsst. Wir bewegen uns übrigens im Bereich der ganzen Zahlen.
Rechnen mit Vorzeichen - Addition und Subtraktion
Einführung zum Rechnen mit Vorzeichen, Addition und Subtraktion positiver und negativer Zahlen, Herleitung der Rechenregeln, Grundlagen-Wissen Mathematik.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
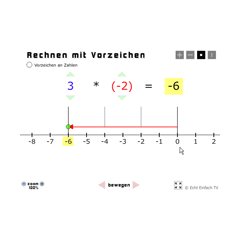
G06-2 Rechnen mit Vorzeichen - Multiplikation und DivisionErläuterung der Rechenregeln zur Multiplikation und Division mit positiven und negativen Zahlen, mehrere Beispielaufgaben zum sicheren Rechnen.
Mathematik-Programm zum Ausprobieren und zum Selbsttest:
-
Grundrechenarten (Ganze Zahlen)Grundrechenarten bei den Ganzen Zahlen: Addition, Subtraktion, Multiplikation und Division. -
Rechnen mit VorzeichenDas Rechnen mit Vorzeichen am Zahlenstrahl grafisch verdeutlicht!
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
- Wann schreibe ich (-3)² und wann -(3²)?
- Rechnen mit Negativen Zahlen: -4 +(-2) =?
- Warum ergibt eine negative Zahl mit einer negativen Zahl multipliziert ein positives Ergebnis?
Finde weitere Fragen und Antworten in der Mathelounge.