Lektion TRI05: Einheitskreis
Nachdem wir uns in den letzten Lektionen die Dreiecksberechnung mit Sinus, Kosinus und Tangens angeschaut haben, gehen wir nun einen großen Schritt weiter: Wir betrachten sin, cos, tan am Einheitskreis. Damit können wir Sinus-, Kosinus- und Tangenswerte für alle beliebigen Winkel bestimmen und sind nicht mehr an Winkel von 0° bis 180° gebunden.
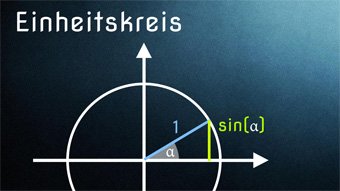
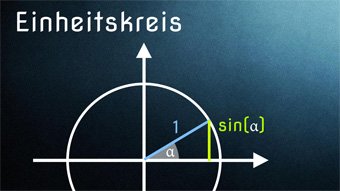
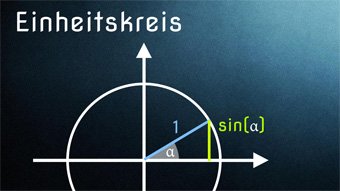
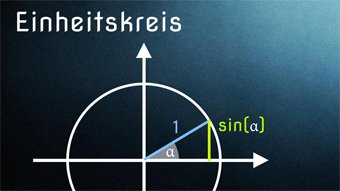
Einheitskreis - Einführung Einheitskreis mit Sinus und Kosinus
Einheitskreis zur Ermittlung von Sinus und Kosinus für beliebige Winkel. Wie können wir die Werte für sin und cos am Einheitskreis ablesen. Zusätzlich klären wir die Wortherkunft "Einheitskreis". Wir zeigen, wie ihr euch wichtige Sinus- und Kosinuswerte merken könnt.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
TRI05-2 Einheitskreis - Referenzdreieck, PunktkoordinatenWann sind Sinus und Kosinus positiv und negativ. Sinus und Kosinus lassen sich mit Referenzdreiecken für jeden Quadranten des Koordinatensystems bestimmen. Wertebereich für Sinus und Kosinus. (Ko)Sinus ablesen an den Punktkoordinaten des Winkels.
-
TRI05-3 Einheitskreis - Tangens am EinheitskreisTangens für beliebige Winkel mit Hilfe des Einheitskreises. Im Gegensatz zum Sinus und Kosinus kann der Tangens bei bestimmten Winkeln "nicht definiert" sein. Positive und negative Tangenswerte je nach Quadrant. Tangens mit Punktkoordinaten berechnen.
-
TRI05-4 Einheitskreis - Identitäten zur WinkelbestimmungWinkel (0° bis 360°) aus Sinus- und Kosinuswert bestimmen. Was sind Identitäten. Wir behandeln eine Auswahl an Identitäten inkl. Anwendung. Deutung des Kosinus als um 90° rotierter Sinus. Warum heißt Kosinus Ko-Sinus.
-
TRI05-5 Einheitskreis - Trigonometrischer PythagorasSchreibweise sin²(a) für (sin(a))². Herleitung des trigonometrischen Pythagoras: cos²(a) + sin²(a) = 1 sowie der Koordinatengleichung des Einheitskreises x² + y² = 1. Vom Winkel und Sinuswert rechnerisch zu dessen Kosinuswert.
-
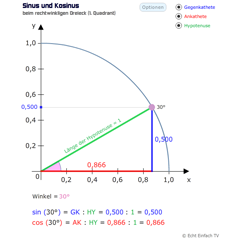 Sinus und Kosinus im 1. QuadrantLernt die Werte für Sinus und Kosinus von 0 bis 90 Grad. Der Wert für Sinus steht an der Gegenkathete, der Wert für Kosinus an der Ankathete. Nutzt auch die Koordinaten des Punktes auf dem Kreisbogen.
Sinus und Kosinus im 1. QuadrantLernt die Werte für Sinus und Kosinus von 0 bis 90 Grad. Der Wert für Sinus steht an der Gegenkathete, der Wert für Kosinus an der Ankathete. Nutzt auch die Koordinaten des Punktes auf dem Kreisbogen. -
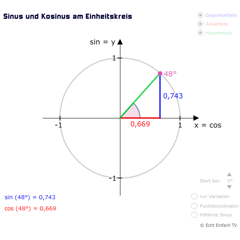 Einheitskreis: Sinus und KosinusHier werden Sinus und Kosinus am Einheitskreis veranschaulicht. Durch den Einheitskreis ist es möglich, (Ko)Sinuswerte für alle beliebigen Winkel zu bestimmen.
Einheitskreis: Sinus und KosinusHier werden Sinus und Kosinus am Einheitskreis veranschaulicht. Durch den Einheitskreis ist es möglich, (Ko)Sinuswerte für alle beliebigen Winkel zu bestimmen. -
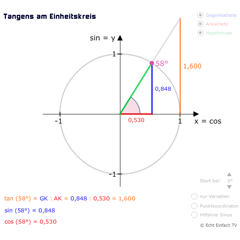 Einheitskreis: TangensHier wird der Tangens am Einheitskreis veranschaulicht. Der Tangens kann auch als Sinus durch Kosinus definiert werden. Bei bestimmten Winkeln ist der Tangens nicht definiert.
Einheitskreis: TangensHier wird der Tangens am Einheitskreis veranschaulicht. Der Tangens kann auch als Sinus durch Kosinus definiert werden. Bei bestimmten Winkeln ist der Tangens nicht definiert. -
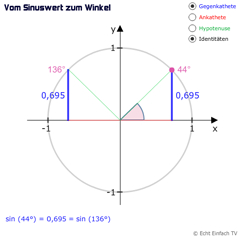 Einheitskreis: Vom (Ko)Sinuswert zum WinkelVeranschaulichung von einfachen Identitäten für Winkel von 0° bis 360°. Einem Sinuswert entsprechen 2 Winkel, einem Kosinuswert entsprechen 2 Winkel.
Einheitskreis: Vom (Ko)Sinuswert zum WinkelVeranschaulichung von einfachen Identitäten für Winkel von 0° bis 360°. Einem Sinuswert entsprechen 2 Winkel, einem Kosinuswert entsprechen 2 Winkel. -
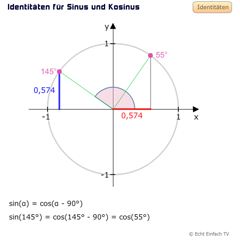 Einheitskreis: Identitäten für Sinus und Kosinus10 Identitäten können hier entdeckt und am Einheitskreis geübt werden. Mit Identitäten lassen sich weitere mögliche Winkel für (Ko)Sinuswerte ermitteln.
Einheitskreis: Identitäten für Sinus und Kosinus10 Identitäten können hier entdeckt und am Einheitskreis geübt werden. Mit Identitäten lassen sich weitere mögliche Winkel für (Ko)Sinuswerte ermitteln. -
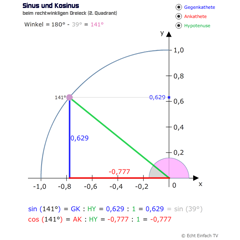 Sinus und Kosinus im 2. QuadrantDie Werte für Sinus und Kosinus von 90 bis 180 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete.
Sinus und Kosinus im 2. QuadrantDie Werte für Sinus und Kosinus von 90 bis 180 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete. -
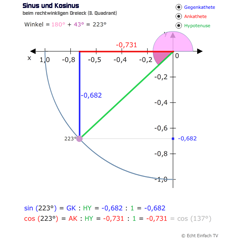 Sinus und Kosinus im 3. QuadrantDie Werte für Sinus und Kosinus von 180 bis 270 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete.
Sinus und Kosinus im 3. QuadrantDie Werte für Sinus und Kosinus von 180 bis 270 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete. -
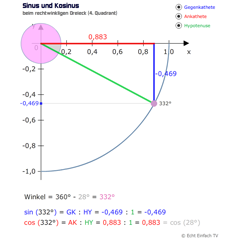 Sinus und Kosinus im 4. QuadrantDie Werte für Sinus und Kosinus von 270 bis 360 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete.
Sinus und Kosinus im 4. QuadrantDie Werte für Sinus und Kosinus von 270 bis 360 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete.
Hier findest du 2 Arbeitsblätter, mit denen du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Artikel im Wiki:
- Einheitskreis - Einführung
- Sinus und Kosinus am Einheitskreis
- Wichtige Sinus- und Kosinuswerte
- Tangenswerte am Einheitskreis
- Identitäten
- Identität: sin(α) = cos(90° - α)
- Identität: cos(α) = sin(90° - α)
- Identität sin(α) = cos(α - 90°)
- Identität sin(α) = -sin(-α)
- Identität cos(α) = cos(-α)
- Identität sin(90° + α) = sin(90° - α)
- Identität cos(90° + α) = -cos(90° - α)
- Identitäten sin(α) = sin(α + 360°) und cos(α) = cos(α + 360°)
- Warum Kosinus Ko-Sinus heißt
- Trigonometrischer Pythagoras
- Koordinatengleichung des Einheitskreises