Lektion TRI06: Trigonometrische Funktionen - Matheretter Die Videos erklären einfach, wie die Sinusfunktion entsteht und was die Sinusschwingung bedeutet. Nach der Einführung sehen wir uns die Kosinusfunktion und die Tangensfunktion an.
Matheretter

Lektion TRI06: Trigonometrische Funktionen

Inhalte:

  1. Was ist die Sinusfunktion?
  2. Wie hilft uns der Einheitskreis beim Zeichnen der Sinuskurve (also des Graphen der Sinusfunktion)?
  3. Wie ergibt sich die Kosinusfunktion und wie die Tangensfunktion?
  4. Was meint Periode bei den trigonometrischen Funktionen?
  5. Worin unterscheiden sich Sinus- und Kosinusfunktion von der Tangensfunktion grafisch?
  6. Wie verändert sich der Sinusgraph, wenn wir die Parameter der Funktionsgleichung f(x) = a·sin(b·x + c) + d verändern?
  7. Was sind Amplitude, (Kreis)Frequenz und Phasenverschiebung?
Voraussetzung:
Laut Lehrplan: 10. Klasse
Videos anschauen › Artikel lesen ›

Mit dem Wissen zum Einheitskreis sind wir nun in der Lage, einen Schritt weiter zu gehen. Wir treffen auf die elementaren Trigonometrischen Funktionen, also: 1. Sinusfunktion, 2. Kosinusfunktion, 3. Tangensfunktion.

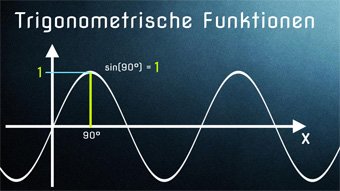
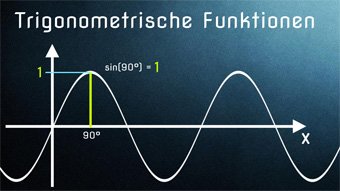
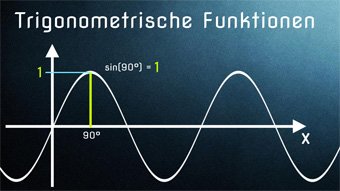
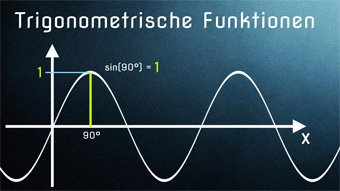
Vielleicht habt ihr euch auch schon immer gefragt, weshalb die Sinusschwingung so gekrümmt aussieht, eine einfache Erklärung bieten die Videos.

Trigonometrische Funktionen - Einführung Sinusfunktion

Was bedeutet Sinus-Funktion, wie ergibt sie sich? Wir stellen die Sinusfunktion im Koordinatensystem dar und erhalten einen geschwungenen Graphen (Sinuskurve). Beispiel aus dem Alltag: Beschreibung der Flughöhe eines Balles, der an einer Feder befestigt ist.

Zugriff auf Video nur als eingeloggter Benutzer.

Registrieren Einloggen

Weitere Videos für Kunden:

  • Abo
    Zugriff auf alle Videos
    TRI06-2 Trigonometrische Funktionen - Kosinusfunktion + Periode
    Wie ergibt sich die Kosinusfunktion? Einführung der Periode bei Sinus und Kosinus. Darstellung der (Ko)Sinusfunktion im Einheitskreis. Kosinus-Schwingung am Beispiel des Pendels! Lineare Bewegung kontra Kosinusschwingung.
  • Abo
    Zugriff auf alle Videos
    TRI06-3 Trigonometrische Funktionen - Tangensfunktion
    Wie ergibt sich die Tangensfunktion? Der Tangensgraph unterscheidet sich vom (Ko)Sinusgraphen. Auch klären wir, wie man die Periode der Sinus-, Kosinus- und Tangensfunktion notiert, für Sinus: sin(α) = sin(α + k·360°)
  • Abo
    Zugriff auf alle Videos
    TRI06-4 Trigonometrische Funktionen - Allgemeine Sinusfunktion
    Wie lässt sich die Sinusfunktion verändern? Wir betrachten die Funktionsgleichung f(x) = a·sin(b·x + c) + d und klären die Bedeutung der einzelnen Variablen. Wir strecken und stauchen den Sinusgraphen und spiegeln ihn.
  • Abo
    Zugriff auf alle Videos
    TRI06-5 Trigonometrische Funktionen - Kosinus- und Tangensfunktion
    Wir verschieben die Sinusfunktion entlang der Achsen und schauen uns an, wie sich die Kosinus- und Tangensfunktion verändern lassen. Auch klären wir in diesem Zusammenhang die Begriffe Amplitude, (Kreis)Frequenz und Phasenverschiebung.

Alle Videos bestellen

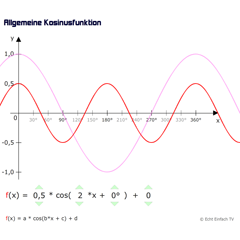  • Kosinusfunktion (allgemein)
    Kosinusfunktion (allgemein)
    Mit diesem Programm könnt ihr die allgemeine Kosinusfunktion der Form f(x) = a·cos(b·x + c) + d verändern. Die Änderungen am Graphen werden live angezeigt.
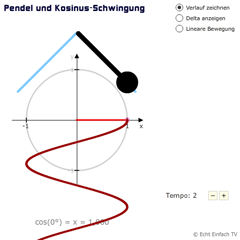  • Pendel und Kosinusschwingung
    Pendel und Kosinusschwingung
    Darstellung der Kosinusschwingung anhand eines Pendels. Zeichnet den Verlauf des Pendels ein und ihr erkennt die Kosinusschwingung. Die Pendelbewegung lässt sich auch linear einstellen.
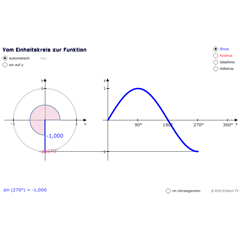  • Vom Einheitskreis zur (Ko)Sinusfunktion
    Vom Einheitskreis zur (Ko)Sinusfunktion
    Vom Einheitskreis zur Sinus- und Kosinusfunktion. Indem wir die Sinuswerte für jeden Winkel abtragen, erhalten wir die Sinusschwingung.
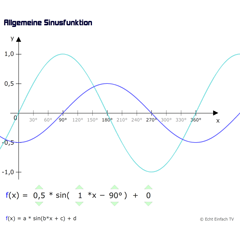  • Sinusfunktion (allgemein)
    Sinusfunktion (allgemein)
    Mit diesem Programm könnt ihr die allgemeine Sinusfunktion der Form f(x) = a·sin(b·x + c) + d verändern. Die Änderungen am Graphen werden live angezeigt.
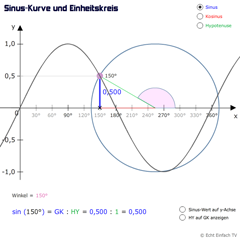  • Sinuskurve und bewegter Einheitskreis
    Sinuskurve und bewegter Einheitskreis
    Hier wird der Einheitskreis in die Sinuskurve eingezeichnet. Dies ist eine neuartige Variante, den Zusammenhang zwischen Einheitskreis und Sinuskurve darzustellen.
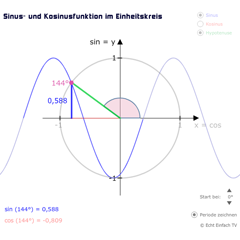  • Sinus- und Kosinusfunktion im Einheitskreis
    Sinus- und Kosinusfunktion im Einheitskreis
    Die Sinusfunktion (horizontal) und die Kosinusfunktion (vertikal) werden hier in den Einheitskreis eingezeichnet. Neue Variante, um den Zusammenhang darzustellen.
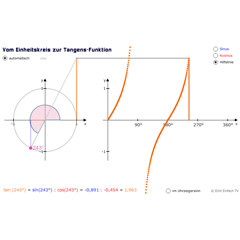  • Vom Einheitskreis zur Tangensfunktion
    Vom Einheitskreis zur Tangensfunktion
    Dieses Programm zeichnet die Tangenswerte vom Einheitskreis für den jeweiligen Winkel in ein zweites Koordinatensystem. So entsteht der Graph für Tangens.
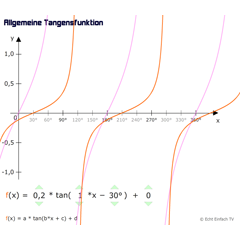  • Tangensfunktion (allgemein)
    Tangensfunktion (allgemein)
    Mit diesem Programm könnt ihr die allgemeine Tangensfunktion der Form f(x) = a·tan(b·x + c) + d verändern. Die Änderungen am Graphen werden live angezeigt.
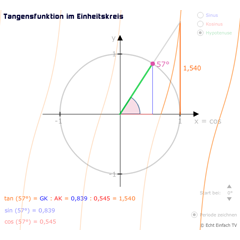  • Tangensfunktion im Einheitskreis
    Tangensfunktion im Einheitskreis
    Der Graph der Tangensfunktion wird hier in den Einheitskreis eingezeichnet. Dies ist eine neue Variante, um den Zusammenhang zwischen Einheitskreis und Tangensfunktion darzustellen.

Zugriff auf alle Programme

Hier findest du 2 Lernchecks, mit denen du dein Wissen testen kannst.