AB: Flächengleichheit/Puzzles (2)
Gleicher Flächeninhalt? Im Trapez ABCD ist M der Diagonalenschnittpunkt. Sind die Dreiecke MBC und AMD flächengleich?
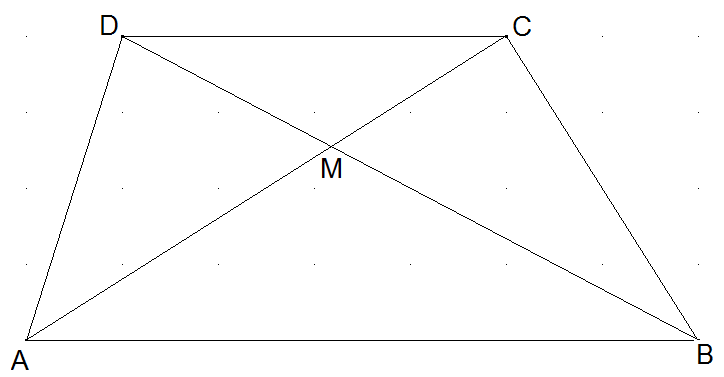
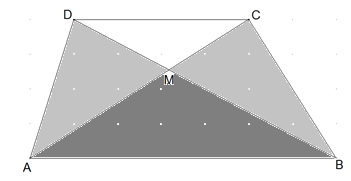
Die Flächeninhalte der Dreiecke ABC und ABD sind gleich, denn sie haben die gleiche Grundseite und Höhe. Folglich gilt FABC = FABD. Hier subtrahieren wir auf beiden Seiten die Fläche des Dreiecks ABM: FABC – FABM = FABD – FABM. Dann verbleiben links FAMD und rechts FMBC.
Teppichfliesen: Ein 17 m² großer quadratischer Raum soll mit 1m x1m-Teppichfliesen ausgelegt werden, von denen weniger als die Hälfte mit je einem geraden Schnitt zerteilt werden dürfen. Wie ist dies möglich? Tipp: Legen Sie den Grundriss des Raumes geschickt auf nebenstehendes Raster.
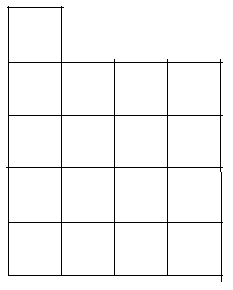
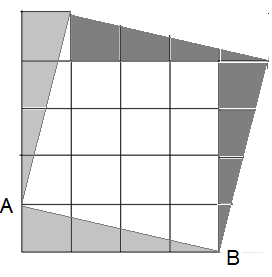
Jede Seite des quadratischen Zimmers hat das Maß √17. Nach Pythagoras ist die Länge AB gleich √17. Die hellgrauen Teile wurden abgeschnitten und als dunkelgraue eingefügt.
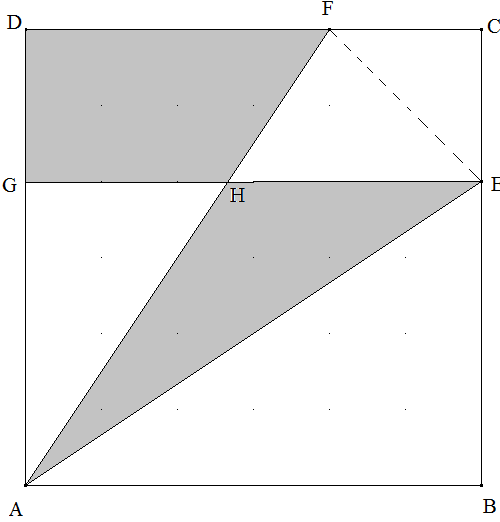
Dreieck und Trapez: Im Quadrat ABCD gilt \(\left| {\overline {EC} } \right| = \left| {\overline {CF} } \right|\) (siehe Abbildung). Die Parallele zu AB durch E schneidet AF in H und AD in G.
Zeigen Sie: Die Fläche des Dreiecks AEH ist gleich der Fläche des Trapezes GHFD. Tipp: AECF ist ein Drachenviereck.
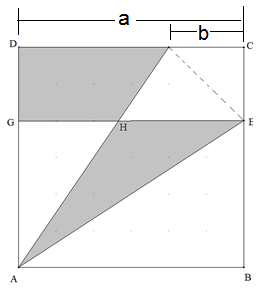
Wir nennen AB=BC=CD=CA=a und CE=CF=b. Dann sind die Diagonalenlängen im Drachenviereck AECF a·√2 und b·√2. Folglich ist der Flächeninhalt des Drachenvierecks AECF a·b und des Rechtecks GECD ebenfalls a·b. Schneidet man sowohl vom Drachenviereck AECF als auch von Rechteck GECD die Fläche des Trapezes HECF ab, bleiben jeweils die grau unterlegten Flächen übrig.
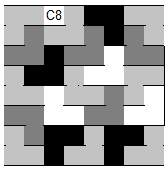
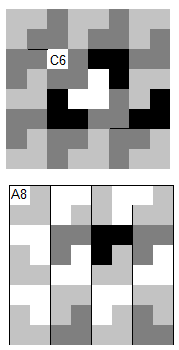
L-Trominos: Ein L-förmiger Spielstein, der drei Felder eines Schachbrettes abdeckt, soll L-Tromino heißen. Zeigen Sie: Lässt man ein beliebiges Feld eines Schachbrettes offen, kann der Rest mit L-Trominos bedeckt werden.

Wenn man die L-Trominos so anordnen kann, dass die Felder C6, C8 bzw. A8 freibleiben, lassen sich durch Drehung des Quadrates, das aus dem freien Feld und einem Tromino besteht sowie Drehung oder Spiegelung des gesamten Brettes alle Felder als freibleibend darstellen.