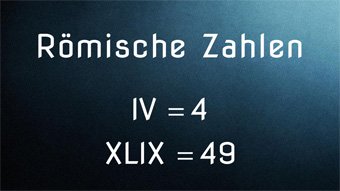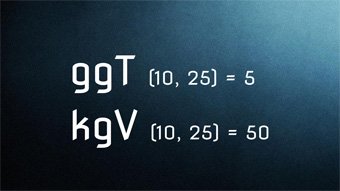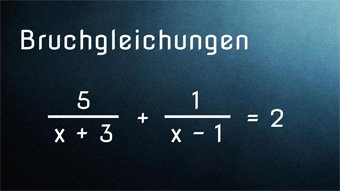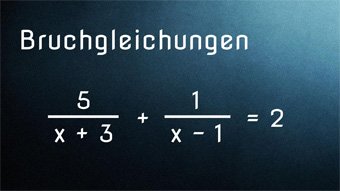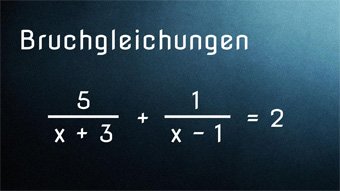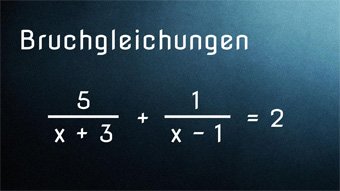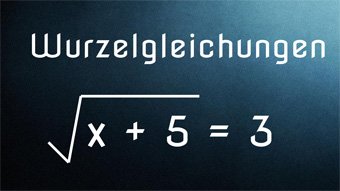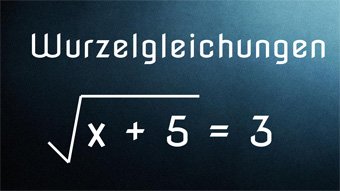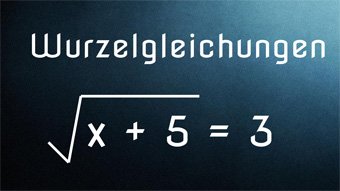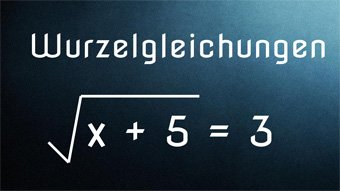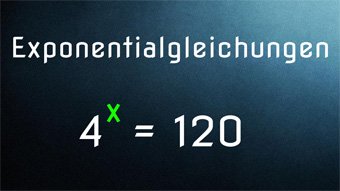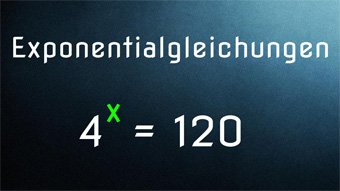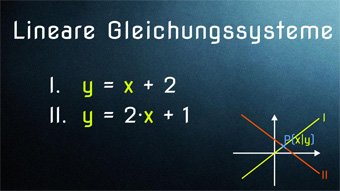Mathe-Videos
-
Intro: Matheretter kurz erklärtWas ist Matheretter? Wir erklären kurz, was das Besondere an Matheretter ist und welche Vorteile ihr habt, wenn ihr mit Matheretter lernt.Lektion öffnen
-
 11 minKlasse 5G01-1 GrundrechenartenAddition (Summand + Summand = Summe), Subtraktion (Minuend - Subtrahend = Differenz), Multiplikation (Faktor · Faktor = Produkt) und Division (Dividend : Divisor = Quotient). Zerlegen von Zahlen, Multiplikationstabelle für das Einmaleins.Lektion öffnen
11 minKlasse 5G01-1 GrundrechenartenAddition (Summand + Summand = Summe), Subtraktion (Minuend - Subtrahend = Differenz), Multiplikation (Faktor · Faktor = Produkt) und Division (Dividend : Divisor = Quotient). Zerlegen von Zahlen, Multiplikationstabelle für das Einmaleins.Lektion öffnen -
 10 minKlasse 5,6G02-1 Kommutativgesetz und AssoziativgesetzWir betrachten uns zwei wichtige Rechenregeln: Das Kommutativgesetz mit a + b = b + a sowie das Assoziativgesetz: a + b + c = (a + b) + c = a + (b + c). Beides gilt auch für die Multiplikation.Lektion öffnen
10 minKlasse 5,6G02-1 Kommutativgesetz und AssoziativgesetzWir betrachten uns zwei wichtige Rechenregeln: Das Kommutativgesetz mit a + b = b + a sowie das Assoziativgesetz: a + b + c = (a + b) + c = a + (b + c). Beides gilt auch für die Multiplikation.Lektion öffnen -
 8 minKlasse 5,6G03-1 DistributivgesetzEine der wichtigsten Rechenregeln der Mathematik ist das Distributivgesetz. Es lautet a · (b + c) = a · b + a · c. Wir können es auch um weitere Summanden erweitern, zum Beispiel: a · (b + c + d) = a · b + a · c + a·dLektion öffnen
8 minKlasse 5,6G03-1 DistributivgesetzEine der wichtigsten Rechenregeln der Mathematik ist das Distributivgesetz. Es lautet a · (b + c) = a · b + a · c. Wir können es auch um weitere Summanden erweitern, zum Beispiel: a · (b + c + d) = a · b + a · c + a·dLektion öffnen -
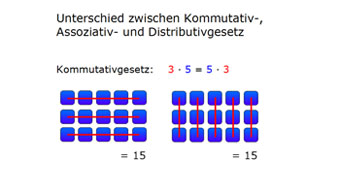
G03-2 Unterschied Kommutativ-, Assoziativ- und DistributivgesetzWir zeigen euch, was der Unterschied zwischen Kommutativgesetz, Assoziativgesetz und Distributivgesetz ist. Dabei stellen wir alle 3 Rechengesetze grafisch dar.Zugang bestellen
-
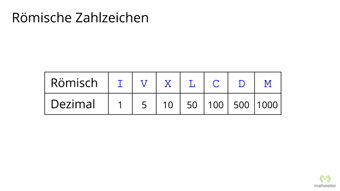
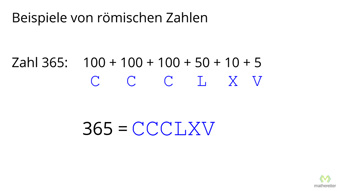
G04-1 Römische ZahlenWoher stammen die Römischen Zahlzeichen. Wie werden die Zahlen als Additionssystem dargestellt. Was ist bei der Subtraktionsregel und der Reihenfolge der Zahlzeichen zu beachten.Zugang bestellen
-
G05-1 Natürliche und Ganze ZahlenWir schauen uns die grundlenden Zahlenmengen an: Die Natürliche Zahlen (0, 1, 2, 3, ...) und die Ganzen Zahlen (..., -3, -2, -1, 0, 1, 2, 3, ...) sowie das Zeichen für Unendlich.Zugang bestellen
-
 15 minKlasse 5,6G06-1 Rechnen mit Vorzeichen - Addition und SubtraktionEinführung zum Rechnen mit Vorzeichen, Addition und Subtraktion positiver und negativer Zahlen, Herleitung der Rechenregeln, Grundlagen-Wissen Mathematik.Lektion öffnen
15 minKlasse 5,6G06-1 Rechnen mit Vorzeichen - Addition und SubtraktionEinführung zum Rechnen mit Vorzeichen, Addition und Subtraktion positiver und negativer Zahlen, Herleitung der Rechenregeln, Grundlagen-Wissen Mathematik.Lektion öffnen -
G06-2 Rechnen mit Vorzeichen - Multiplikation und DivisionErläuterung der Rechenregeln zur Multiplikation und Division mit positiven und negativen Zahlen, mehrere Beispielaufgaben zum sicheren Rechnen.Zugang bestellen
-
 11 minKlasse 8,9G07-1 Binomische Formeln - Voraussetzungen(Erweitertes) Distributivgesetz, Berechnung der Fläche von Rechteck und Quadrat, Zahl ins Quadrat (a·a = a²), 2·ab = ab + ab, Zerlegen einer Strecke in Teilstrecken.Lektion öffnen
11 minKlasse 8,9G07-1 Binomische Formeln - Voraussetzungen(Erweitertes) Distributivgesetz, Berechnung der Fläche von Rechteck und Quadrat, Zahl ins Quadrat (a·a = a²), 2·ab = ab + ab, Zerlegen einer Strecke in Teilstrecken.Lektion öffnen -
G07-2 Binomische Formeln - Erste Binomische FormelHerleitung der 1. Binomischen Formel, Grafischer Nachweis der 1. Binomischen Formel über Flächen.Zugang bestellen
-
G07-3 Binomische Formeln - Zweite Binomische FormelHerleitung der 2. Binomischen Formel, Grafischer Nachweis, Anwendung bei der Aufgabe (3xy-5)²Zugang bestellen
-
G07-4 Binomische Formeln - Dritte Binomische FormelHerleitung der 3. Binomischen Formel, Faktorisieren, Schnelleres Kopfrechnen mit Binomischen Formeln.Zugang bestellen
-
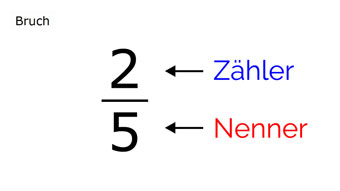
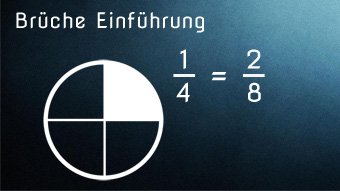 8 minKlasse 6,7G08-1 Brüche - Einführung, Erweitern und KürzenEine einfache Einführung: Zähler und Nenner, Erweitern und Kürzen von Brüchen, Zusammenhang zwischen Division und Bruch.Lektion öffnen
8 minKlasse 6,7G08-1 Brüche - Einführung, Erweitern und KürzenEine einfache Einführung: Zähler und Nenner, Erweitern und Kürzen von Brüchen, Zusammenhang zwischen Division und Bruch.Lektion öffnen -
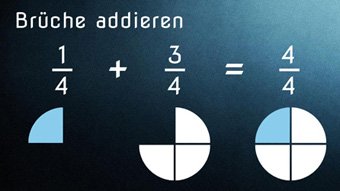
G08-2 Brüche - Addition + SubtraktionAddition und Subtraktion von Brüchen mit gleichen und verschiedenen Nennern, Brüche gleichnamig machen (gemeinsamen Nenner bilden).Zugang bestellen
-
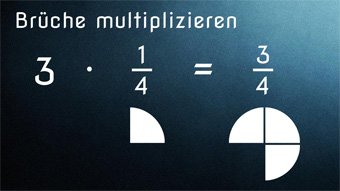
G08-3 Brüche - MultiplikationMultiplikation von Zahl mal Bruch sowie Bruch mal Bruch. Umwandlung einer Zahl in einen Bruch, Herleitung der Multiplikationsregeln für Brüche, Veranschaulichung der einzelnen Rechenschritte.Zugang bestellen
-
G08-4 Brüche - DivisionDivision von Brüchen inklusive Herleitung der Regeln, Kehrwert/Reziproke, Doppelbruch, Zusammenfassung Bruchrechenregeln. Am Videobeginn: Rechentrick Diagonalkürzen bei Multiplikation.Zugang bestellen
-
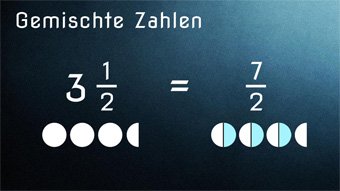
G08-5 Brüche - Brucharten + Gemischte ZahlenStammbruch, echter und unechter Bruch, Scheinbruch, Dezimalbruch (Dezimalzahl), Rechnen mit Gemischten Zahlen, Umwandlung Bruch ↔ Gemischte Zahl, Zahlenmenge: Rationale Zahlen, Vorzeichen bei Zähler und Nenner.Zugang bestellen
-
G08-61 Einführung Brüche, Zähler und NennerEinführung zu den Brüchen. Was ist ein Bruch? Bestandteile Zähler und Nenner.Zugang bestellen
-
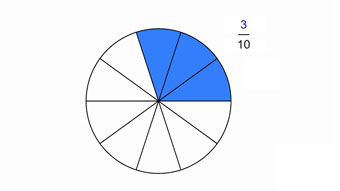
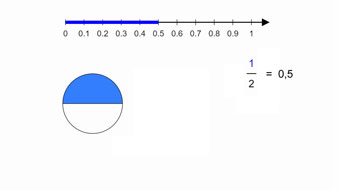
G08-62 Brüche am KreisEchte Brüche wie 1/2 lassen sich grafisch am Kreis darstellen.Zugang bestellen
-
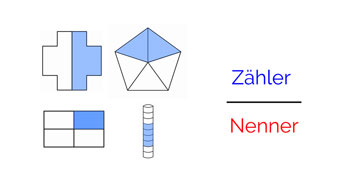
G08-63 Bruchzahlen und AnteileBrüche lassen sich als Anteile von einem Ganzen verstehen. Das Ganze teilt man in mehrere gleichgroße Teile.Lektion öffnen
-
G08-64 Brüche am ZahlenstrahlBrüche lassen sich an einem Zahlenstrahl abtragen. Wir setzen einen Strich dort, wo der Dezimalwert des Bruches ist.Zugang bestellen
-
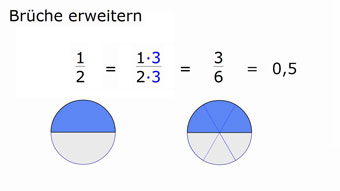
G08-65 Brüche erweiternBeim Erweitern von Brüchen werden Nenner und Zähler mit der gleichen Zahl multipliziert. Beispiele.Zugang bestellen
-
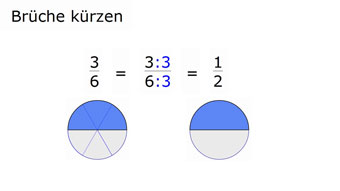
G08-66 Brüche kürzenBeim Kürzen von Brüchen werden Nenner und Zähler werden mit der gleichen Zahl dividiert. Primfaktorzerlegung zum vollständigen Kürzen.Zugang bestellen
-
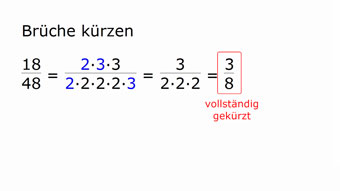
G08-67 Brüche vollständig kürzenVollständig gekürzt bedeutet, dass ein Bruch nicht mehr kürzbar ist.Zugang bestellen
-
G08-68 Brüche sinnvoll erweiternWir können uns Rechenaufwand ersparen, indem wir Brüche sinnvoll erweitern.Zugang bestellen
-
G08-69 Gleichnamige Brüche vergleichenWir vergleichen gleichnamige Brüche und ordnen sie der Größe nach.Zugang bestellen
-
G08-70 Ungleichnamige Brüche vergleichenWir vergleichen ungleichnamige Brüche miteinander und ordnen sie der Größe nach.Zugang bestellen
-
G08-71 Gemischte Zahlen und BrücheEinführung gemischte Zahlen. Gemischte Zahl in Bruch umwandeln. Bruch in gemischte Zahl umwandeln.Zugang bestellen
-
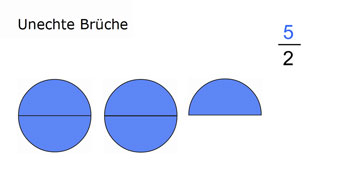
G08-73 Unechte BrücheBei unechten Brüchen ist der Zähler größer als der Nenner. Beispiel: 5/2. Wir vergleichen und sortieren unechte Brüche.Lektion öffnen
-
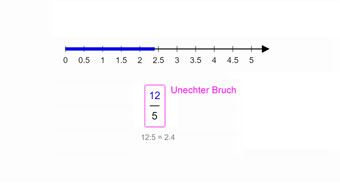
G08-74 Unechte Brüche am ZahlenstrahlUnechte Brüche haben einen Dezimalwert von größer 1. Man kann sie auf dem Zahlenstrahl abtragen.Zugang bestellen
-
G08-75 Größen mit Brüchen angebenWir geben Größen aus dem Alltag als Brüche und als Dezimalzahlen an.Zugang bestellen
-
G08-76 Einheiten mit Brüchen umrechnenWir rechnen Einheiten mit Hilfe von Brüchen um. Zum Beispiel Meter in Millimeter oder Kilogramm zu Gramm.Zugang bestellen
-
G09-1 Rechnen mit Kommazahlen - Einführung und RegelnEinführung zum Rechnen mit Kommazahlen, Bestandteile der Kommazahl, Regeln für die Addition, Subtraktion, Multiplikation und Division von Kommazahlen.Zugang bestellen
-
G09-2 Rechnen mit Kommazahlen - Rechenregeln + DezimalbrücheAdditionsregel und Multiplikationsregel erläutert, Dezimalbrüche (Dezimalzahlen), Umwandlung zwischen Kommazahl ↔ Bruch, Kommazahlen als Brüche rechnen.Zugang bestellen
-
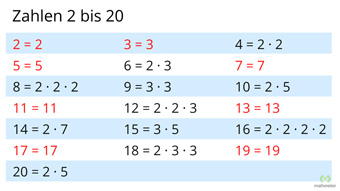
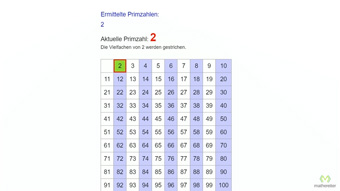
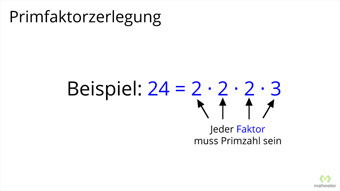
G10-1 Primzahlen und PrimfaktorzerlegungPrimzahlen (Natürliche Zahlen, die nur Teiler 1 und sich selbst haben) und die Primfaktorzerlegung (Darstellung einer Zahl als Multiplikation von Primzahlen). Methode zum Finden von Primzahlen.Zugang bestellen
-
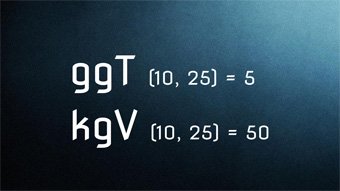 10 minKlasse 6,7G11-1 ggT und kgV - Größter gemeinsamer TeilerWas ist der größte gemeinsame Teiler zweier Zahlen, Bedeutung und Anwendung.Lektion öffnen
10 minKlasse 6,7G11-1 ggT und kgV - Größter gemeinsamer TeilerWas ist der größte gemeinsame Teiler zweier Zahlen, Bedeutung und Anwendung.Lektion öffnen -
G11-2 ggT und kgV - Kleinstes gemeinsames VielfachesWas ist das kleinste gemeinsame Vielfache, ausführliche Erklärung und Anwendung bei den Brüchen.Zugang bestellen
-
 10 minKlasse 7G12-1 Terme und Gleichungen - EinführungWas ist ein Term, Umformen von Termen (Termumformung), Gleichungen umstellen (sogenannte Äquivalenzumformung).Lektion öffnen
10 minKlasse 7G12-1 Terme und Gleichungen - EinführungWas ist ein Term, Umformen von Termen (Termumformung), Gleichungen umstellen (sogenannte Äquivalenzumformung).Lektion öffnen -
G12-2 Terme und Gleichungen - ÄquivalenzumformungHinführung zur Unbekannten x in einer Gleichung, Lösung von 2 Beispielaufgaben mittels Aufstellen von Gleichungen, Lösungsmöglichkeiten für x (ein, kein, unendlich viele Ergebnisse).Zugang bestellen
-
 14 minKlasse 8G13-1 Termumformung - AusmultiplizierenWas sind Term und Gleichung, Gleichungen lösen, Kurzschreibweise 2x. Ausmultiplizieren als Anwendung des Distributivgesetzes. Ausmultiplizieren mit Variablen in Klammern. Lösen der Gleichung: 2·(3x+5) = 22 sowie 5·(2x-3) = (3x-4)·4. Wie muss man zwei Klammern miteinander multiplizieren.Lektion öffnen
14 minKlasse 8G13-1 Termumformung - AusmultiplizierenWas sind Term und Gleichung, Gleichungen lösen, Kurzschreibweise 2x. Ausmultiplizieren als Anwendung des Distributivgesetzes. Ausmultiplizieren mit Variablen in Klammern. Lösen der Gleichung: 2·(3x+5) = 22 sowie 5·(2x-3) = (3x-4)·4. Wie muss man zwei Klammern miteinander multiplizieren.Lektion öffnen -
G13-2 Termumformung - AusklammernAusklammern und das Distributivgesetz. Ausklammern beim Term 24+10x. Wie finden wir die auszuklammernde Zahl (Primfaktorzerlegung/ggT). Lösen der Gleichung: x²+30x=0. Ausklammern bei Termen: 9a+3, 5xy+10xz und 36c²d+3cd+48cd².Zugang bestellen
-
G13-3 Termumformung - Binomische FormelnLösen der Gleichung x²-4x+4=0 mit der Binomischen Formel. Vereinfachen und lösen der Bruchterm-Gleichung: (x²-4)/(x+2)=0. Vereinfachen von Termen: (ab+0,5cd)², (x-1)(x+1)(x+3), (5yx³-5y³x)/(x-y), 25a²b²-225a². Unterschied zwischen Term- und Äquivalenzumformung.Zugang bestellen
-
G14-1 UngleichungenWie lassen sich Ungleichungen lösen. Welche Zeichen und Regeln benötigen wir. Umstellen von Ungleichungen und umformen von Termen. Größer und kleiner, größergleich und kleinergleich.Zugang bestellen
-
 11 minKlasse 6,7G15-1 Proportionalität und DreisatzBedeutung der Proportionalität: Steigt ein Wert so steigt auch ein anderer, sinkt ein Wert so sinkt auch ein anderer. Dreisatz: Unbekannten Wert aus 3 gegebenen Werten ermitteln. Beispielaufgaben.Lektion öffnen
11 minKlasse 6,7G15-1 Proportionalität und DreisatzBedeutung der Proportionalität: Steigt ein Wert so steigt auch ein anderer, sinkt ein Wert so sinkt auch ein anderer. Dreisatz: Unbekannten Wert aus 3 gegebenen Werten ermitteln. Beispielaufgaben.Lektion öffnen -
G16-1 Antiproportionalität (Indirekte Proportionalität)Antiproportional bzw. indirekt proportional: Erhöht sich ein Wert so verringert sich ein anderer, verringert sich ein Wert, so erhöht sich ein anderer. Lösung über Antiproportionalitätsfaktor und Dreisatz.Zugang bestellen
-
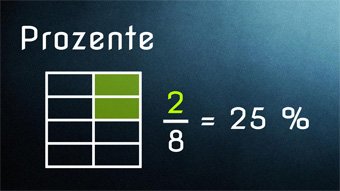
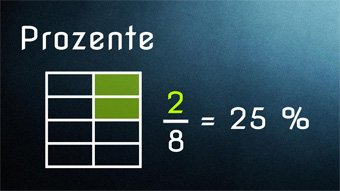
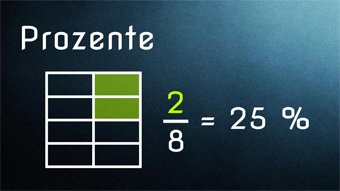
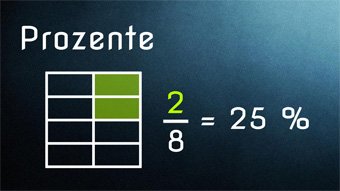 11 minKlasse 6,7G17-1 Prozentrechnung - Einführung Prozent %Was ist Prozent, was bedeutet das Prozentzeichen, was sind Anteile, Zusammenhang zwischen Bruch, Prozent und Zahl.Lektion öffnen
11 minKlasse 6,7G17-1 Prozentrechnung - Einführung Prozent %Was ist Prozent, was bedeutet das Prozentzeichen, was sind Anteile, Zusammenhang zwischen Bruch, Prozent und Zahl.Lektion öffnen -
G17-2 Prozentrechnung - Grundwert + ProzentwertÜber den Dreisatz zu den Formeln für Grundwert (Gesamtmenge) und Prozentwert (Anteil).Zugang bestellen
-
G17-3 Prozentrechnung - ProzentsatzHerleitung der Formel für den Prozentsatz, Aufgaben und Lösungen zur Prozentrechnung, Rechentricks für schnelleres Prozentrechnen.Zugang bestellen
-
G17-4 Prozentrechnung - Häufige FehlerquellenHäufige Fehlerquellen, Prozentsätze über 100 %, bequeme Prozentsätze, Lehrbücher mit Formeln ·100, Rechnen mit Promille.Zugang bestellen
-
 10 minKlasse 6,7G18-1 Zinsrechnung - Einführung Kapital, Zinsen, ZinssatzWas sind Kapital, Zinsen und Zinssatz und wie rechnen wir damit. Berechnung anhand von Beispielaufgaben.Lektion öffnen
10 minKlasse 6,7G18-1 Zinsrechnung - Einführung Kapital, Zinsen, ZinssatzWas sind Kapital, Zinsen und Zinssatz und wie rechnen wir damit. Berechnung anhand von Beispielaufgaben.Lektion öffnen -
G18-2 Zinsrechnung - Kapital ermittelnBeispielaufgabe: Kapital errechnen aus Zinsen und Zinssatz.Zugang bestellen
-
G18-3 Zinsrechnung - Zeitgenaue ZinsrechnungWie berechnet man tag- und monatsgenaue Zinsen, Zins-Formeln, Beispielaufgaben, Zeitraum der Geldanlage aus gegebenen Werten ermitteln, Zählweise für Tage.Zugang bestellen
-
 11 minKlasse 7,8,9G19-1 Potenzen - EinführungWas ist eine Potenz, Bestandteile Basis, Exponent und Potenzwert. Herleitung der grundlegenden Potenzgesetze.Lektion öffnen
11 minKlasse 7,8,9G19-1 Potenzen - EinführungWas ist eine Potenz, Bestandteile Basis, Exponent und Potenzwert. Herleitung der grundlegenden Potenzgesetze.Lektion öffnen -
G19-2 Potenzen - PotenzgesetzePotenzregel bei Division mit unterschiedlicher Basis, Herleitung der Regel: x hoch 0 = 1, Rechenregeln bei x hoch negativem Exponenten, positives bzw. negatives Ergebnis bei geradem oder ungeradem Exponenten, Lösung von Beispielaufgaben.Zugang bestellen
-
 11 minKlasse 9,10G20-1 Zinseszins - EinführungVerzinsung von Kapital und Zinsen über mehrere Jahre, Anwendung der Zinseszinsformel zur direkten Berechnung des Endkapitals aus Startkapital, Zinssatz und Anzahl an Jahren.Lektion öffnen
11 minKlasse 9,10G20-1 Zinseszins - EinführungVerzinsung von Kapital und Zinsen über mehrere Jahre, Anwendung der Zinseszinsformel zur direkten Berechnung des Endkapitals aus Startkapital, Zinssatz und Anzahl an Jahren.Lektion öffnen -
G20-2 Zinseszins - ZinseszinsformelAusführliche Herleitung der Zinseszinsformel unter Nutzung der Prozent- und Potenzgesetze, Anwendung bei Beispielaufgabe mit nachvollziehbarem Lösungsweg.Zugang bestellen
-
 11 minKlasse 9G21-1 Wurzeln - EinführungWurzel als Umkehrung der Potenz. Begriffe: Wurzelexponent, Radikand und Wurzelwert, Wurzelziehen (Radizieren), Ursprung des Wurzelzeichens √, Quadratwurzel, Umwandlung einer Wurzel zu einer Potenz, Wurzelgesetz für Multiplikation.Lektion öffnen
11 minKlasse 9G21-1 Wurzeln - EinführungWurzel als Umkehrung der Potenz. Begriffe: Wurzelexponent, Radikand und Wurzelwert, Wurzelziehen (Radizieren), Ursprung des Wurzelzeichens √, Quadratwurzel, Umwandlung einer Wurzel zu einer Potenz, Wurzelgesetz für Multiplikation.Lektion öffnen -
G21-2 Wurzeln - WurzelgesetzeDivision von Wurzeln, Wurzel aus Wurzel (Doppelwurzel), Teilweises Wurzelziehen, Wurzel aus Null, Nullte Wurzel, Rechnen mit negativem Wurzelexponenten, Zusammenfassung der wichtigsten Wurzelrechenregeln.Zugang bestellen
-
G21-3 Wurzeln - Vertieftes WissenWurzeln aus negativen Zahlen, n-te Wurzel aus Eins, Widerspruch beim Wurzel-Potenz-Umwandeln, Beispielaufgaben für Anwendung der Wurzel, Plusminus-Wurzel.Zugang bestellen
-
 10 minKlasse 9G22-1 Irrationale Zahlen, Reelle ZahlenWas sind Irrationale Zahlen (nicht als Bruch a/b darstellbar). Wiederholung der bekannten Zahlenmengen. Nachweis, dass Wurzel aus Zwei nicht als Bruch darstellbar ist. Hinleitung zu den Irrationalen Zahlen und Reelle Zahlen. Reelle Zahlen bestehen aus Rationalen und Irrationalen Zahlen.Lektion öffnen
10 minKlasse 9G22-1 Irrationale Zahlen, Reelle ZahlenWas sind Irrationale Zahlen (nicht als Bruch a/b darstellbar). Wiederholung der bekannten Zahlenmengen. Nachweis, dass Wurzel aus Zwei nicht als Bruch darstellbar ist. Hinleitung zu den Irrationalen Zahlen und Reelle Zahlen. Reelle Zahlen bestehen aus Rationalen und Irrationalen Zahlen.Lektion öffnen -
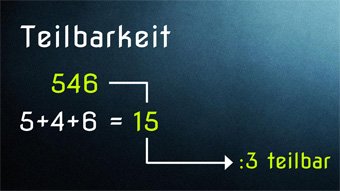
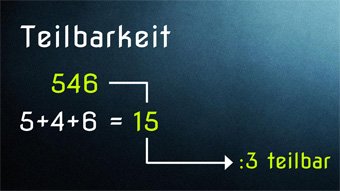
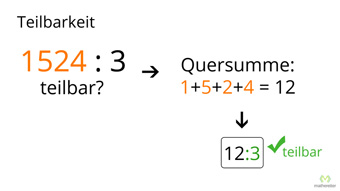
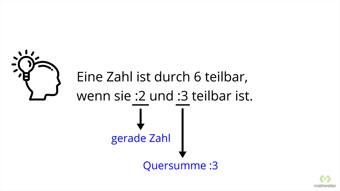
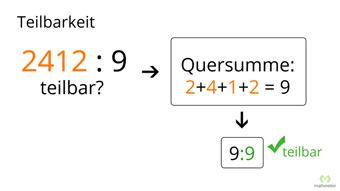
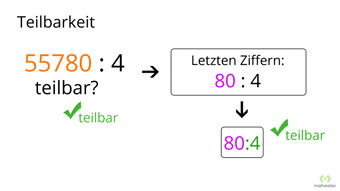
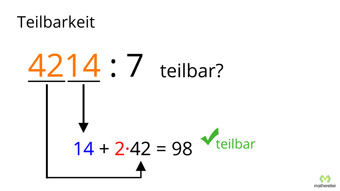
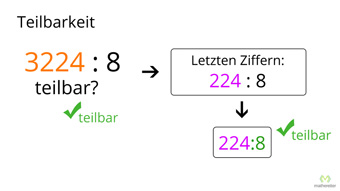
G23-1 Teilbarkeit - Regeln für Division durch 0, 1, 2, 3, 4Wieso ist die Division durch Null nicht definiert. Was ist eine Quersumme und wozu braucht man sie. Herleitung der Teilbarkeitsregeln von Eins bis Vier.Zugang bestellen
-
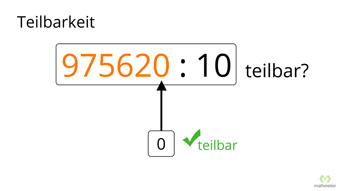
G23-2 Teilbarkeit - Regeln für Division durch 5 bis 10Teilbarkeitsregeln für Fünf, Sechs, Sieben, Acht, Neun, Zehn, Anwendung bei den Brüchen, Zusammenfassung aller Teilbarkeitsregeln.Zugang bestellen
-
 10 minKlasse 10G24-1 Einführung Logarithmus - Was ist der LogarithmusEinführung zum Logarithmus, Schreibweise Logarithmus, Zusammenhang Logarithmus und Potenz, Begriffe Basis und Numerus, 1. und 2. Logarithmusgesetz (inklusive Herleitung).Lektion öffnen
10 minKlasse 10G24-1 Einführung Logarithmus - Was ist der LogarithmusEinführung zum Logarithmus, Schreibweise Logarithmus, Zusammenhang Logarithmus und Potenz, Begriffe Basis und Numerus, 1. und 2. Logarithmusgesetz (inklusive Herleitung).Lektion öffnen -
G24-2 Logarithmus - Logarithmusregeln3., 4. und 5. Logarithmusregel inklusive Herleitung, Logarithmusarten: Dekadischer (lg) und natürlicher Logarithmus (ln) sowie Logarithmus Dualis (ld), Berechnung von beliebigen Logarithmen mit dem 10er Logarithmus.Zugang bestellen
-
G24-3 Logarithmus - Anwendung bei SachaufgabenLogarithmieren mit dem Taschenrechner, weitere wichtige Regeln, Anwendung des Logarithmus bei zwei Sachaufgaben (mit ausführlicher Lösung).Zugang bestellen
-
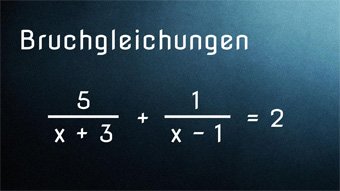 12 minKlasse 8,9,10G25-1 Bruchgleichungen - Einführung und VoraussetzungenWas ist eine Bruchgleichung. Wiederholung des Wissens zu den Brüchen und zum Umformen von Gleichungen. Lösen der Bruchgleichung 2/x = 0,5 durch Umformen der Gleichung. Lösen von 2/(x+3) = 5 mit Probe.Lektion öffnen
12 minKlasse 8,9,10G25-1 Bruchgleichungen - Einführung und VoraussetzungenWas ist eine Bruchgleichung. Wiederholung des Wissens zu den Brüchen und zum Umformen von Gleichungen. Lösen der Bruchgleichung 2/x = 0,5 durch Umformen der Gleichung. Lösen von 2/(x+3) = 5 mit Probe.Lektion öffnen -
G25-2 Bruchgleichungen - Lösung durch Umformen und ErweiternLösung durch Umformen von Gleichungen und Erweitern der Brüche (Nenner gleichnamig machen): Wir berechnen 1/(x+8) = 5/x und 2/x + 1/2x = 5. Auch machen wir jeweils die Probe. Zusätzlich lösen wir den Term 10x²+5x=0. Einführung und Bedeutung der Definitionsmenge.Zugang bestellen
-
G25-3 Bruchgleichungen - Lösen mit Hilfe der Binomischen FormelDefinitionsmenge bestimmen bei 2/(x+2) und 5/(x-2). Lösen der Bruchgleichung 2/(x+2) + 5/(x-2) = 20/(x²-4) mit Hilfe der Binomischen Formel (gleichnamige Nenner). Leere Lösungsmenge. Lösen der Bruchgleichung 2/(x+2) + 1/(x-2) = 1/(x²-4). Probe.Zugang bestellen
-
G25-4 Bruchgleichungen - Lösen mit Ausklammern und ErweiternLösen der Gleichung (x-1)/(4x+2) + 9/4 = 3/(2x+1) durch Bilden eines gemeinsamen Nenners mittels Ausklammern und Erweitern. Lösen von 3/a - 2/3a + 1/6a = 5 sowie 3/(n-1) = 4/(n-2). Bestimmen der Definitionsmenge und Überprüfen des Ergebnisses.Zugang bestellen
-
G25-5 Bruchgleichungen - Lösen mit Normalform und p-q-FormelLösen von (x+1)/x + (x+2)/x = x mittels Umformung in die Normalform und Anwenden der p-q-Formel. Zusammenfassung des Wissens. Abschließende Übungsaufgaben mit Lösung: (1+b)/2b = 5/4b + 1/4 und 5/2y + 4/3y = 7/2 und 3/(z-3) - 2/(z-3) = 4/(z²-6z+9)Zugang bestellen
-
G26-1 Lineare Gleichungen - EinführungEinführung zu den linearen Gleichungen. Lösen von linearen Gleichungen mittels Äquivalenzumformung und per Deutung als Funktionen. Lösungsmengen.Zugang bestellen
-
G26-2 Unterschied zwischen Gleichung und FunktionUnterschied zwischen Gleichung und Funktion. Speziell quadratische Gleichungen und quadratische Funktionen.Zugang bestellen
-
 11 minKlasse 9G26-3 Quadratische Gleichungen - EinführungWas sind Quadratische Gleichungen, Allgemeinform und Normalform, Quadratisches Glied, Lineares Glied, Absolutes Glied, Koeffizienten, Lösen einer quadratischen Gleichung mit Hilfe der p-q-Formel, Lösen der Gleichung mittels Deutung als Funktion.Lektion öffnen
11 minKlasse 9G26-3 Quadratische Gleichungen - EinführungWas sind Quadratische Gleichungen, Allgemeinform und Normalform, Quadratisches Glied, Lineares Glied, Absolutes Glied, Koeffizienten, Lösen einer quadratischen Gleichung mit Hilfe der p-q-Formel, Lösen der Gleichung mittels Deutung als Funktion.Lektion öffnen -
G26-4 Quadratische Gleichungen - Herleitung p-q-FormelHerleitung der p-q-Formel, weitere Lösungsverfahren für quadratische Gleichungen (Wurzeln, Ausklammern, Linearfaktoren), Grafisches Lösen von quadratischen Gleichungen.Zugang bestellen
-
G26-5 Quadratische Gleichungen - abc-FormelHerleitung der abc-Formel (große Lösungsformel bzw. Mitternachtsformel), Lösen Quadratischer Gleichungen mit abc-Formel, Zusammenfassung des neuen Wissens.Zugang bestellen
-
 11 minKlasse 10,11G27-1 Kubische Gleichungen - EinführungBedeutung "kubisch". Allgemeinform und Normalform der kubischen Gleichung (Gleichungen 3. Grades), Auflistung von Lösungsverfahren, Anzahl von Lösungen (bzw. Nullstellen bei Deutung als Funktion), was ist ein Polynom und ein Monom, Einleitung zur Division von Polynomen.Lektion öffnen
11 minKlasse 10,11G27-1 Kubische Gleichungen - EinführungBedeutung "kubisch". Allgemeinform und Normalform der kubischen Gleichung (Gleichungen 3. Grades), Auflistung von Lösungsverfahren, Anzahl von Lösungen (bzw. Nullstellen bei Deutung als Funktion), was ist ein Polynom und ein Monom, Einleitung zur Division von Polynomen.Lektion öffnen -
G27-2 Polynomdivision - Anwendung des VerfahrensLösungsverfahren Polynomdivision, das den Grad des Polynoms vermindert, Wiederholung schriftliche Division, Einführung zum Verfahren der Polynomdivision am Beispiel (x²-4x-5):(x-5)Zugang bestellen
-
G27-3 Polynomdivision - Erklärung des VerfahrensWir erklären, warum die Polynomdivision funktioniert bzw. wie Polynome dividiert werden. Darstellung der Division als Bruch, Umformung mittels Erweitern des Zählers sowie Ergänzung des Zählerterms und anschließendes Kürzen.Zugang bestellen
-
G27-4 Kubische Gleichungen - LösungsverfahrenLösung von (x³+6x²+11x+6):(x+1) mit Polynomdivision und p-q-Formel. Polynom in Linearfaktorform, Deutung als Funktionen. Lösen über Ausklammern.Zugang bestellen
-
G27-5 Kubische Gleichungen - LösungsverfahrenLösen mit Wurzel bei reinkubischen Gleichungen. Erklärung der Polynomdivision mit Rest. Lösungsmenge Reelle und Komplexe Zahlen.Zugang bestellen
-
G27-6 Gleichung 3. Grades lösen mit Polynomdivision und pq-FormelAnwendung des neuen Wissens: Zuerst raten wir systematisch die erste Lösung der Gleichung x³-6x²+11x-6=0, danach wenden wir die Polynomdivision an und erhalten einen Term zweiten Grades, der null gesetzt wird und sich mit der pq-Formel lösen lässt.Zugang bestellen
-
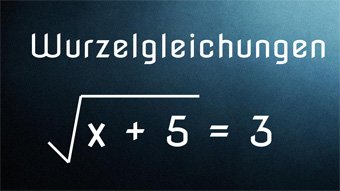 12 minKlasse 9,10G28-1 Wurzelgleichungen - Einführung, DefinitionsmengeWiederholung der wichtigsten Regeln zu den Wurzeln. Einführung Wurzelgleichung und Lösung von 3 = √(x+5) mittels Quadrieren. Definitionsmenge festlegen, da Radikand nicht negativ werden darf. Pflichtprobe bei Wurzeln. Lösung der Wurzelgleichungen √(3·x) = √(14+x) und √(15-2·x) + 1 = 3,5 mit Proben.Lektion öffnen
12 minKlasse 9,10G28-1 Wurzelgleichungen - Einführung, DefinitionsmengeWiederholung der wichtigsten Regeln zu den Wurzeln. Einführung Wurzelgleichung und Lösung von 3 = √(x+5) mittels Quadrieren. Definitionsmenge festlegen, da Radikand nicht negativ werden darf. Pflichtprobe bei Wurzeln. Lösung der Wurzelgleichungen √(3·x) = √(14+x) und √(15-2·x) + 1 = 3,5 mit Proben.Lektion öffnen -
G28-2 Wurzelgleichungen - Lösen mit p-q-Formel, Wurzel-AmbiguitätLösung der Wurzelgleichung 1+x=√(4-x) mit Hilfe der p-q-Formel. Ambiguität (Zweideutigkeit) der Wurzel und Scheinlösungen. Lösungsmenge bei Wurzelgleichungen. Quadratwurzel führt immer zu postivem Ergebnis.Zugang bestellen
-
G28-3 Wurzelgleichungen - Lösungsschritte, Lösen mit GraphenLösungsschritte für Wurzelgleichungen. Lösung der Gleichung 4·√(x)=100 sowie 3·√(x-16)=√(20+x) und √(3+x)=x+5. Wurzelgleichungen lösen über Deutung als Funktionsgraphen und Schnittpunkt finden. Lösung von √(3+x)=x über Funktionsgraphen.Zugang bestellen
-
G28-4 Wurzelgleichungen - Verschachtelte Wurzeln, 4. WurzelLösung einer Wurzelgleichung mit verschachtelter Wurzel: √(-x + √(-x+5)) = 4 mit p-q-Formel. Lösung einer Gleichung mit 4. Wurzel: √(3x+3)=⁴√(-9x) mit Potenzierung. Wurzelgleichung mit 2. und 3. Wurzel durch Umwandlung in Potenzen.Zugang bestellen
-
G28-5 Wurzelgleichungen - Wurzeln selbst berechnenWurzeln mittels Intervallschachtelung berechnen, Methode 1: Annäherung an die Grenze über weitere Nachkommastellen, Methode 2: Annäherung über den Mittelwert aus den Grenzen. Heron-Verfahren zur Bestimmung des Wurzelwertes inklusive geometrischer Deutung.Zugang bestellen
-
G29-1 Biquadratische Gleichungen - SubstitutionÜbersicht zu Gleichungen 1. bis 3. Grades. Was sind biquadratische Gleichungen und wie können wir diese mit Hilfe der Substitution (Ersetzung) berechnen. Lösung am Beispiel: -0,5·x⁴ + 4·x² - 3,5 = 0.Zugang bestellen
-
G29-2 Biquadratische Gleichungen - Quartische GleichungenWir lösen reduzierte Quartische Gleichungen (4. Grad) mit Wurzelziehen, Ausklammern und Satz vom Nullprodukt. Lösung als Nullstellen von Funktionsgraphen. Zusammenfassung der Lösungsverfahren für die Gleichungstypen. Lösen einer Gleichung 6. Grades per Substitution.Zugang bestellen
-
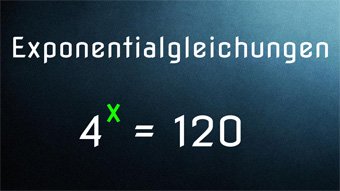 9 minKlasse 9,10G30-1 Exponentialgleichungen - Einführung: Lösen mit LogarithmusWas sind Exponentialgleichungen. Wiederholung Potenz und wichtigste Logarithmusregeln (Logarithmus berechnen über log10, Exponent mit Logarithmus herausziehen). Exponent mit log im Taschenrechner ermitteln. Lösen der Exponentialgleichung: 4^x = 120Lektion öffnen
9 minKlasse 9,10G30-1 Exponentialgleichungen - Einführung: Lösen mit LogarithmusWas sind Exponentialgleichungen. Wiederholung Potenz und wichtigste Logarithmusregeln (Logarithmus berechnen über log10, Exponent mit Logarithmus herausziehen). Exponent mit log im Taschenrechner ermitteln. Lösen der Exponentialgleichung: 4^x = 120Lektion öffnen -
G30-2 Exponentialgleichungen - Lösen mit lg und PotenzgesetzenLösung der Exponentialgleichung 7^(x+2) = 451, Lösung für 3^x + 3^(x-2) = 270 mit Potenzgesetz und lg, Lösung für 2^3x = 3^4x : 3^x · 54, gleiche Basis herstellen und Logarithmus anwendenZugang bestellen
-
G30-3 Exponentialgleichungen - Lösen mit SubstitutionLösung der Exponentialgleichung 16^x = 4^x · 2, Gleichung als Funktionen deuten, Lösung für 5^2x + 5^x - 30 = 0, Substituieren und mit p-q-Formel auflösen, Lösung für 2^x = 5^x-2 mit lg und Ausmultiplizieren, Hinweis zu 3^x + 4^x = 5^x (numerisches Lösungsverfahren)Zugang bestellen
-
 10 minKlasse 9,10G31-1 Die 10 häufigsten Mathefehler - und wie ihr sie vermeidet!In diesem Video stellen wir die häufigsten Mathefehler von Schülern vor. Diese Fehler kosten meist wertvolle Punkte und führen dazu, dass die Noten von Schülern schlechter ausfallen.Lektion öffnen
10 minKlasse 9,10G31-1 Die 10 häufigsten Mathefehler - und wie ihr sie vermeidet!In diesem Video stellen wir die häufigsten Mathefehler von Schülern vor. Diese Fehler kosten meist wertvolle Punkte und führen dazu, dass die Noten von Schülern schlechter ausfallen.Lektion öffnen -
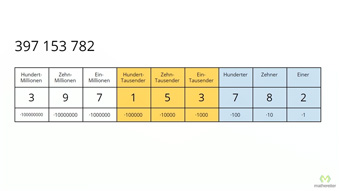
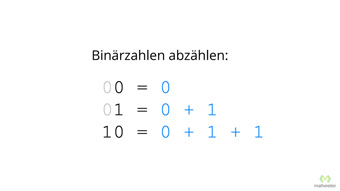
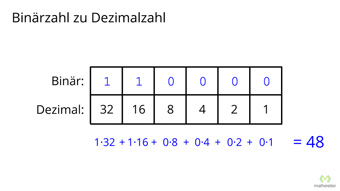
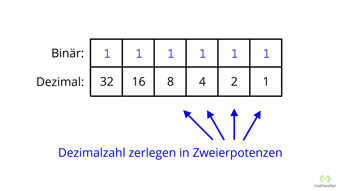
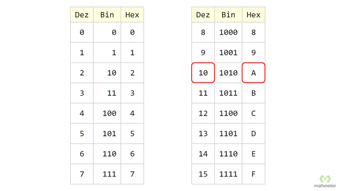
 15 minKlasse 9,10G32-1 Einführung der Binärzahlen mit Hilfe der DezimalzahlenWas ist eine Binärzahl, was ist eine Dezimalzahl. Begriffe Binärsystem, Dualsystem, Zweiersystem. Zerlegen einer Dezimalzahl in Zehnerpotenzen, Stellenwertsystem erklärt, Zweierpotenzen beim Binärsystem. Beispiel einer Umrechnung von Binär- zu Dezimalzahl.Lektion öffnen
15 minKlasse 9,10G32-1 Einführung der Binärzahlen mit Hilfe der DezimalzahlenWas ist eine Binärzahl, was ist eine Dezimalzahl. Begriffe Binärsystem, Dualsystem, Zweiersystem. Zerlegen einer Dezimalzahl in Zehnerpotenzen, Stellenwertsystem erklärt, Zweierpotenzen beim Binärsystem. Beispiel einer Umrechnung von Binär- zu Dezimalzahl.Lektion öffnen -
G32-2 Dezimalzahlen in Binärzahlen umwandelnUmwandeln der Dezimalzahl 178 in die Binärzahl 10110010. Zerlegung der Dezimalzahl in eine Summe von Zweierpotenzen, Rechenweg erklärt. Alternative Rechenmethode über das Divisionsverfahren (Restverfahren).Zugang bestellen
-
G32-3 Binärzahlen addieren und subtrahierenAddition von Binärzahlen wie bei den Dezimalzahlen, einzelnen Stellen addieren mit Übertrag. Andere Rechenmethode bei Subtraktion: Wir splitten den Minuenden solange auf, bis der Subtrahend ziffernweise von ihm abgezogen werden kann. Nach dem Abzug addieren wir alle Stellen zusammen.Zugang bestellen
-
G32-4 Binärzahlen multiplizieren und dividierenSchriftliche Multiplizieren von Binärzahlen wie bei Dezimalzahlen, wir multiplizieren die einzelnen Stellen mit dem ersten Faktor. Anschließend addieren wir alle Ziffern stellenweise zusammen. Die Division wird gleichfalls schrittweise wie bei den Dezimalzahlen ausgeführt.Zugang bestellen
-
G32-5 Von der Binärzahl zur Dezimalzahl mittels Horner-SchemaDas Horner-Schema zerlegt Potenzen sinnvoll in Multiplikationen. Wiederholte Anwendung des Schemas in der Reihenfolge: mal 2, plus nächste Ziffer, Klammern herum. So erhalten wir den Dezimalwert der Binärzahl.Zugang bestellen
-
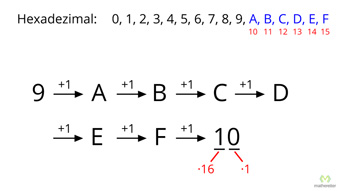
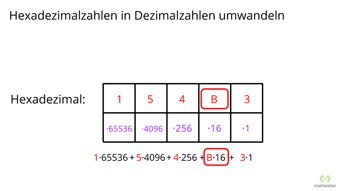
G32-6 Oktalzahlen und HexadezimalzahlenUmwandeln von Dezimalzahlen in Oktalzahlen und in Hexadezimalzahlen. Erklärung der einzelnen Schritte über die Summen von Potenzen. Zusätzlich die Umrechnung von Oktal- und Hexadezimalzahlen in Dezimalzahlen.Zugang bestellen
-
 15 minKlasse 9,10G33-1 Gauß-Verfahren - Grundlagen LGS, AdditionsverfahrenWas ist ein LGS (Lineares GleichungsSystem) und wie benutzt man es. Wie funktioniert das Additionsverfahren zum Lösen von LGS. Erlaubte Rechenmittel: Äquivalenzumformungen, Gleichungen miteinander addieren.Lektion öffnen
15 minKlasse 9,10G33-1 Gauß-Verfahren - Grundlagen LGS, AdditionsverfahrenWas ist ein LGS (Lineares GleichungsSystem) und wie benutzt man es. Wie funktioniert das Additionsverfahren zum Lösen von LGS. Erlaubte Rechenmittel: Äquivalenzumformungen, Gleichungen miteinander addieren.Lektion öffnen -
G33-2 Gauß-Verfahren - Lösung mit Gauß-VerfahrenLösen eines LGS mit Hilfe vom Gaußschen Eliminationsverfahren (kurz "Gauß-Verfahren"). Stufenweise Elimination/Beseitigung von Unbekannten, Stufenform.Zugang bestellen
-
G33-3 Gauß-Verfahren - Lösung mit KoeffizientenmatrixLösen eines LGS mittels Gauß-Verfahren und erweiterter Koeffizientenmatrix. Lösungsmöglichkeiten an letzter Zeile ablesbar. Lösungswege, wenn 0 der erste Koeffizient ist.Zugang bestellen
-
 4 minKlasse 8,9,10G34-1 Wie funktionieren Summen mit dem Summenzeichen?Was bedeutet das Summenzeichen Σ (Sigma)? Wie funktioniert die Notation mit dem Summenzeichen. Wir lernen kennen: Laufvariable mit Startwert, Endwert und Funktion zur Bildung der Summanden. Wir schauen uns die Summe der Quadratzahlen von 1 bis 5 mit Summenzeichen an.Lektion öffnen
4 minKlasse 8,9,10G34-1 Wie funktionieren Summen mit dem Summenzeichen?Was bedeutet das Summenzeichen Σ (Sigma)? Wie funktioniert die Notation mit dem Summenzeichen. Wir lernen kennen: Laufvariable mit Startwert, Endwert und Funktion zur Bildung der Summanden. Wir schauen uns die Summe der Quadratzahlen von 1 bis 5 mit Summenzeichen an.Lektion öffnen -
G34-2 Wie berechnet man Doppelsummen?Wir schauen uns Doppelsummen an: Was sind Doppelsummen, wie kann man damit rechnen? Erstes Beispiel Σ Σ n·k² mit Startwerten und Endwerten. Äußere und innere Summe. Zweites Beispiel: Σ Σ (i-1)·3^jZugang bestellen
-
 8 minKlasse 10G35-1 Rechentricks: Schnelle Division durch 5Wir zeigen euch einen Rechentrick, wie man die Division durch 5 sehr schnell berechnen kann. Statt :5 direkt zu rechnen, können wir es uns einfach machen und ·2:10 verwenden!Lektion öffnen
8 minKlasse 10G35-1 Rechentricks: Schnelle Division durch 5Wir zeigen euch einen Rechentrick, wie man die Division durch 5 sehr schnell berechnen kann. Statt :5 direkt zu rechnen, können wir es uns einfach machen und ·2:10 verwenden!Lektion öffnen -
 6 minKlasse 10G35-2 Rechentricks: Komma-Fünf-Zahlen quadrierenMit diesem Rechentrick könnt ihr Zahlen, die auf Komma Fünf enden (zum Beispiel die Zahl 9,5²), sehr schnell im Kopf quadrieren. Ohne Taschenrechner!Lektion öffnen
6 minKlasse 10G35-2 Rechentricks: Komma-Fünf-Zahlen quadrierenMit diesem Rechentrick könnt ihr Zahlen, die auf Komma Fünf enden (zum Beispiel die Zahl 9,5²), sehr schnell im Kopf quadrieren. Ohne Taschenrechner!Lektion öffnen -
 12 minKlasse 10G35-3 Rechentricks: Schnell von Netto zu BruttoMit diesem Rechentrick kommt ihr schnell von Netto zu Brutto. Mit nur einer Multiplikation verwandelt sich der Nettopreis in den Bruttopreis bzw. andersherum per Division. Ebenso lässt sich ein Preisnachlass schnell berechnen.Lektion öffnen
12 minKlasse 10G35-3 Rechentricks: Schnell von Netto zu BruttoMit diesem Rechentrick kommt ihr schnell von Netto zu Brutto. Mit nur einer Multiplikation verwandelt sich der Nettopreis in den Bruttopreis bzw. andersherum per Division. Ebenso lässt sich ein Preisnachlass schnell berechnen.Lektion öffnen -
 6 minKlasse 9,10G35-4 Rechne schneller im Kopf - LIVE gerechnetIn diesem Video lernt ihr, wie ihr schneller Kopfrechnen könnt. Die Rechnungen werden oben eingeblendet, damit ihr sie besser nachvollziehen könnt. Einfach Pause drücken und die Rechnung anschauen.Lektion öffnen
6 minKlasse 9,10G35-4 Rechne schneller im Kopf - LIVE gerechnetIn diesem Video lernt ihr, wie ihr schneller Kopfrechnen könnt. Die Rechnungen werden oben eingeblendet, damit ihr sie besser nachvollziehen könnt. Einfach Pause drücken und die Rechnung anschauen.Lektion öffnen -
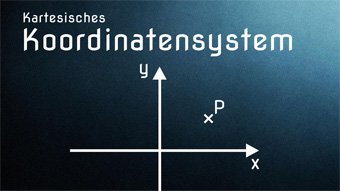 11 minKlasse 5F01-1 Kartesisches KoordinatensystemEinführung ins Kartesische Koordinatensystem. Wir betrachten uns x-Achse (Abszisse) und y-Achse (Ordinate), Punkte mit Koordinaten und die vier Quadranten.Lektion öffnen
11 minKlasse 5F01-1 Kartesisches KoordinatensystemEinführung ins Kartesische Koordinatensystem. Wir betrachten uns x-Achse (Abszisse) und y-Achse (Ordinate), Punkte mit Koordinaten und die vier Quadranten.Lektion öffnen -
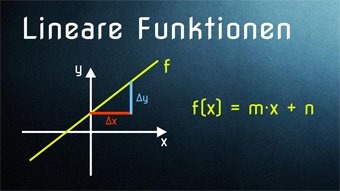
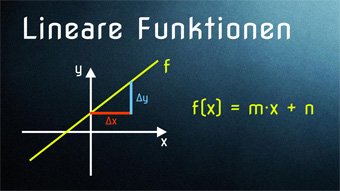
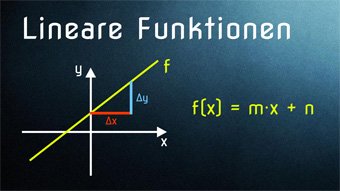
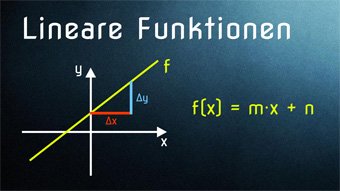
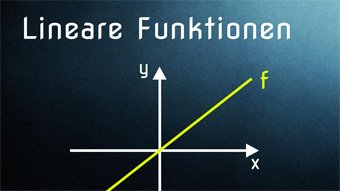 9 minKlasse 7,8F02-1 Lineare Funktionen - EinführungWas ist f(x), gesprochen "f von x". Wie entsteht eine Funktionsgleichung und wie ergibt sich die Steigung eines Graphen. Was ist ein Steigungsdreieck. Steigung einer linearen Funktion ermitteln.Lektion öffnen
9 minKlasse 7,8F02-1 Lineare Funktionen - EinführungWas ist f(x), gesprochen "f von x". Wie entsteht eine Funktionsgleichung und wie ergibt sich die Steigung eines Graphen. Was ist ein Steigungsdreieck. Steigung einer linearen Funktion ermitteln.Lektion öffnen -
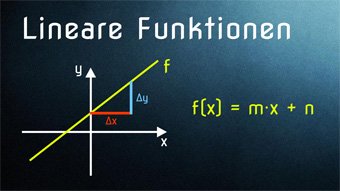 10 minKlasse 8F03-1 Lineare Funktion in Normalform - FunktionsgleichungFunktionsgleichung in Normalform f(x) = m·x + n, Lineare Gleichung, Schnittpunkt mit y-Achse, Steigung und SteigungsdreieckLektion öffnen
10 minKlasse 8F03-1 Lineare Funktion in Normalform - FunktionsgleichungFunktionsgleichung in Normalform f(x) = m·x + n, Lineare Gleichung, Schnittpunkt mit y-Achse, Steigung und SteigungsdreieckLektion öffnen -
F03-2 Lineare Funktion in Normalform - Gleichung aus 2 PunktenFunktion aus 2 Punkten ermitteln und Funktionsgleichung aufstellen (Schnittpunkt mit y-Achse und Steigung), Achsenschnittpunkte ermittelnZugang bestellen
-
F03-3 Lineare Funktion in Normalform - Konstante Funktion, NullstellenFunktionsgleichung und konstante Funktion, Nullstelle und Nullstellenberechnung, senkrechter FunktionsgraphZugang bestellen
-
F03-4 Gerade ins Koordinatensystem einzeichnen (Steigung)Wie zeichnet man eine Gerade in ein Koordinatensystem ein? Man hat eine Funktionsgleichung und soll diese als Graph zeichnen. Wir klären auf, wie man vorgeht und welche Verfahren es gibt.Zugang bestellen
-
F03-5 Liegt der Punkt auf dem Graphen (rechnerisch bestimmen)Ob ein Punkt auf einem Graphen liegt, lässt sich schnell überprüfen. In diesem kurzen Video zeigen wir, wie man das rechnerisch bestimmen kann.Zugang bestellen
-
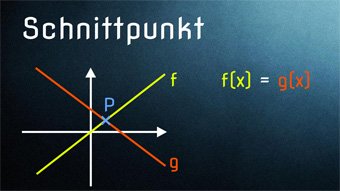
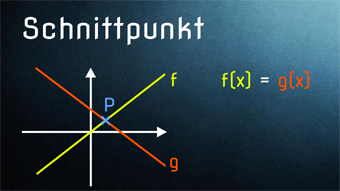
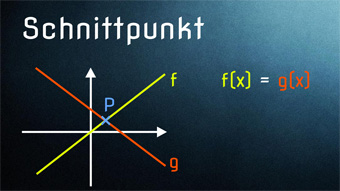
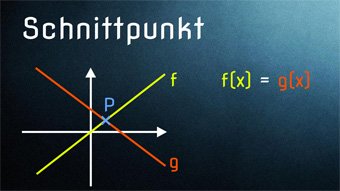 9 minKlasse 8F04-1 Schnittpunkt linearer Graphen - Lösen mit GleichsetzenSchnittpunkte von linearen Graphen finden, Funktionsgleichungen gleichsetzen zur Ermittlung des Schnittpunktes, lineare Gleichungen in Normalform ermittelnLektion öffnen
9 minKlasse 8F04-1 Schnittpunkt linearer Graphen - Lösen mit GleichsetzenSchnittpunkte von linearen Graphen finden, Funktionsgleichungen gleichsetzen zur Ermittlung des Schnittpunktes, lineare Gleichungen in Normalform ermittelnLektion öffnen -
F04-2 Schnittpunkt linearer Graphen - LösungsvariantenLösungsvarianten: 1 Schnittpunkt, kein Schnittpunkt, unendlich viele Schnittpunkte. Danach Lösung einer Bewegungsaufgabe: Aufstellen von Funktionsgleichungen zu Auto hat 100 km Vorsprung vor Motorrad.Zugang bestellen
-
F04-3 Zueinander orthogonale GeradenSchneiden sich zwei lineare Funktionsgraphen rechtwinklig, so spricht man von zueinander orthogonalen Geraden. Wir untersuchen Geraden auf Orthogonalität, indem wir ihre Steigungen betrachten.Zugang bestellen
-
F04-4 Zueinander orthogonale Geraden - HerleitungWir leiten her, weshalb beide Graphen senkrecht zueinander (orthogonal) sind, wenn ihre Steigungen multipliziert -1 ergeben. Anschließende Aufgabe: Orthogonale zu einer Geraden bestimmen, die durch einen bestimmten Punkt geht.Zugang bestellen
-
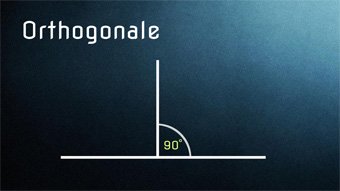 1 minKlasse 6,7,8F04-5 Was ist eine Orthogonale?Zwei Strecken (oder Geraden) sind orthogonal zueinander, wenn sie senkrecht aufeinander stehen. Andere Wörter für orthogonal: rechtwinklig, senkrecht. Schreibweise für zwei orthogonale Strecken a und b: a ⊥ bLektion öffnen
1 minKlasse 6,7,8F04-5 Was ist eine Orthogonale?Zwei Strecken (oder Geraden) sind orthogonal zueinander, wenn sie senkrecht aufeinander stehen. Andere Wörter für orthogonal: rechtwinklig, senkrecht. Schreibweise für zwei orthogonale Strecken a und b: a ⊥ bLektion öffnen -
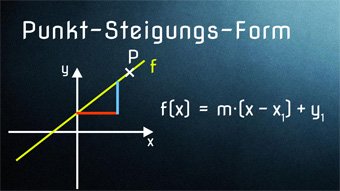
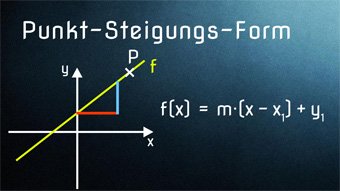
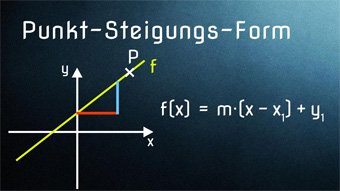 12 minKlasse 9F05-1 Gleichung einer linearen Funktion bestimmenWir zeigen, wie man mit Hilfe von 2 Punkten die Funktionsgleichung (Geradengleichung) eines linearen Graphen bestimmt. Anschließend Herleiten der Punkt-Steigungs-Form und Anwendung bei nur 1 Punkt und gegebener Steigung.Lektion öffnen
12 minKlasse 9F05-1 Gleichung einer linearen Funktion bestimmenWir zeigen, wie man mit Hilfe von 2 Punkten die Funktionsgleichung (Geradengleichung) eines linearen Graphen bestimmt. Anschließend Herleiten der Punkt-Steigungs-Form und Anwendung bei nur 1 Punkt und gegebener Steigung.Lektion öffnen -
F05-2 Gleichung bestimmen mit Punkt und ParallelenAufgabe zur Punkt-Steigungs-Form: Gleichung der Geraden bestimmen, die parallel zu einer anderen Geraden durch einen gegebenen Punkt verläuft. Erklärung der Bestandteile der Punkt-Steigungs-Form visuell im Koordinatensystem.Zugang bestellen
-
F05-3 Gleichung aus 2 Punkten bestimmen (LGS)Funktionsgleichung aus 2 Punkten ermitteln mit Hilfe vom Linearen Gleichungssystem und der Normalform. Anwendung von Gleichsetzungsverfahren und Subtraktionsverfahren.Zugang bestellen
-
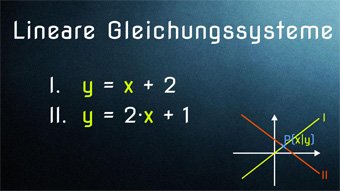 12 minKlasse 9F06-1 Lineare Gleichungssysteme - Die drei LösungsverfahrenDie 3 Lösungsverfahren in Kürze erklärt: Einsetzungsverfahren, Gleichsetzungsverfahren und AdditionsverfahrenLektion öffnen
12 minKlasse 9F06-1 Lineare Gleichungssysteme - Die drei LösungsverfahrenDie 3 Lösungsverfahren in Kürze erklärt: Einsetzungsverfahren, Gleichsetzungsverfahren und AdditionsverfahrenLektion öffnen -
F06-2 Lineare Gleichungssysteme - Einsetzung und GleichsetzungEinsetzungsverfahren und Gleichsetzungsverfahren im Detail, Schnittpunkt von Graphen, Lineare Gleichungssysteme (LGS) mittels Funktionen dargestelltZugang bestellen
-
F06-3 Lineare Gleichungssysteme - Additionsverfahren und FunktionenAdditionsverfahren mithilfe von Summenfunktion und Differenzfunktion erklärtZugang bestellen
-
F06-4 Lineare Gleichungssysteme - Lösen mit AdditionsverfahrenAdditionsverfahren im Detail, Lösen mit dem Additionsverfahren inklusive vorheriger Umformung der linearen GleichungenZugang bestellen
-
F06-5 Lineare Gleichungssysteme - SubtraktionsverfahrenAdditionsverfahren als Subtraktionsverfahren (Betrachtung als Differenzfunktion), mögliche Lösungen für lineare Gleichungssysteme (Lösungsmenge/Lösungspaar)Zugang bestellen
-
F06-6 Lineare Gleichungssysteme - SachaufgabeAnwendung des linearen Gleichungssystems bei einer Sachaufgabe (Stausee), Lösung mit dem SubtraktionsverfahrenZugang bestellen
-
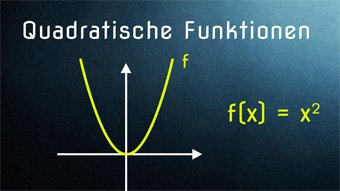
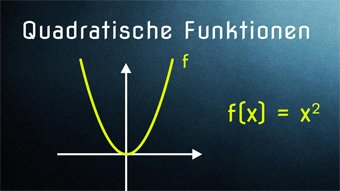
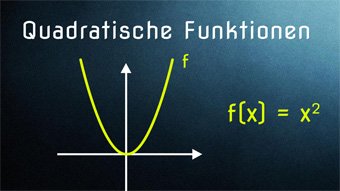
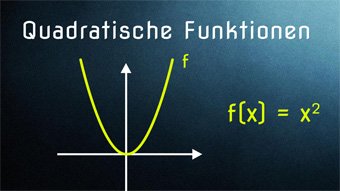
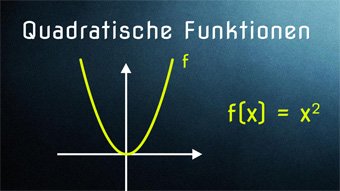
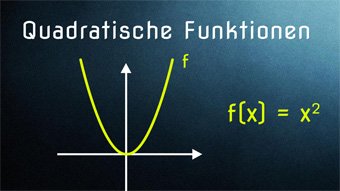
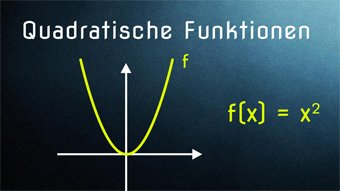
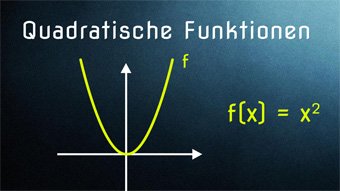 10 minKlasse 9F07-1 Quadratische Funktionen - Einführung ParabelEinführung zur Quadratischen Funktion über die Fläche eines Quadrats, Hinleitung zur Normalparabel, Streckung und Stauchung einer ParabelLektion öffnen
10 minKlasse 9F07-1 Quadratische Funktionen - Einführung ParabelEinführung zur Quadratischen Funktion über die Fläche eines Quadrats, Hinleitung zur Normalparabel, Streckung und Stauchung einer ParabelLektion öffnen -
F07-2 Quadratische Funktionen - Parabel und ScheitelpunktScheitelpunkt und Scheitelpunktform, Verschiebung der Parabel, Auswirkung von Streckung und Stauchung auf die Gleichung der FunktionZugang bestellen
-
F07-3 Quadratische Funktionen - Quadratische ErgänzungScheitelpunkt bestimmen, Scheitelpunktform und Allgemeinform, Erklärung der Quadratischen Ergänzung unter Anwendung der Binomischen Formeln.Zugang bestellen
-
F07-4 Quadratische Funktionen - Nullstellen bei ScheitelpunktformQuadratische Ergänzung bei einem Faktor vor x², Ermittlung von Nullstellen bei der ScheitelpunktformZugang bestellen
-
F07-5 Quadratische Funktionen - p-q-Formel und Nullstellenp-q-Formel zur Ermittlung der Nullstellen einer Quadratischen Funktion, Anwendung und HerleitungZugang bestellen
-
F07-6 Quadratische Funktionen - DiskriminanteBegriff Diskriminante, Lösungsmöglichkeiten bei der Diskriminante (p-q-Formel).Zugang bestellen
-
F07-7 Quadratische Funktionen - Satz von VietaHerleitung für den Satz von Vieta. Anwendungsbeispiele.Zugang bestellen
-
F07-8 Quadratische Funktionen - LinearfaktorenLinearfaktoren bei der Quadratischen Funktion, Funktionsgleichung aufstellen über Nullstellen und LinearfaktorenZugang bestellen
-
F07-9 Funktionsplotter + ZusammenfassungIn diesem Video erklären wir anhand eines Programms zum Zeichnen von Funktionen, wie sich die einzelnen Funktionen (0. bis 3. Grad) ergeben.Zugang bestellen
-
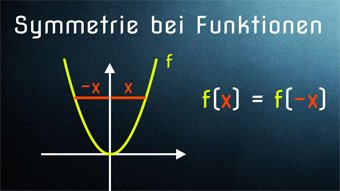
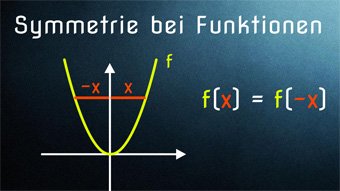
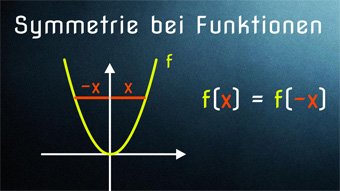 9 minKlasse 10F08-1 Symmetrie bei Funktionen - Achsen- u. PunktsymmetrieWir schauen uns die Symmetrie zur y-Achse f(x)=f(-x) und die Symmetrie zum Koordinatenursprung f(x)=-f(-x) an. Wir zeigen, wie man auf die Formeln kommt und wie man die Symmetrie am Graphen erkennt.Lektion öffnen
9 minKlasse 10F08-1 Symmetrie bei Funktionen - Achsen- u. PunktsymmetrieWir schauen uns die Symmetrie zur y-Achse f(x)=f(-x) und die Symmetrie zum Koordinatenursprung f(x)=-f(-x) an. Wir zeigen, wie man auf die Formeln kommt und wie man die Symmetrie am Graphen erkennt.Lektion öffnen -
F08-2 Symmetrie bei Funktionen - Symmetrie nachweisenWie kann man rechnerisch nachweisen, ob eine Funktion symmetrisch ist und welche Symmetrie vorliegt. Wie erkennt man bereits an der Funktionsgleichung die Symmetrieart (anhand der Exponenten). Begriffe: Gerade Funktion und ungerade Funktion. Koeffizienten beeinflussen Symmetrie nicht.Zugang bestellen
-
F08-3 Symmetrie bei Funktionen - Beliebige Senkrechte + PunktErmittlung der Formeln für die Symmetrie zu einer beliebigen Senkrechten f(a+x)=f(a-x) und zu einem beliebigen Punkt (Symmetriezentrum) mit f(a+x)-b = -f(a-x)+b. Übungsaufgaben zur Symmetrie. Symmetrie bei linearen Graphen, konstanter Funktion, Asymptote, Sinus- und Kosinusgraphen.Zugang bestellen
-
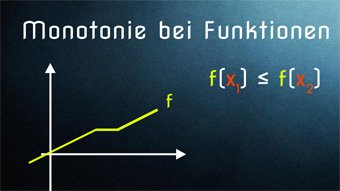
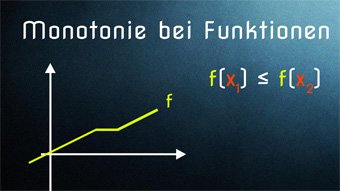 9 minKlasse 10F09-1 Monotonie bei Funktionen - EinführungWas ist Monotonie und wie bestimmen wir sie bei den Funktionen. Unterschied streng monoton steigend und monoton steigend. Beispiele für Graphen von streng monoton steigenden und fallenden Funktionen. Allgemeine Formel für Monotonie.Lektion öffnen
9 minKlasse 10F09-1 Monotonie bei Funktionen - EinführungWas ist Monotonie und wie bestimmen wir sie bei den Funktionen. Unterschied streng monoton steigend und monoton steigend. Beispiele für Graphen von streng monoton steigenden und fallenden Funktionen. Allgemeine Formel für Monotonie.Lektion öffnen -
F09-2 Monotonie bei Funktionen - Abschnittsweise FunktionenBestimmen des Monotonieverhaltens bei Funktionen mit Intervallen und Mengen. Was ist eine abschnittweise Funktion und wie definiert man diese bzw. ihre Abschnitte. Sonderfall der Monotonie bei konstantem Abschnitt.Zugang bestellen
-
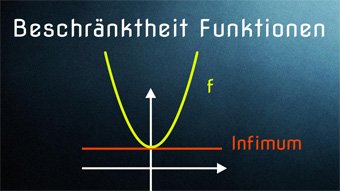
F10-1 Beschränktheit bei FunktionenWir untersuchen die Beschränktheit bei Funktionen. Wie ist eine Funktion nach oben und unten beschränkt. Beschränktheit im Intervall. Was sind Supremum und Infimum.Zugang bestellen
-
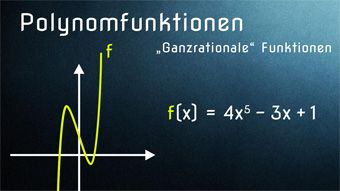 10 minKlasse 11F11-1 Polynomfunktionen - EinführungWas sind Polynomfunktionen (bzw. „ganzrationale Funktionen“). Was ist ein Polynom, was ist ein Koeffizient, was ist eine Polynomgleichung. Bekannte ganzrationale Funktionen: Lineare, Quadratische und Kubische Funktion. Hinweis: Was sind gebrochenrationale Funktionen.Lektion öffnen
10 minKlasse 11F11-1 Polynomfunktionen - EinführungWas sind Polynomfunktionen (bzw. „ganzrationale Funktionen“). Was ist ein Polynom, was ist ein Koeffizient, was ist eine Polynomgleichung. Bekannte ganzrationale Funktionen: Lineare, Quadratische und Kubische Funktion. Hinweis: Was sind gebrochenrationale Funktionen.Lektion öffnen -
F11-2 Polynomfunktionen - Nullstellen, SymmetrieHäufig ist es Aufgabe, die Nullstellen einer Polynomfunktion zu bestimmen. Verschiedene Lösungsverfahren helfen uns dabei. Namen von ganzrationalen Funktionen. Potenzfunktion. Symmetrie bei geraden und ungeraden Exponenten.Zugang bestellen
-
F11-3 Polynomfunktionen - UntersuchungWir untersuchen eine Polynomfunktion und bestimmen Funktionsgrad, Symmetrie, Punkte auf dem Graphen, wir zeichnen den Graphen und bestimmen Schnittpunkte und Berührungspunkte mit einer linearen Funktion sowie den Schnittwinkel mit der x-Achse.Zugang bestellen
-
F11-4 Was ist eine einfache, doppelte oder dreifache Nullstelle?Wie entstehen einfache, doppelte und dreifache Nullstellen. Welche Eigenschaften haben die Graphen. Wir lernen kennen: Achsenschnittpunkt, Berührpunkt, Sattelpunkt (Terrassenpunkt), Tangente, Linearfaktoren, Vielfachheit von NST. Sinusfunktion mit Berührpunkt.Zugang bestellen
-
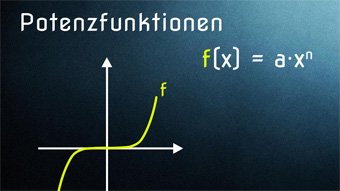
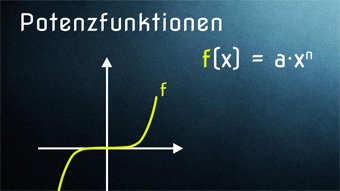
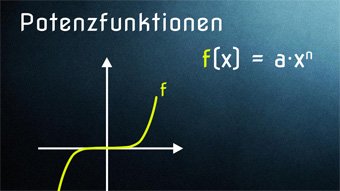
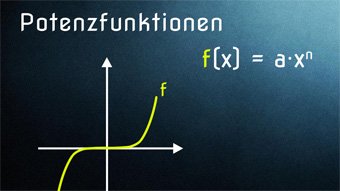 10 minKlasse 10,11F12-1 Potenzfunktionen: Symmetrie, Monotonie, Definitions-/WertebereichWas ist eine Potenzfunktion? Aufbau f(x) = a·x^n. Symmetrie bei geraden und ungeraden Exponenten (Achsensymmetrie und Punktsymmetrie). Gerade und ungerade Funktionen. Monotonieverhalten. Definitionsmenge und Wertebereich.Lektion öffnen
10 minKlasse 10,11F12-1 Potenzfunktionen: Symmetrie, Monotonie, Definitions-/WertebereichWas ist eine Potenzfunktion? Aufbau f(x) = a·x^n. Symmetrie bei geraden und ungeraden Exponenten (Achsensymmetrie und Punktsymmetrie). Gerade und ungerade Funktionen. Monotonieverhalten. Definitionsmenge und Wertebereich.Lektion öffnen -
F12-2 Potenzfunktionen: Gemeinsame Punkte, HyperbelGemeinsame Punkte bei Potenzfunktionen je nach geradem/ungeradem Exponent. Es entsteht eine Hyperbel, wenn der Exponent negativ wird, Beispiel: f(x)=x^(-1). Wie kommt es bei negativen Exponenten zur Definitionslücke bei x=0.Zugang bestellen
-
F12-3 Potenzfunktionen mit negativen ExponentenEigenschaften von Potenzfunktionen mit negativen Exponenten: Symmetrieverhalten, Monotonieverhalten, Definitionsmenge/Wertebereich, gemeinsame Punkte. Definitionslücken.Zugang bestellen
-
F12-4 Gleichung der Potenzfunktion aus 2 Punkten bestimmenWir bestimmen aus 2 gegebenen Punkten die Funktionsgleichung einer Potenzfunktion. Lösen per Logarithmus. Lösen mit Hilfe eines linearen Gleichungssystems.Zugang bestellen
-
F12-5 Schnittpunkte von 2 PotenzfunktionenWir berechnen die Schnittpunkte von 2 Potenzfunktionen mittels Gleichsetzen. x-Wert zu gegebenem Funktionswert bei einer Potenzfunktion ermitteln. Auswirkungen des Vorfaktors a bei f(x)=a·x^n auf den Graphen der Funktion.Zugang bestellen
-
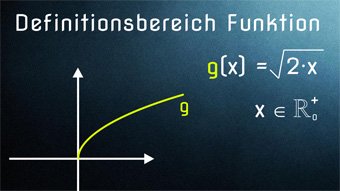 4 minKlasse 8,9,10F13-1 Definitionsbereich einer Funktion bestimmenWas ist der maximale Definitionsbereich (Definitionsmenge) einer Funktion und wie bestimmt man ihn. Wir wiederholen die Zahlenmengen und die Definition von Mengen, D = { x∈ ℝ: x ≥ 3 }. Einschränkung des Definitionsbereichs bei Wurzelgleichungen und Bruchgleichungen.Lektion öffnen
4 minKlasse 8,9,10F13-1 Definitionsbereich einer Funktion bestimmenWas ist der maximale Definitionsbereich (Definitionsmenge) einer Funktion und wie bestimmt man ihn. Wir wiederholen die Zahlenmengen und die Definition von Mengen, D = { x∈ ℝ: x ≥ 3 }. Einschränkung des Definitionsbereichs bei Wurzelgleichungen und Bruchgleichungen.Lektion öffnen -
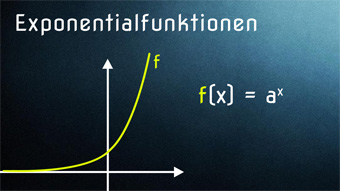
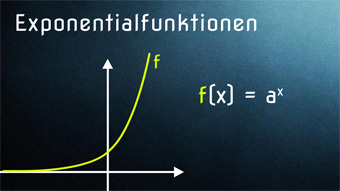
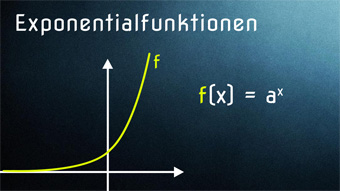
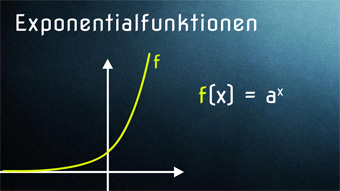
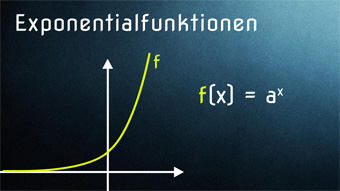 5 minKlasse 10F14-1 Exponentialfunktionen - Definition und GraphenWir definieren die Exponentialfunktion, legen die Definitionsmenge fest und schauen uns den Verlauf der Graphen an (gemeinsame Punkte, Monotonie).Lektion öffnen
5 minKlasse 10F14-1 Exponentialfunktionen - Definition und GraphenWir definieren die Exponentialfunktion, legen die Definitionsmenge fest und schauen uns den Verlauf der Graphen an (gemeinsame Punkte, Monotonie).Lektion öffnen -
F14-2 Exponentialfunktionen - Besondere Punkte, DefinitionsbereichWir untersuchen die Exponentialfunktionen und betrachten besondere Punkte und den Definitionsbereich.Zugang bestellen
-
F14-3 Exponentialfunktionen - Monotonie, Symmetrie, UmkehrfunktionMonotonieverhalten von Exponentialfunktionen entsprechend des Exponenten, Symmetrie, Nullstellen, Wachstum und Umkehrfunktion (Definition der Logarithmusfunktion).Zugang bestellen
-
F14-4 Exponentialfunktionen - Aufgabe Exponentielles WachstumAufgabe 1: Bestimmung von x per Logrithmus für f(x)=2^x. Aufgabe 2: Wann verzehnfachen sich Bakterien, Verdopplung je Stunde.Zugang bestellen
-
F14-5 Exponentialfunktionen - Exponentielle AbnahmeAufgabe 3: Exponentielle Abnahme/Zerfall von Lichtintensität. Aufgabe 4: Temperatur eines Tees sinkt, hierfür Funktionsgleichung aufstellen.Zugang bestellen
-
GEO01-1 Punkt, Strecke, Strahl, GeradeGeometrische Grundlagen: Punkt, Strecke, Strahl und Gerade.Zugang bestellen
-
 11 minKlasse 9,10GEO02-1 Kreis und Winkel - Der KreisDer Kreis: Entstehung und Definition des Kreises über Punkte und Polygon. Aufbau des Kreises, Elemente des Kreises. Bedeutung der Kreiszahl Pi. Berechnen von Kreisfläche und Kreisumfang.Lektion öffnen
11 minKlasse 9,10GEO02-1 Kreis und Winkel - Der KreisDer Kreis: Entstehung und Definition des Kreises über Punkte und Polygon. Aufbau des Kreises, Elemente des Kreises. Bedeutung der Kreiszahl Pi. Berechnen von Kreisfläche und Kreisumfang.Lektion öffnen -
GEO02-2 Kreis und Winkel - WinkelWinkel: Entstehung von Winkeln durch Drehung zweier Strahlen, Winkelmaße (Prozent, Grad, Bogenmaß), Winkelmessung mit dem Geo-Dreieck. Winkelarten und Winkelbezeichnungen. Winkel unter 0 Grad und über 360 Grad.Zugang bestellen
-
GEO02-3 Kreis und Winkel - Winkel an GeradenWinkel an zwei sich schneidenden Gerade. Gegenwinkel (Scheitelwinkel) und Nebenwinkel, Eigenschaften. Winkel an Parallelen: Stufen- und Wechselwinkel. Zusammenfassung.Zugang bestellen
-
GEO03-1 Dreiecke - GrundlagenGrundwissen zu den Dreiecken: Entstehung von Dreiecken, Dreiecksbeschriftung, Aufbau des Dreiecks, Dreiecksarten, Nachweis für den Winkelsummensatz 180°Zugang bestellen
-
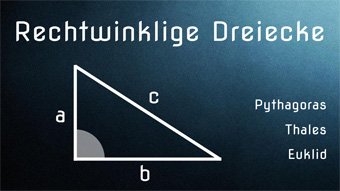
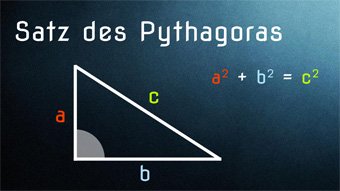
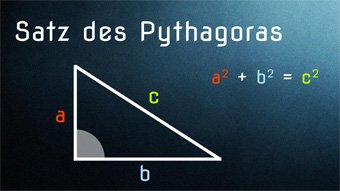
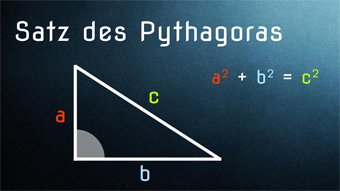
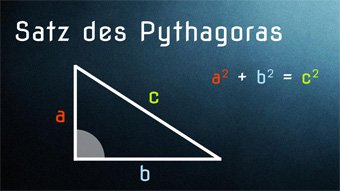
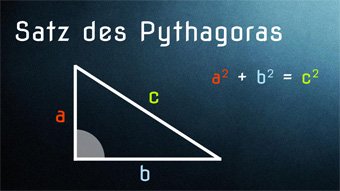
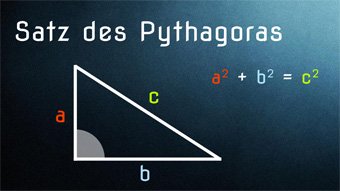
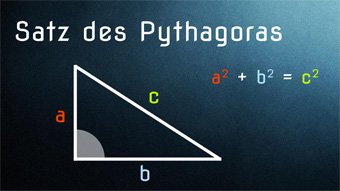
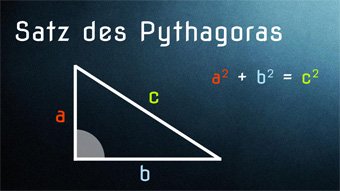
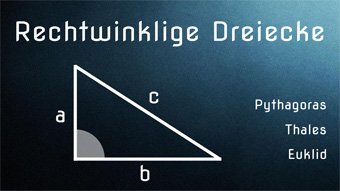
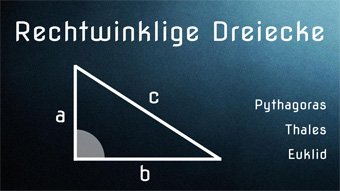
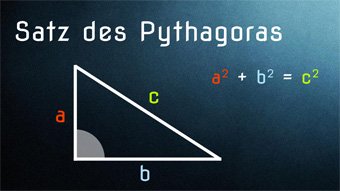 8 minKlasse 9,10GEO04-1 Satz des Pythagoras - Einführung und HerleitungDer Satz des Pythagoras für jeden einfach erklärt, mithilfe von Flächen und der ersten Binomischen Formel. Wir zeigen verschiedene Beweismöglichkeiten. Inklusive geometrischer Herleitung.Lektion öffnen
8 minKlasse 9,10GEO04-1 Satz des Pythagoras - Einführung und HerleitungDer Satz des Pythagoras für jeden einfach erklärt, mithilfe von Flächen und der ersten Binomischen Formel. Wir zeigen verschiedene Beweismöglichkeiten. Inklusive geometrischer Herleitung.Lektion öffnen -
GEO04-2 Satz des Pythagoras - Aufgaben, weitere NachweiseAnwendung vom Satz des Pythagoras, um fehlende Dreiecksseiten zu berechnen. Zudem zeigen wir zwei weitere Beweise.Zugang bestellen
-
GEO04-3 Prinzip hinter dem Satz des PythagorasDas Prinzip des Pythagoras funktioniert auch für Dreiecke, Rechtecke, Kreise u.a. In diesem Video zeigen wir, warum das so ist und welcher Mechanismus sich dahinter verbirgt.Zugang bestellen
-
GEO04-4 Satz des Pythaogras zum LegenWir schauen uns den Satz des Pythagoras mit Montessori-Material an und legen die Quadrate so, dass die Flächen mit a² + b² = c² erkennbar werden.Zugang bestellen
-
GEO04-5 Satz des Pythagoras erkennenAufgabenvideo: Gib die Hypotenuse für das rechtwinklige Dreieck an und notiere die Formel für den Satz des Pythagoras.Zugang bestellen
-
GEO04-6 Rechtwinklige Dreiecke bestimmenAufgabenvideo: Prüfe mit dem Satz des Pythagoras, ob die Dreiecke rechtwinklig sind.Zugang bestellen
-
GEO04-7 Dreiecksseiten mit Pythagoras berechnenAufgabenvideo: Wir verwenden den Satz des Pythagoras, um die Seitenlängen im rechtwinkligen Dreieck zu berechnen. Gegeben sind zwei Seiten.Zugang bestellen
-
GEO04-8 Pythagoras in FigurenAufgabenvideo: Mit dem Satz des Pythagoras berechnen wir die Flächendiagonalen von Quadrat und Rechteck.Zugang bestellen
-
GEO04-9 Pythagoras in KörpernAufgabenvideo: Mit dem Satz des Pythagoras berechnen wir Flächendiagonale und Raumdiagonale im Würfel.Zugang bestellen
-
GEO05-1 Satz des ThalesNachweis für den Satz des Thales: Es ergibt sich stets ein rechtwinkliges Dreieck, wenn man den Durchmesser des Kreises als Grundseite betrachtet und einen weiteren Dreieckspunkt auf die Kreislinie setzt.Zugang bestellen
-
GEO05-2 Höhensatz und Kathetensatz EuklidWir zeigen, wie man die Höhe, und die Teilstrecken p und q berechnet. Dabei stoßen wir auf den Höhensatz und den Kathetensatz des Euklid.Zugang bestellen
-
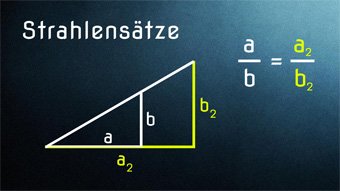 11 minKlasse 8,9GEO06-1 StrahlensätzeDie Strahlensätze werden hier ausführlich erklärt. Wir setzen die Seiten zueinander ins Verhältnis und weisen die Beziehungen zueinander nach. Zentrische Streckung, Ähnlichkeit.Lektion öffnen
11 minKlasse 8,9GEO06-1 StrahlensätzeDie Strahlensätze werden hier ausführlich erklärt. Wir setzen die Seiten zueinander ins Verhältnis und weisen die Beziehungen zueinander nach. Zentrische Streckung, Ähnlichkeit.Lektion öffnen -
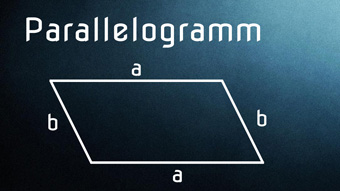
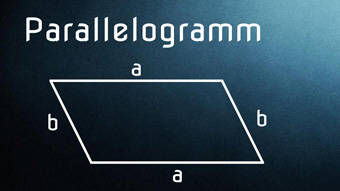
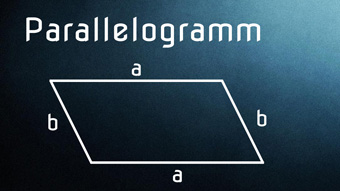 3 minKlasse 7,8,9,10GEO07-1 Was ist ein ParallelogrammZuerst klären wir, was Parallelogramm heißt, dann definieren wir die geometrische Figur als Viereck, dessen gegenüberliegende Seiten zueinander parallel sind.Lektion öffnen
3 minKlasse 7,8,9,10GEO07-1 Was ist ein ParallelogrammZuerst klären wir, was Parallelogramm heißt, dann definieren wir die geometrische Figur als Viereck, dessen gegenüberliegende Seiten zueinander parallel sind.Lektion öffnen -
GEO07-2 Parallelogramm - Umfang und FlächeninhaltWir leiten die Formeln für Umfang und Flächeninhalt des Parallelogramms her. Vorher lernen wir, dass Winkel α und β immer 180° ergeben und schauen uns die Höhen im Paralellogramm an. Vergleich Rechteck mit Parallelogramm.Zugang bestellen
-
GEO07-3 Parallelogramm - Formeln für HöhenWir leiten die Formeln für die Höhen h_a und h_b im Parallelogramm her. Dazu verwenden wir den Sinus.Zugang bestellen
-
GEO07-4 Parallelogramm - Formeln für DiagonalenWir leiten die Formeln für die Diagonalen e und f her. Dazu verwenden wir den Kosinussatz und die Wurzel. Auch rechnen wir eine Beispielaufgabe, bei der wir e aus den Seiten a, b und dem Winkel β bestimmen.Zugang bestellen
-
GEO07-5 Parallelogramm - Flächenformel II + SonderformenWir schauen uns eine zweite Flächenformel für das Parallelogramm an, die nur Seiten a und b und den Sinus von Winkel α benötigt. Danach lernen wir Sonderformen des Parallelogramms kennen: Rechteck, Quadrat, Raute.Zugang bestellen
-
GEO07-6 Parallelogramm - Aufgabe: Seiten bestimmenWir rechnen eine Übungsaufgabe: Aus gegebenem Flächeninhalt, Höhe a und Winkel α bestimmen wir die Seiten a und b. Wir besprechen, wie man bei solchen Aufgaben vorgeht.Zugang bestellen
-
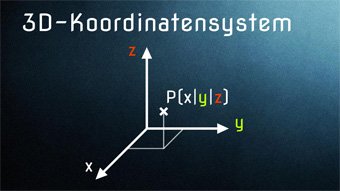
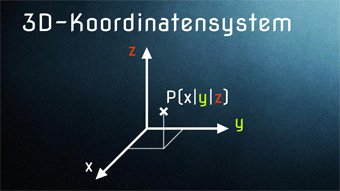
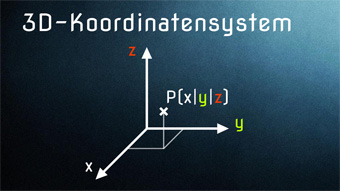 12 minKlasse 7,8STE01-1 3D-Koordinatensystem / Koordinatenebenen / Punkte im RaumWas ist Stereometrie (Raumgeometrie). Wie ist die Dimension definiert. Wir stellen 2D- und 3D-Koordinatensystem gegenüber. Einzeichnen von Punkten in 3D (Breite, Länge, Höhe). Quader in 3D. Wir lernen die Ebene und Koordinatenebenen kennen. 8 Oktanten. Rechtssystem/Linkssystem.Lektion öffnen
12 minKlasse 7,8STE01-1 3D-Koordinatensystem / Koordinatenebenen / Punkte im RaumWas ist Stereometrie (Raumgeometrie). Wie ist die Dimension definiert. Wir stellen 2D- und 3D-Koordinatensystem gegenüber. Einzeichnen von Punkten in 3D (Breite, Länge, Höhe). Quader in 3D. Wir lernen die Ebene und Koordinatenebenen kennen. 8 Oktanten. Rechtssystem/Linkssystem.Lektion öffnen -
STE01-2 Koordinaten von Punkten im Raum bestimmenKoordinaten von Punkten im 3D-Koordinatensystem ablesen. Koordinatenquader als Hilfe zum Ablesen. Namen der Achsen x, y, z oder x₁, x₂, x₃.Zugang bestellen
-
STE01-3 Schrägbild zeichnen auf KaropapierWir zeichnen einen Quader auf das Blatt Papier, also Karopapier wie im Unterricht. Breite und Höhe werden direkt eingetragen, die Länge nach hinten mit 45 Grad und halbiert.Zugang bestellen
-
STE01-4 3D-Koordinatensystem zeichnen und DreieckWie zeichnet man ein 3D-Koordinatensystem auf das Blatt Papier. Die y-Achse waagerecht, die z-Achse senkrecht, die x-Achse meist im Winkel von 45 Grad. Einteilung der x-Achse. Eintragen von Punkten, erstellen eines Dreiecks. Vorstellung Hilfsprogramm Schrägbildzeichner.Zugang bestellen
-
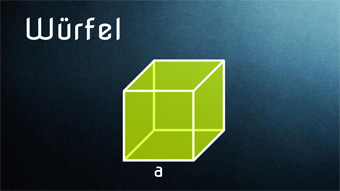
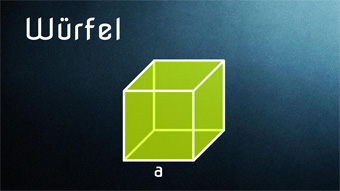
STE02-1 Würfel - Bestandteile, FlächenberechnungWas ist ein Würfel. Bestandteile: Kante, Flächendiagonale, Raumdiagonale, Umfang, Grundfläche, Mantelfläche, Oberfläche, Volumen. Berechnung aller Flächen und des Umfangs.Zugang bestellen
-
STE02-2 Würfel - Flächendiagonale, RaumdiagonaleHerleitung der Formeln für die Flächendiagonale und die Raumdiagonale mit Hilfe vom Satz des Pythagoras. Formel für Länge aller Seitenkanten des Würfels.Zugang bestellen
-
STE02-3 Würfel - Volumen, Bestimmen aller WerteWie ergibt sich das Würfelvolumen. Dann schauen wir uns an, wie wir von einem gegebenen Würfelwert auf alle anderen Werte kommt. Wir müssen stets auf die Kante zurückrechnen.Zugang bestellen
-
STE03-1 Quader - Einführung und BestandteileWas ist ein Quader. Bestandteile: 12 Seiten, 8 Ecken, 6 Flächen. Flächendiagonale, Raumdiagonale, Volumen. Definition des Körpers.Zugang bestellen
-
STE03-2 Quader - Herleitung aller FormelnHerleitung der Formeln für Umfang, Grundfläche, Mantelfläche, Oberfläche, Volumen, Flächendiagonalen, Raumdiagonalen. Wir nutzen den Satz des Pythagoras.Zugang bestellen
-
STE03-3 Quader - Fehlende Seite berechnenÜbungsaufgaben: Mantefläche bzw. Oberfläche und 2 Seiten gegeben, fehlende Seite ermitteln. Volumen und 2 Seiten gegeben, fehlende Seite ermitteln.Zugang bestellen
-
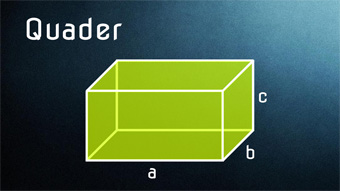 9 minKlasse 6,7,8STE03-4 Volumen des Quaders berechnenVolumen eines Quaders aus Höhe, Breite und Länge bestimmen. 1m³-Würfel zur besseren Vorstellung des Quader-Volumens. Volumenformel V=b·h·t leichter merken. Wann ist das Volumen Null.Lektion öffnen
9 minKlasse 6,7,8STE03-4 Volumen des Quaders berechnenVolumen eines Quaders aus Höhe, Breite und Länge bestimmen. 1m³-Würfel zur besseren Vorstellung des Quader-Volumens. Volumenformel V=b·h·t leichter merken. Wann ist das Volumen Null.Lektion öffnen -
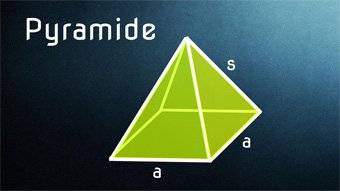 9 minKlasse 8,9,10STE04-1 Quadratische Pyramide - Bestandteile, Herleitung FormelnBestandteile der Pyramide: Seite a, Höhe der Pyramide h, Seitenkante s, Höhe auf Seite a, Diagonale d, Grundfläche, Seitenfläche, Oberfläche, Volumen. Herleitung der Formeln für die Seitenkante s und die Höhe h_a sowie für die Diagonale. Unterschied gerade und schiefe Pyramide.Lektion öffnen
9 minKlasse 8,9,10STE04-1 Quadratische Pyramide - Bestandteile, Herleitung FormelnBestandteile der Pyramide: Seite a, Höhe der Pyramide h, Seitenkante s, Höhe auf Seite a, Diagonale d, Grundfläche, Seitenfläche, Oberfläche, Volumen. Herleitung der Formeln für die Seitenkante s und die Höhe h_a sowie für die Diagonale. Unterschied gerade und schiefe Pyramide.Lektion öffnen -
STE04-2 Quadratische Pyramide - Herleitung Flächenformeln, VolumenWir leiten die Formeln für Umfang, Grundfläche, Mantelfläche, Oberfläche her. Wir zeigen, wie die Volumenformel lautet und wie man sie sich besser merken kann. Am Ende fassen wir alle Formeln zu den Pyramiden zusammen.Zugang bestellen
-
STE04-3 Quadratische Pyramide - AufgabenZuerst Übersicht aller Formeln. Dann lösen wir die Aufgabe: Gegeben sind Höhe h und Seite a und wir berechnen alle Bestandteile der Pyramide. Nächste Aufgabe: Es sind nur Seite a und Oberfläche gegeben, die Höhe ist zu bestimmen.Zugang bestellen
-
STE04-4 Quadratische Pyramide - Aufgaben IIWir stellen eine Formel für Seite a auf, wenn nur Seitenkante s und Mantelfläche M gegeben sind. Wir substituieren und prüfen auf Scheinlösungen, um das korrekte Ergebnis zu ermitteln.Zugang bestellen
-
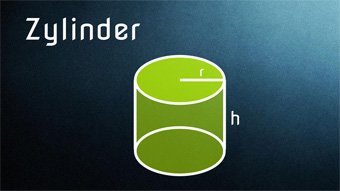
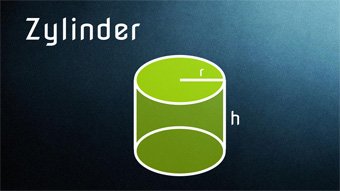 11 minKlasse 9,10STE05-1 Einführung Zylinder - Gerader KreiszylinderBestandteile des Zylinders: Radius, Höhe, Durchmesser, Umfang, Grundfläche, Deckfläche, Mantelfläche, Oberfläche, Volumen. Zylinderarten. Beispiele aus dem Alltag für gerade Kreiszylinder. Herleitung aller Zylinderformeln.Lektion öffnen
11 minKlasse 9,10STE05-1 Einführung Zylinder - Gerader KreiszylinderBestandteile des Zylinders: Radius, Höhe, Durchmesser, Umfang, Grundfläche, Deckfläche, Mantelfläche, Oberfläche, Volumen. Zylinderarten. Beispiele aus dem Alltag für gerade Kreiszylinder. Herleitung aller Zylinderformeln.Lektion öffnen -
STE05-2 Kreiszylinder berechnen aus Radius und HöheWir berechnen alle Bestandteile (Strecken, Flächen, Volumen) eines geraden Kreiszylinders aus gegebenen Werten zu Radius und Höhe. Berechnung aller Zylinderwerte aus Radius und Oberfläche.Zugang bestellen
-
STE05-3 Kreiszylinder berechnen aus Umfang und MantelflächeBei vielen Aufgaben sind Radius und Höhe nicht gegeben. Hier müssen wir beide aus gegebenen Formeln ermitteln (Beispiel für Umfang und Mantelfläche). Danach Sachaufgabe zu zylinderförmigen Glas (bekannt sind Höhe und Volumen).Zugang bestellen
-
STE05-4 Zylinderformel aufstellen aus Höhe und OberflächeWir stellen die Formel für den Radius auf, wenn nur Höhe und Oberfläche gegeben sind. Danach Sachaufgabe zu Gewicht eines zylindrischen Rundstahls.Zugang bestellen
-
STE05-5 Zylinderformel aufstellen aus Grundfläche und OberflächeWir betrachten uns, wie sich die Formeln für den Radius und die Höhe ergeben, wenn nur Grundfläche und Oberfläche bekannt sind.Zugang bestellen
-
STE05-6 Volumen eines Hohlzylinders berechnenWas ist ein Hohlzylinder. Berechnung des Volumens eines Hohlzylinders. Wir stellen die Formel dazu auf. Umrechnung von mm³ zu cm³.Zugang bestellen
-
STE05-7 Zylinderaufgaben selbst schnell lösenWir zeigen euch anhand einer Aufgabe (Zylinderbohrung im Quader), wie ihr Aufgaben selbst mit den Matheprogrammen lösen könnt. Wir verwenden dazu Tinkercad, Google Docs, Taschenrechner und Assistenzrechner.Zugang bestellen
-
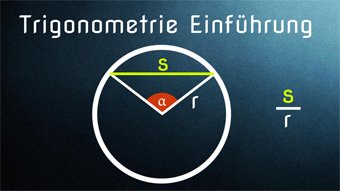 15 minKlasse 9,10TRI01-1 Einführung zur TrigonometrieBedeutung des Begriffs "Trigonometrie", Blick in die Geschichte, Sehne am Kreis (Chord), Halbe Sehne als Vorgänger des Sinus, Anwendungsgebiete der TrigonometrieLektion öffnen
15 minKlasse 9,10TRI01-1 Einführung zur TrigonometrieBedeutung des Begriffs "Trigonometrie", Blick in die Geschichte, Sehne am Kreis (Chord), Halbe Sehne als Vorgänger des Sinus, Anwendungsgebiete der TrigonometrieLektion öffnen -
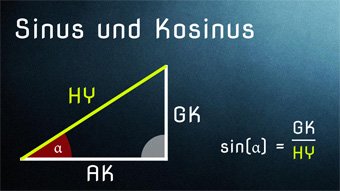
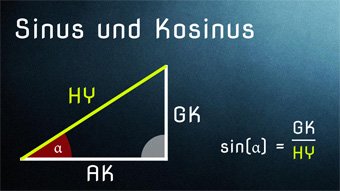
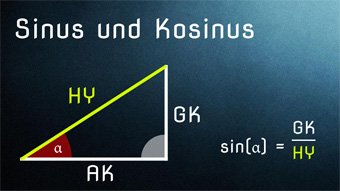
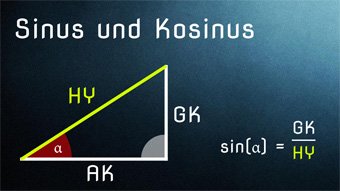 12 minKlasse 9,10TRI02-1 Sinus und Kosinus - EinführungWir klären die Begriffe Gegenkathete, Ankathete und Hypotenuse. Danach untersuchen wir die Seitenverhältnisse im rechtwinkligen Dreieck, die zu Sinus und Kosinus führen.Lektion öffnen
12 minKlasse 9,10TRI02-1 Sinus und Kosinus - EinführungWir klären die Begriffe Gegenkathete, Ankathete und Hypotenuse. Danach untersuchen wir die Seitenverhältnisse im rechtwinkligen Dreieck, die zu Sinus und Kosinus führen.Lektion öffnen -
TRI02-2 Sinus und Kosinus - Winkel und SeitenverhältnisseBei einer Hypotenuse der mit Länge 1 können wir Sinus und Kosinus an den Katheten ablesen. Wir betrachten Werte für Sinus und Kosinus bei 0° bis 90° und wie wir (Ko)Sinus an x- und y-Achse ablesen können + Sinus-Tabelle.Zugang bestellen
-
TRI02-3 Sinus und Kosinus - Anwendung DreiecksberechnungWir berechnen Aufgaben, bei denen nur 1 Dreiecksseite und 1 Winkel gegeben ist. Nach dem Video werdet ihr alle rechtwinkligen Dreiecke mit Hilfe des Sinus oder des Kosinus berechnen können!Zugang bestellen
-
TRI02-4 Sinus und Kosinus - Arkussinus und ArkuskosinusKurze Zusammenfassung, danach: Arkussinus sin^(-1) bzw. Arkuskosinus cos^(-1) zur Bestimmung des Winkels aus zwei Dreiecksseiten. Wortherkunft der Begriffe Sinus und Kosinus.Zugang bestellen
-
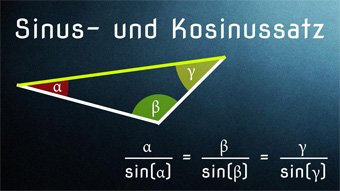
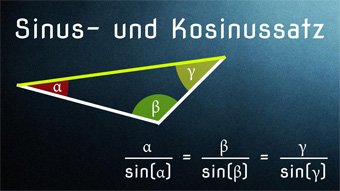
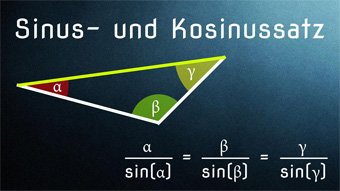
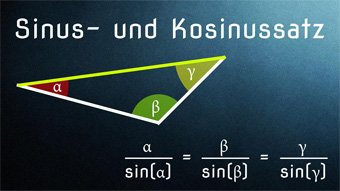
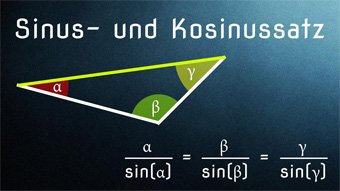
TRI03-1 Sinus+Kosinus bei Dreiecken - SinussatzHerleitung vom Sinussatz, Berechnen von Beispielen im allgemeinen Dreieck, Seiten und Winkel bestimmen mit Hilfe des Sinussatzes: a / sin(α) = b / sin(β) = c / sin(γ)Zugang bestellen
-
TRI03-2 Sinus+Kosinus bei Dreiecken - Sinus u. Kosinus bis 180 GradHöhe des Allgemeinen Dreiecks als Gegenkathete, Sinus-Werte von 90° bis 180°, Identitäten sin(α) = sin(180-α), cos(α) = -cos(180-α), Anwendung Sinussatz am stumpfwinkligen Dreieck.Zugang bestellen
-
 11 minKlasse 9,10TRI03-3 Sinus+Kosinus bei Dreiecken - Kosinussatz inkl. HerleitungHerleitung des Kosinussatzes mit Hilfe vom Satz des Pythagoras und dem Kosinus. Bei gegebenen 2 Seiten und eingeschlossenem Winkel kann mit dem Kosinussatz die 3. Dreiecksseite bestimmt werden. Eselsbrücke fürs leichtere Merken der Formel.Lektion öffnen
11 minKlasse 9,10TRI03-3 Sinus+Kosinus bei Dreiecken - Kosinussatz inkl. HerleitungHerleitung des Kosinussatzes mit Hilfe vom Satz des Pythagoras und dem Kosinus. Bei gegebenen 2 Seiten und eingeschlossenem Winkel kann mit dem Kosinussatz die 3. Dreiecksseite bestimmt werden. Eselsbrücke fürs leichtere Merken der Formel.Lektion öffnen -
TRI03-4 Sinus+Kosinus bei Dreiecken - Kosinussatz über FlächenIn diesem Video leiten wir den Kosinussatz über die Flächenformel her. Abschließend zeigen wir, unter welchen Umständen aus dem Kosinussatz der Satz des Pythagoras wird.Zugang bestellen
-
TRI03-5 Sinus+Kosinus bei Dreiecken - Kosinussatz Winkel berechnenAnwendung des Kosinussatzes zur Dreiecksberechnung, Ermittlung des unbekannten Winkels aus 3 Dreiecksseiten, Zusammenfassung und Falleinteilung, wann der Sinussatz oder der Kosinussatz anzuwenden ist.Zugang bestellen
-
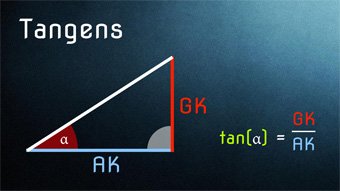
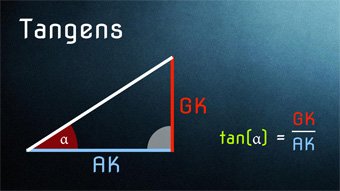
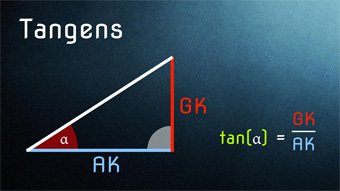
TRI04-1 Tangens - Einfache EinführungWas ist der Tangens, wie ist er definiert. Was bedeutet das Seitenverhältnis Gegenkathete zu Ankathete. Anwendung des Tangens zur Seitenbestimmung und Anwendung des Arkustangens zur Winkelbestimmung.Zugang bestellen
-
TRI04-2 Tangens - Tangens für Winkel von 0° bis 180°Tangens von 0° bis 180° im Koordinatensystem ablesen, besondere Tangenswerte für 0°, 90° und 180°. Negativer Tangens. Tangens als Steigung. Ermittlung der Steigung einer linearen Funktion mit Hilfe des Tangens.Zugang bestellen
-
TRI04-3 Tangens - Zusammenfassung + Aufgaben lösenZusammenfassung des neuen Wissens. Tangens als Sinus/Kosinus. Aufgaben: Höhenbestimmung aus Winkel und Distanz. Winkelbestimmung aus Höhe und Distanz. Wann nutzt man Sinus, Kosinus oder Tangens.Zugang bestellen
-
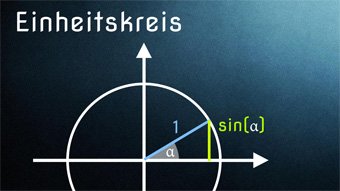
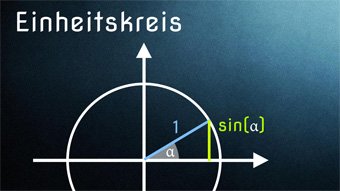
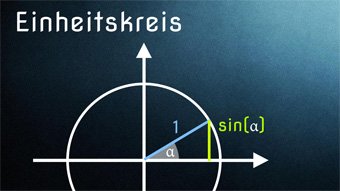
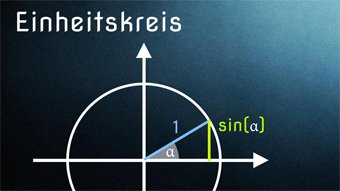
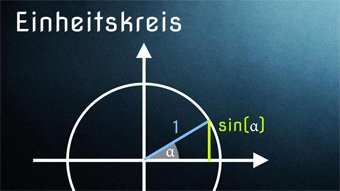 14 minKlasse 9,10TRI05-1 Einheitskreis - Einführung Einheitskreis mit Sinus und KosinusEinheitskreis zur Ermittlung von Sinus und Kosinus für beliebige Winkel. Wie können wir die Werte für sin und cos am Einheitskreis ablesen. Zusätzlich klären wir die Wortherkunft "Einheitskreis". Wir zeigen, wie ihr euch wichtige Sinus- und Kosinuswerte merken könnt.Lektion öffnen
14 minKlasse 9,10TRI05-1 Einheitskreis - Einführung Einheitskreis mit Sinus und KosinusEinheitskreis zur Ermittlung von Sinus und Kosinus für beliebige Winkel. Wie können wir die Werte für sin und cos am Einheitskreis ablesen. Zusätzlich klären wir die Wortherkunft "Einheitskreis". Wir zeigen, wie ihr euch wichtige Sinus- und Kosinuswerte merken könnt.Lektion öffnen -
TRI05-2 Einheitskreis - Referenzdreieck, PunktkoordinatenWann sind Sinus und Kosinus positiv und negativ. Sinus und Kosinus lassen sich mit Referenzdreiecken für jeden Quadranten des Koordinatensystems bestimmen. Wertebereich für Sinus und Kosinus. (Ko)Sinus ablesen an den Punktkoordinaten des Winkels.Zugang bestellen
-
TRI05-3 Einheitskreis - Tangens am EinheitskreisTangens für beliebige Winkel mit Hilfe des Einheitskreises. Im Gegensatz zum Sinus und Kosinus kann der Tangens bei bestimmten Winkeln "nicht definiert" sein. Positive und negative Tangenswerte je nach Quadrant. Tangens mit Punktkoordinaten berechnen.Zugang bestellen
-
TRI05-4 Einheitskreis - Identitäten zur WinkelbestimmungWinkel (0° bis 360°) aus Sinus- und Kosinuswert bestimmen. Was sind Identitäten. Wir behandeln eine Auswahl an Identitäten inkl. Anwendung. Deutung des Kosinus als um 90° rotierter Sinus. Warum heißt Kosinus Ko-Sinus.Zugang bestellen
-
TRI05-5 Einheitskreis - Trigonometrischer PythagorasSchreibweise sin²(a) für (sin(a))². Herleitung des trigonometrischen Pythagoras: cos²(a) + sin²(a) = 1 sowie der Koordinatengleichung des Einheitskreises x² + y² = 1. Vom Winkel und Sinuswert rechnerisch zu dessen Kosinuswert.Zugang bestellen
-
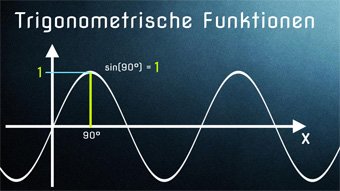
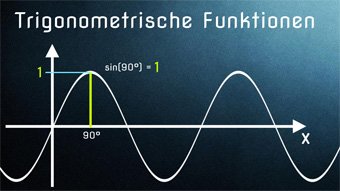
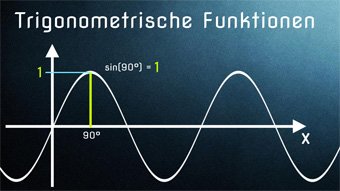
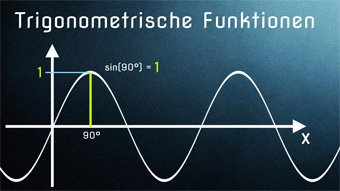
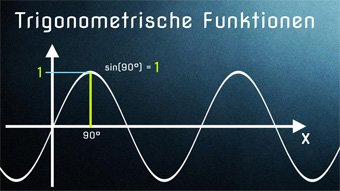 15 minKlasse 10TRI06-1 Trigonometrische Funktionen - Einführung SinusfunktionWas bedeutet Sinus-Funktion, wie ergibt sie sich? Wir stellen die Sinusfunktion im Koordinatensystem dar und erhalten einen geschwungenen Graphen (Sinuskurve). Beispiel aus dem Alltag: Beschreibung der Flughöhe eines Balles, der an einer Feder befestigt ist.Lektion öffnen
15 minKlasse 10TRI06-1 Trigonometrische Funktionen - Einführung SinusfunktionWas bedeutet Sinus-Funktion, wie ergibt sie sich? Wir stellen die Sinusfunktion im Koordinatensystem dar und erhalten einen geschwungenen Graphen (Sinuskurve). Beispiel aus dem Alltag: Beschreibung der Flughöhe eines Balles, der an einer Feder befestigt ist.Lektion öffnen -
TRI06-2 Trigonometrische Funktionen - Kosinusfunktion + PeriodeWie ergibt sich die Kosinusfunktion? Einführung der Periode bei Sinus und Kosinus. Darstellung der (Ko)Sinusfunktion im Einheitskreis. Kosinus-Schwingung am Beispiel des Pendels! Lineare Bewegung kontra Kosinusschwingung.Zugang bestellen
-
TRI06-3 Trigonometrische Funktionen - TangensfunktionWie ergibt sich die Tangensfunktion? Der Tangensgraph unterscheidet sich vom (Ko)Sinusgraphen. Auch klären wir, wie man die Periode der Sinus-, Kosinus- und Tangensfunktion notiert, für Sinus: sin(α) = sin(α + k·360°)Zugang bestellen
-
TRI06-4 Trigonometrische Funktionen - Allgemeine SinusfunktionWie lässt sich die Sinusfunktion verändern? Wir betrachten die Funktionsgleichung f(x) = a·sin(b·x + c) + d und klären die Bedeutung der einzelnen Variablen. Wir strecken und stauchen den Sinusgraphen und spiegeln ihn.Zugang bestellen
-
TRI06-5 Trigonometrische Funktionen - Kosinus- und TangensfunktionWir verschieben die Sinusfunktion entlang der Achsen und schauen uns an, wie sich die Kosinus- und Tangensfunktion verändern lassen. Auch klären wir in diesem Zusammenhang die Begriffe Amplitude, (Kreis)Frequenz und Phasenverschiebung.Zugang bestellen
-
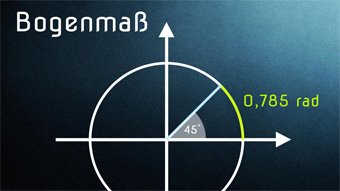
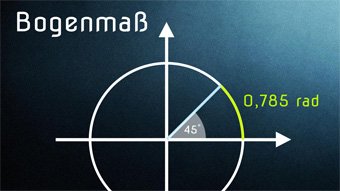
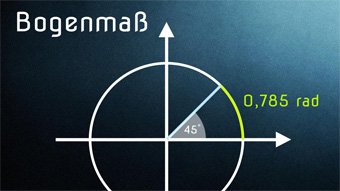
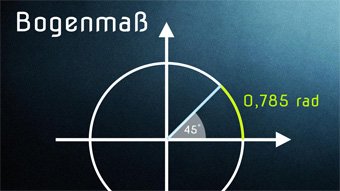
TRI07-1 Bogenmaß - EinführungWiederholung der Winkelmaße. Definition von Bogenmaß mit α = Kreisbogen / Kreisradius. Einheit: Radiant. Zusammenhang zwischen Bogenmaß und Kreiszahl Pi.Zugang bestellen
-
TRI07-2 Bogenmaß - Bogenmaß und Grad umrechnenWie rechnen wir Grad in Bogenmaß um. Wie lässt sich Pi hierzu benutzen? Herleitung der Umrechnungsformeln. Abschließend 2 Aufgaben zur Umrechnung Grad ↔ Bogenmaß.Zugang bestellen
-
TRI07-3 Bogenmaß - Bogenmaß mit dem TaschenrechnerAuf was müssen wir achten, wenn wir mit dem Taschenrechner Grad und Bogenmaß umrechnen. Taschenrechner-Modi: DEG, RAD, GRAD. Bogenmaß statt Gradmaß beim Sinus: sin(90°) = sin(0,5·Pi) = 1. Bogenmaß bei der Sinusfunktion.Zugang bestellen
-
TRI07-4 Bogenmaß - Herleitung der Kreiszahl PiWir schauen uns die Kreiszahl Pi näher an: Warum schreibt man Pi? Pi als Verhältnis von Kreisumfang/Kreisdurchmesser. Wir zeigen, wie wir uns dem Pi-Wert von 3,1415... über Polygone (Vielecke) annähern können.Zugang bestellen
-
 9 minKlasse 10TRI08-1 Trigonometrische Gleichung - EinführungEinführung zu Gleichungen und Lösungsmöglichkeiten (1 Lösung, mehrere Lösungen, keine Lösung). Was ist das Intervall und wie beeinflusst es die Lösungsmenge bei den Trigonometrischen Gleichungen. Wie ist die Lösung im Bogenmaß anzugeben.Lektion öffnen
9 minKlasse 10TRI08-1 Trigonometrische Gleichung - EinführungEinführung zu Gleichungen und Lösungsmöglichkeiten (1 Lösung, mehrere Lösungen, keine Lösung). Was ist das Intervall und wie beeinflusst es die Lösungsmenge bei den Trigonometrischen Gleichungen. Wie ist die Lösung im Bogenmaß anzugeben.Lektion öffnen -
TRI08-2 Trigonometrische Gleichung - Zweite Lösung per IdentitätDie Gleichung sin(x)=0,5 hat 2 Lösungen im Intervall [0°, 360°]. Darstellung der 2. Lösung am Einheitskreis mittels Identität sin(x) = sin(180°-x). Wir lernen den Periodizitätssummand kennen. Lösung am Sinusgraphen, Umrechnung der Lösung ins Bogenmaß.Zugang bestellen
-
TRI08-3 Trigonometrische Gleichung - cos(x)=-0,5 und sin(2·x)=0,5 lösenWir lösen die Gleichung cos(x)=-0,5. Darstellung am Einheitskreis. 2. Lösung mit Hilfe der Identität cos(x) = cos(-x). Periodizitätssummand bei Kosinus. Lösung der Aufgabe: sin(2·x)=0,5. Wie verändert der Faktor vor x die Lösung + Periode. Darstellung am Funktionsgraphen.Zugang bestellen
-
TRI08-4 Trigonometrische Gleichung - Nullstellen des SinusgraphenWir untersuchen sin(x), sin(2x), sin(x+10°), sin(x-90°) und sin(2·x-90°). Auswirkungen auf die Nullstelle des Sinusgraphen. Herleitung der allgemeinen Lösungsformel x = -c/b + k·180/b für alle Nullstellen von sin(b·x)+c = 0.Zugang bestellen
-
TRI08-5 Trigonometrische Gleichung - Lösen von SinusgleichungenNullstellen bei a·sin(b·x+c)+d=0. Lösung der Gleichung sin(2x+30°)-0,5=0. Berechnung der Periode und Ermittlung der 2. Nullstelle mittels Sinusidentität unter Berücksichtigung der veränderten Sinusgleichung.Zugang bestellen
-
TRI08-6 Trigonometrische Gleichung - KosinusgleichungenWir lösen die Kosinusgleichung cos(2x-90°)+0,5=0. Ermittlung der zweiten Lösung über Kosinusidentität.Zugang bestellen
-
TRI08-7 Trigonometrische Gleichung - TangensgleichungenWir lösen die Tangensgleichung: 0,3·tan(1,5x-90°)+0,3=0. Periode bei Tangens mit 180°/b.Zugang bestellen
-
 15 minKlasse 10,11TRI09-1 Additionstheoreme - Verständliche Herleitung für SinusIn diesem Video zeigen wir die grafische Herleitung des Additionstheorems für Sinus mit sin(α+β) = sin(α)·cos(β)+cos(α)·sin(β) sowie die Anwendung der Additionstheoreme zum Nachweis von trigonometrischen Identitäten.Lektion öffnen
15 minKlasse 10,11TRI09-1 Additionstheoreme - Verständliche Herleitung für SinusIn diesem Video zeigen wir die grafische Herleitung des Additionstheorems für Sinus mit sin(α+β) = sin(α)·cos(β)+cos(α)·sin(β) sowie die Anwendung der Additionstheoreme zum Nachweis von trigonometrischen Identitäten.Lektion öffnen -
TRI09-2 Additionstheoreme - Zum Nachweis von Sinuswerten über 90°Wir zeigen, wie das Sinus-Additionstheorem zum rechnerischen Nachweis von Sinuswerten für Winkel größer 90° genutzt werden kann.Zugang bestellen
-
TRI09-3 Additionstheoreme - Verständliche Herleitung für KosinusVollständige Herleitung des Additionstheorems für Kosinus: cos(α+β) = cos(α)·cos(β)+sin(α)·sin(β)Zugang bestellen
-
TRI09-4 Additionstheoreme - Herleitung für TangensWir zeigen, wie sich das Additionstheorem für Tangens ergibt mit: tan(α + β) = ( tan(α) + tan(β) ) / ( 1 - tan(α)·tan(β) ). Danach nutzen wir das Additionstheorem, um Tangenswerte für Winkel größer 90° zu berechnen.Zugang bestellen
-
TRI09-5 Additionstheoreme - Weitere AdditionstheoremeWas passiert, wenn wir statt sin(α + β) ein sin(α - β) haben? Es ergeben sich neue Additionstheoreme. Wir zeigen, welche das sind für sin(α - β), cos(α - β) und tan(α - β) inklusive Herleitung.Zugang bestellen
-
TRI09-6 Additionstheoreme - Herleitung DoppelwinkelfunktionenDie Doppelwinkelfunktionen sind ein Spezialfall der Additionstheoreme, hier wird der Sinus/Kosinus/Tangens vom doppelten Winkel betrachtet. Welche neuen Formeln sich ergeben, lernen wir in diesem Video. Abschließend lösen wir noch einige Aufgaben mit Hilfe der Additionstheoreme.Zugang bestellen
-
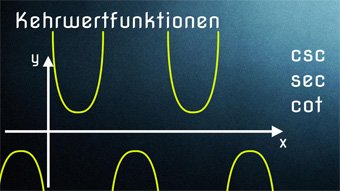
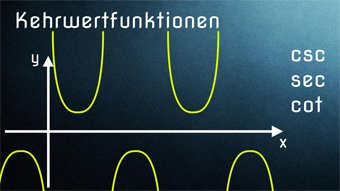
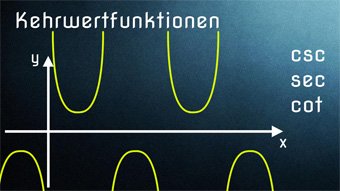
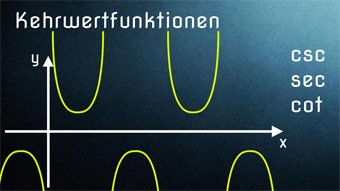
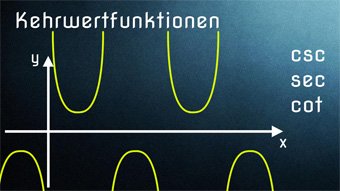
TRI10-1 Kehrwertfunktionen - EinführungWas bedeutet Kehrwert bei der Funktion. Wie sind die Kehrwertfunktionen definiert. Sinus → Kosekans, Kosinus → Sekans, Tangens → Kotangens. Wertebereich (mögliche y-Werte) der Kehrwertfunktionen.Zugang bestellen
-
TRI10-2 Kehrwertfunktionen - Kosekans u. Sekans am EinheitskreisWir betrachten uns, wie sich die Kehrwertfunktionen Kosekans und Sekans am Einheitskreis ergeben. Klärung der Begriffe Ko-Sekans und Sekans über den Sekantenabschnitt.Zugang bestellen
-
TRI10-3 Kehrwertfunktionen - Kotangens am EinheitskreisWir schauen uns an, wie Kotangens am Einheitskreis abgelesen wird und weshalb man den Begriff Ko-Tangens verwendet.Zugang bestellen
-
TRI10-4 Kehrwertfunktionen - Kosekans, Sekans, KotangensWir betrachten die Kosekansfunktion, Sekansfunktion und Kotangensfunktion inklusive Definitionslücken. Beispielaufgabe zum Finden des Schnittpunktes: cot(x-30°) = tan(x-30°).Zugang bestellen
-
TRI10-5 Ergänzungen zur TrigonometrieBerechnung der Aufgabe sin(x)=cos(x). Was sind gemischt-goniometrische Gleichungen. Blick auf die Umkehrfunktion Arkussinus. Ausdruck des Sinuswertes sin(45°) über eine Wurzel. Rückführung der trigonometrischen Funktionen auf Sinus. Ausblick höhere Mathematik: Taylorreihen + Fourierreihen.Zugang bestellen
-
 12 minKlasse 10PR01-1 Vorbereitung Matheprüfung - Aufgabenblock 1Wir bereiten uns auf die Prüfungen vor, damit ihr diese sicher besteht. Wir testen euer Wissen und lösen Aufgaben zu Prozenten, Dezimalzahlen, Dreisatz, Geometrie.Lektion öffnen
12 minKlasse 10PR01-1 Vorbereitung Matheprüfung - Aufgabenblock 1Wir bereiten uns auf die Prüfungen vor, damit ihr diese sicher besteht. Wir testen euer Wissen und lösen Aufgaben zu Prozenten, Dezimalzahlen, Dreisatz, Geometrie.Lektion öffnen -
PR01-2 Vorbereitung Matheprüfung - Aufgabenblock 2Prüfungsvorbereitung: Aufgaben zu Anteilen, Term vereinfachen, Geraden-Schnittpunkte, Gleichung lösen, Prozentwert berechnen, schriftliches Multiplizieren, Steigungswinkel berechnen, Wahrscheinlichkeit Ziehung roter Kugeln, Term bestimmen für Flächeninhalt Dreieck.Zugang bestellen
-
PR01-3 Vorbereitung Matheprüfung - Aufgabenblock 3Weiter geht es mit Prozentrechnung und Exponentialfunktionen. Wir stellen eine Funktionsgleichung auf, die die Sprunghöhe eines Balls und die Anzahl seiner Bodenkontakte in Zusammenhang bringt.Zugang bestellen
-
PR01-4 Vorbereitung Matheprüfung - Aufgabenblock 4Nun lösen wir eine Aufgabe zu einem Geländelauf, es sind Strecken an 2 Dreiecken zu berechnen. Wir verwenden den Innenwinkelsummensatz, den Satz des Pythagoras, Kosinus und Sinussatz.Zugang bestellen
-
PR01-5 Vorbereitung Matheprüfung - Aufgabenblock 5Wir lösen eine Aufgabe aus dem Alltag. Die Wohnungsmiete inkl. Nebenkosten soll nach Zimmerflächen aufgeteilt werden. Zusätzlich Flächenberechnung inkl. Sinus-Anwendung und Winkelbestimmung. Abschließende Aufgabe mit Zinseszins.Zugang bestellen
-
PR01-6 Vorbereitung Matheprüfung - Aufgabenblock 6Wir lösen Aufgaben mit Volumen (Stein im Wasser), berechnen Kegelvolumen (Kerzen) und ermitteln das Volumen der Cheops-Pyramide.Zugang bestellen
-
PR01-7 Vorbereitung Matheprüfung - Aufgabenblock 7Aufgaben zu Funktionen: Parabel mit Parameter und gegebenem Punkt, Scheitelpunktform aus Allgemeinform bestimmen, Geradengleichung aus 2 Punkten bestimmen.Zugang bestellen
-
PR01-8 Vorbereitung Matheprüfung - Aufgabenblock 8Wahrscheinlichkeit mindestens eine 6 beim Wurf von zwei Würfeln zu erzielen. Und Wahrscheinlichkeit, die Augensumme 6 zu werfen. Gewinnspiel mit Einsatz und Gewinn - Erwartungswert berechnen.Zugang bestellen
-
PR01-9 Vorbereitung Matheprüfung - Aufgabenblock 9Anwendungsaufgaben Maße, Volumen, Funktionen. Golfbälle in Schachtel, Volumenanteil prozentual bestimmen, Flugbahn Golfball bestimmen anhand quadratischer Funktion (Parabel).Zugang bestellen
-
 10 minKlasse 10PR02-1 Berlin 2008 - Werte ordnen, Brüche, PotenzenAufgabe 1a: Werte von Potenz, Wurzel, Bruch zu Kommazahlen umwandeln und der Größe nach sortieren, Aufgabe 1b: Brüche umformen und berechnen, Aufgabe 1c: Potenzen im BruchtermLektion öffnen
10 minKlasse 10PR02-1 Berlin 2008 - Werte ordnen, Brüche, PotenzenAufgabe 1a: Werte von Potenz, Wurzel, Bruch zu Kommazahlen umwandeln und der Größe nach sortieren, Aufgabe 1b: Brüche umformen und berechnen, Aufgabe 1c: Potenzen im BruchtermLektion öffnen -
PR02-2 Berlin 2008 - Formel aus Textaufgabe, MaßstäbeAufgabe 1d: Formel aus Textaufgabe aufstellen und lösen, Aufgabe 1e: Maßstäbe berechnen und Längen umwandeln.Zugang bestellen
-
PR02-3 Berlin 2008 - Sinus, Kosinus, ArkustangensAufgabe 2: Anwendung von Sinus, Kosinus und Arkustangens (tan^(-1)) zur Berechnung von Winkeln und Seiten eines DreiecksZugang bestellen
-
PR02-4 Berlin 2008 - Wahrscheinlichkeit bei LosenAufgabe 3: Anwendung der Wahrscheinlichkeit beim Ziehen von Losen (Gewinne vs. Nieten).Zugang bestellen
-
PR02-5 Berlin 2008 - Anwendung des TangensAufgabe 4: Anfertigen einer Skizze + Anwendung des Tangens bei einer Sachaufgabe zur Ermittlung einer Strecke (Tourist fotografiert Brandenburger Tor).Zugang bestellen
-
PR02-6 Berlin 2008 - Volumen, Radius, OberflächeAufgabe 5: Aufgabe zur Volumen-Berechnung von Kugel und Würfel, Radius und Durchmesser, Kugeloberfläche (Preis je m²).Zugang bestellen
-
PR02-7 Berlin 2008 - Zuordnungen, PreisnachlassAufgabe 6: Zuordnungen am Beispiel von Kajaks und Canadiern, Preisliste nutzen, Übersicht bewahren, am Ende Preis-Nachlass von 10 % Prozent berechnen.Zugang bestellen
-
PR02-8 Berlin 2008 - Aussagen prüfen, Gleichung prüfenAufgabe 7: Aussagen auf Richtigkeit prüfen (Logik), Aufgabe 8: Gleichung mit Unbekannten umformen und auflösen.Zugang bestellen
-
PR02-9 Berlin 2008 - Diagramme, Graphen-SchnittpunktAufgabe 9: Diagramme deuten (Entfernung-Zeit-Diagramm), Aufgabe 10: Deuten von Funktionen, Gleichung von Funktionen aufstellen, Schnittpunkt von 2 Graphen finden, Vorgehen erklärenZugang bestellen
-
 12 minKlasse 7,8VEK01-1 Einführung Vektoren - Geom. Verschiebung berechnenWas bedeutet Vektor, geometrische Verschiebung in der Ebene mit Vektoren exakt berechnen, Komponenten des Vektors, Vektor als Pfeile mit bestimmter Länge und bestimmter Richtung, Vektornotation, Repräsentanten des Vektors.Lektion öffnen
12 minKlasse 7,8VEK01-1 Einführung Vektoren - Geom. Verschiebung berechnenWas bedeutet Vektor, geometrische Verschiebung in der Ebene mit Vektoren exakt berechnen, Komponenten des Vektors, Vektor als Pfeile mit bestimmter Länge und bestimmter Richtung, Vektornotation, Repräsentanten des Vektors.Lektion öffnen -
VEK01-2 Einführung Vektoren - Definition und AnwendungsbeispieleWas ist ein Vektor? Definition geometrisch und als Zahlenpaar. Schreibweisen für Vektoren. Geschwindigkeit als Anwendungsbeispiele für Vektoren: Gleichförmige Bewegung, kreisförmige Bewegung, Bewegung mit Verzögerung. Übungen zur Gleichheit von Vektoren.Zugang bestellen
-
VEK02-1 Vektoren bestimmen - Verbindungsvektor, OrtsvektorWir bestimmen einen Vektor (seine Komponenten x und y) aus den Koordinaten zweier Punkte. Wir lernen die Begriffe Verbindungsvektor, Ortsvektor und Verschiebungsvektor kennen.Zugang bestellen
-
VEK02-2 Vektoren bestimmen - Vektorlänge, NullvektorDie Länge eines Vektors (auch Vektorbetrag genannt) kann mit Hilfe vom Satz des Pythagoras berechnet werden. Hierzu ziehen wir die Wurzel aus den Komponenten x² plus y². Wenn ein Vektor die Länge Null hat, sprechen wir vom Nullvektor.Zugang bestellen
-
VEK03-1 Vektoraddition - Addition von Orts- und VerschiebungsvektorEinführung der Addition über Ortsvektoren und Verschiebungsvektoren. Komponentenweise Addition. Geometrische Darstellung für Ortsvektor a + Verschiebungsvektor v = Ortsvektor bZugang bestellen
-
VEK03-2 Vektoraddition - Addition von 2 OrtsvektorenWie addiert man zwei Ortsvektoren. Regel für die geometrische Darstellung: Verschiebung der Vektoren (Anfangspunkt auf Endpunkt, Spitze-Fuß-Regel). Kommutativgesetz für Vektoren a + b = b + a. Resultierender Vektor als kürzeste Verbindung (Vektorbeträge).Zugang bestellen
-
VEK03-3 Vektoraddition - Addition mehrerer VektorenWie addiert man mehrere Vektoren miteinander. Die Komponenten aller Vektoren müssen addiert werden. Schrittweise geometrische Darstellung der Vektoraddition auf der Ebene.Zugang bestellen
-
VEK03-4 Vektoraddition - Beispiel zur Addition, Nullvektor, VektorketteGeometrisches Beispiel einer Vektoraddition, Verschiebung der Vektoren aufeinander, Kommutativgesetz geometrisch, Nullvektor bei der Addition, geschlossene Vektorkette, Darstellung der Komponenten eines Vektors als Vektoren.Zugang bestellen
-
VEK04-1 Vektorsubtraktion - Einführung GegenvektorVektorsubtraktion mit dem Gegenvektor. Vektor a - Vektor b als Vektor a + Gegenvektor b. Geometrische Deutung der Subtraktion bei Ortsvektoren. Reihenfolge der Subtraktion entscheidet über die Richtung des resultierenden Vektors. Subtraktion von Verschiebungsvektoren.Zugang bestellen
-
VEK04-2 Vektorsubtraktion - Umfang eines Dreiecks ermittelnDie gegebenen Dreieckspunkte werden als Ortsvektoren interpretiert, danach subtrahieren wir die Ortsvektoren, um die Vektoren zwischen ihnen zu erschaffen. Anschließend erhalten wir mittels der Vektorlängen den Dreiecksumfang. Rechnerisch und geometrische Darstellung.Zugang bestellen
-
 8 minKlasse 7,8VEK05-1 Skalarmultiplikation - Einführung Skalar mal VektorWas ist ein Skalar (Zahl), wie multiplizieren wir einen Skalar mit einem Vektor s·v=r, was bedeutet das geometrisch. Vektorlängen entsprechend des Skalars (Vektorstreckung, Vektorstauchung). Gegenvektor mit (-1)·v.Lektion öffnen
8 minKlasse 7,8VEK05-1 Skalarmultiplikation - Einführung Skalar mal VektorWas ist ein Skalar (Zahl), wie multiplizieren wir einen Skalar mit einem Vektor s·v=r, was bedeutet das geometrisch. Vektorlängen entsprechend des Skalars (Vektorstreckung, Vektorstauchung). Gegenvektor mit (-1)·v.Lektion öffnen -
VEK05-2 Skalarmultiplikation - RechengesetzeKommutativgesetz, Assoziativgesetz und Distributivgesetz für die Skalarmultiplikation. Geometrische Darstellung des Distributivgesetzes s·(a+b) = s·a + s·b für die Skalarmultiplikation.Zugang bestellen
-
VEK06-1 EinheitsvektorWas ist der Einheitsvektor und wie berechnen wir seine Komponenten. Was sind Basisvektoren.Zugang bestellen
-
 9 minKlasse 11,12DIF01-1 Grenzwerte - Einführung LimesWas ist ein Grenzwert / Limes. Wann schreibt man lim. Was ist eine Asymptote. Grenzwerte für x gegen unendlich und x gegen Null. Rechtsseitiger und Linksseitiger Grenzwert.Lektion öffnen
9 minKlasse 11,12DIF01-1 Grenzwerte - Einführung LimesWas ist ein Grenzwert / Limes. Wann schreibt man lim. Was ist eine Asymptote. Grenzwerte für x gegen unendlich und x gegen Null. Rechtsseitiger und Linksseitiger Grenzwert.Lektion öffnen -
DIF01-2 Grenzwerte - Regeln und GrenzwertsätzeRegel lim 1/x = 0 zum Ermitteln von Limeswerten für Funktionen. Grenzwertsätze zum Berechnen des Limes. Grenzwerte an einer Stelle.Zugang bestellen
-
DIF01-3 Grenzwerte - ÜbungsaufgabenVerschiedene Übungsaufgaben zur Limesberechnung. Limes richtig berechnen und korrekt notieren. 3 Fälle bei Grenzwertberechnungen beim Vergleich von Zählergrad und Nennergrad der gebrochenrationalen Funktionen.Zugang bestellen
-
DIF01-4 Grenzwerte - Definition / ErklärungFür Fortgeschrittene: Wir erklären, wie Grenzwerte mathematisch über eine Umgebung definiert sind. Zusätzlich lernen wir "konvergiert" und "divergiert" kennen.Zugang bestellen
-
 12 minKlasse 11,12DIF02-1 Grafisches Ableiten (Einführung zur Ableitung)Was ist ein Ableitung und wie kann man einen Graphen grafisch ableiten. Was ist die Steigung in einem Punkt und was hat eine Tangente bzw. Steigungstangente damit zu tun. Wir erstellen grafisch die Ableitungsfunktion am Beispiel der quadratischen Funktion. Auch lernen wir Hochpunkte und Tiefpunkte kennen.Lektion öffnen
12 minKlasse 11,12DIF02-1 Grafisches Ableiten (Einführung zur Ableitung)Was ist ein Ableitung und wie kann man einen Graphen grafisch ableiten. Was ist die Steigung in einem Punkt und was hat eine Tangente bzw. Steigungstangente damit zu tun. Wir erstellen grafisch die Ableitungsfunktion am Beispiel der quadratischen Funktion. Auch lernen wir Hochpunkte und Tiefpunkte kennen.Lektion öffnen -
DIF02-2 Grafisches Ableiten (Beispiele)Wie werden die Graphen von kubischen Funktionen grafisch abgeleitet. Wie werden Sinus- und Kosinusfunktion grafisch abgeleitet.Zugang bestellen
-
 7 minKlasse 11,12DIF03-1 Differentialrechnung - Voraussetzungen zum VerstehenNötige Voraussetzungen zum Einstieg in die Differentialrechnung: Lineare Funktionen, Grenzwert (Limes), grafisches Ableiten. Wir lernen den Differenzenquotienten kennen.Lektion öffnen
7 minKlasse 11,12DIF03-1 Differentialrechnung - Voraussetzungen zum VerstehenNötige Voraussetzungen zum Einstieg in die Differentialrechnung: Lineare Funktionen, Grenzwert (Limes), grafisches Ableiten. Wir lernen den Differenzenquotienten kennen.Lektion öffnen -
DIF03-2 Differentialrechnung - Funktion rechnerisch ableitenWas ist die Differentialrechnung. Vom Differenzenquotient zum Differentialquotient. Wie wird mit Differentialquotient die rechnerische Ableitung gebildet. Hilfsmittel Limes.Zugang bestellen
-
DIF03-3 Differentialrechnung - h-MethodeMit Hilfe einer Ableitungsfunktion kann man die Steigung an einer Stelle sofort berechnen. Mit der h-Methode können wir diese Funktionsgleichung ermitteln.Zugang bestellen
-
DIF03-4 Differentialrechnung - AbleitungsregelnWir lernen die wichtigen Ableitungsregeln kennen: Potenzregel mit f(x)=x^n zu f`(x)=n·x^(n-1) sowie Faktorregel und konstante Funktion. Hinweise zur E-Funktion und deren Ableitung. Ableitung von Sinus und Kosinus.Zugang bestellen
-
DIF03-5 Differentialrechnung - AbleitungsregelnWir lernen die Ableitungsregeln kennen: Potenzregel, konstante Funktion, Faktorregel, Summenregel, Produktregel, Quotientenregel, Kettenregel. Inkl. Beispielrechnungen.Zugang bestellen
-
VID29-7 Entstehung der ZahlenAus welchen Gründen sind Zahlen (bzw. Zahlzeichen) entstanden? Wir blicken auf die Geschichte der Zahlen und erklären ihren Zweck sowie die Vorteile der heute verwendeten Zehnerzahlen.Zugang bestellen
-
VID29-8 Mengen abzählenWir zählen Mengen an Beispielen ab und benutzen die Zahlzeichen (Zahlen), um die Anzahl der Dinge (Elemente) anzugeben. Auch betrachten wir Teilmengen und gemischte Mengen.Zugang bestellen
-
VID29-9 Mengen festlegenWir legen Mengen selbst fest anhand von Beispielen. Zudem bilden wir beliebige Teilnmenge aus einer Menge an Spielsteinen.Zugang bestellen
-
VID30-0 Natürliche ZahlenEinführung zu der Menge der natürliche Zahlen. Vom Zählen mit Fingern zu den Zahlzeichen. Nachfolger einer Zahl. Unendlich viele Zahlen. Mengenschreibweise.Zugang bestellen
-
VID30-1 StellenwerttafelEinführung der Stellenwerttafel. Unterschied zwischen Ziffern und Zahlen. Was ist eine Stelle und ein Stellenwert. Wie sieht die Stellenwerttafel aus?Zugang bestellen
-
VID30-2 Zahlen in Stellenwerttafel eintragenMit einer Stellenwerttafel erkennen wir schnell, welche Ziffer an welcher Stelle steht und welchen Wert diese Stelle hat. Wir erstellen Stellenwerttafeln und tragen Zahlen ein.Zugang bestellen
-
VID30-3 Zahlen aus Stellenwerttafel ablesenWir üben das Lesen von großen Zahlen (Millionen, Millarde) mit der Stellenwerttafel. Wir lesen die Stellen ab und deren Werte.Zugang bestellen
-
VID30-4 StellenwertsystemWir erklären ein Stellenwertsystem: Ein System, bei dem die Stelle einer Ziffer innerhalb einer Zahl ihren Wert angibt. Zudem stellen wir Stellenwerte grafisch dar.Zugang bestellen
-
VID30-5 Zahlen bis BillionenWir behandeln die Namen (Zahlwörter) für große Zahlen bis Billionen. Also Tausend, Million, Millarde, Billion. Wir zeigen an Beispielen, wie man sie richtig vorliest.Zugang bestellen
-
VID30-6 ZahlenstrahlWir lernen den Aufbau vom Zahlenstrahl kennen. Mit Startwert und Einheitsstrecke (gleiche Abstände). Wir erstellen einen Zahlenstrahl.Zugang bestellen
-
VID30-7 Natürliche Zahlen am ZahlenstrahlWir zeichnen einen Zahlenstrahl und tragen natürliche Zahlen ab. Wir nehmen einen beliebigen Startwert und legen die Anzahl an Abständen fest. Dann berechnen wir die Einheitsstrecke.Zugang bestellen
-
VID30-8 Vorgänger und Nachfolger bei natürlichen ZahlenWir schauen uns Vorgänger und Nachfolger bei natürlichen Zahlen an. Auch behandeln wir den Vorgänger der 0, die -1 (negative Zahl).Zugang bestellen
-
VID30-9 Natürliche Zahlen vergleichenWir vergleichen natürliche Zahlen mit Zahlenwerten und am Zahlenstrahl. Wir lernen die Vergleichszeichen kennen: „größer als“, „kleiner als“ und „gleich groß wie“.Zugang bestellen
-
VID31-0 TeilbarkeitWir erklären, was Teilbarkeit bedeutet und wann eine Zahl durch eine andere Zahl teilbar ist, und wann die Zahl nicht teilbar ist. Wir benutzen die Divison mit Rest.Zugang bestellen
-
VID31-1 Teilbarkeit durch 2Wir erklären die Regel zur Teilbarkeit durch 2 und zeigen mehrere Beispiele, in welchen Fällen durch 2 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-2 Teilbarkeit durch 3Wir erklären die Regel zur Teilbarkeit durch 3 (Quersumme) und zeigen mehrere Beispiele, in welchen Fällen durch 3 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-3 Teilbarkeit durch 5Wir erklären die Regel zur Teilbarkeit durch 5 und zeigen mehrere Beispiele, in welchen Fällen durch 5 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-4 Teilbarkeit durch 10Wir erklären die Regel zur Teilbarkeit durch 10 und zeigen mehrere Beispiele, in welchen Fällen durch 10 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-5 Teilbarkeit durch 6Wir erklären die Regel zur Teilbarkeit durch 6 und zeigen mehrere Beispiele, in welchen Fällen durch 6 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-6 Teilbarkeit durch 9Wir erklären die Regel zur Teilbarkeit durch 9 (Quersumme) und zeigen mehrere Beispiele, in welchen Fällen durch 9 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-7 Teilbarkeit durch 4Wir erklären die Regel zur Teilbarkeit durch 4 und zeigen mehrere Beispiele, in welchen Fällen durch 4 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-8 Teilbarkeit durch 7Wir erklären die Regel zur Teilbarkeit durch 7 und zeigen mehrere Beispiele, in welchen Fällen durch 7 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID31-9 Teilbarkeit durch 8Wir erklären die Regel zur Teilbarkeit durch 8 und zeigen mehrere Beispiele, in welchen Fällen durch 8 teilbar bzw. nicht teilbar ist.Zugang bestellen
-
VID32-0 PrimzahlenWir lernen Primzahlen und zusammengesetzte Zahlen kennen. Wir betrachten Zahlen von 1 bis 20. Gerade und ungerade Primzahlen. Beispiele.Zugang bestellen
-
VID32-1 Primzahlen ermittelnZum Ermitteln von Primzahlen betrachten wir die Methode namens Sieb des Eratosthenes. Hierbei werden alle Vielfachen einer Primzahl weggestrichen.Zugang bestellen
-
VID32-2 PrimfaktorzerlegungBei der Primfaktorzerlegung wird eine natürliche Zahl als Multiplikation von Primzahlen geschrieben. Wir betrachten einige Beispiele.Zugang bestellen
-
VID32-3 Runden von natürlichen ZahlenEinführung zum Runden von Zahlen. Was sind Abrunden und Aufrunden. Rundungsregeln. Runden im Alltag. Beispiele zum Runden. Runden auf Zehnerstelle, Hunderterstelle und Tausenderstelle.Zugang bestellen
-
VID32-4 Natürliche Zahlen sinnvoll rundenBeim „sinnvollen“ Runden darf die Zahl angepasst werden, sodass sie leichter zu merken ist. Beim „unsinnigen“ Runden kommt es stets auf die genaue Zahl an.Zugang bestellen
-
VID32-5 Natürliche Zahlen im AlltagDie natürlichen Zahlen finden sich überall im Alltag wieder. Wir nennen verschiedene Beispiele (Zählen, Maßangaben, Daten erfassen).Zugang bestellen
-
VID32-6 Römische Zahlen (Einführung)Einführung der römischen Zahlzeichen I, V, X, L, C, D, M. Historische Herkunft der Zahlzeichen. Beispiele römischer Zahlen.Zugang bestellen
-
VID32-7 Regeln bei römischen ZahlenWir lernen die Regeln bei römischen Zahlen kennen: Additionsregel, Maximal 3 gleiche Zeichen, Subtraktionsregel, Reihenfolge bei Subtraktion.Zugang bestellen
-
VID32-8 Beispiele von römischen ZahlenWir zeigen an Beispielen, wie wir Dezimalzahlen in römische Zahlen umwandeln können.Zugang bestellen
-
VID32-9 BinärzahlenAufbau von Binärzahlen (Zweierzahlen) mit Ziffern 0 und 1. Abzählen von Binärzahlen. Dezimalwert einer Binärzahl. Stellensystem von Binärzahlen. Geschichte der Binärzahlen.Zugang bestellen
-
VID33-0 Binärzahlen in Dezimalzahlen umwandelnVorgehen zur Umwandlung einer Binärzahl in eine Dezimalzahl. Anhand von mehreren Beispielen gezeigt.Zugang bestellen
-
VID33-1 Dezimalzahlen in Binärzahlen umwandelnVorgehen zur Umwandlung einer Dezimalzahl in eine Binärzahl. Anhand von mehreren Beispielen gezeigt.Zugang bestellen
-
VID33-2 HexadezimalzahlenEinführung zu den Hexadezimalzahlen. Ziffern 0 bis 9 sowie A bis F. Stellenwerte und Schreibweise. Geschichte der Hexadezimalzahlen sowie Vorteile.Zugang bestellen
-
VID33-3 Hexadezimalzahlen in Dezimalzahlen umwandelnVorgehen zum Umwandeln von Hexadezimalzahlen in Dezimalzahlen. Stellenwerte.Zugang bestellen
-
VID33-4 Hexadezimalzahlen in Dezimalzahlen umwandelnVorgehen zum Umwandeln von Dezimalzahlen in Hexadezimalzahlen. Zerlegen der Dezimalzahl in eine Summe von Sechzehnerpotenzen.Zugang bestellen
-
VID33-5 Zahlensysteme im VergleichWir vergleichen Dezimalzahlen, Binärzahlen und Hexadezimalzahlen und zeigen Vorteile und Nachteile der Zahlensysteme auf.Zugang bestellen
-
 11 minKlasse 9VID68- Funktionen erkennen (mit Mathematik-Spiel)Hier wird erklärt, wie ihr gezeichnete Funktionsgraphen richtig erkennen könnt. Wir behandeln: Konstante Funktionen, Lineare Funktionen, Quadratische Funktionen und Kubische Funktionen.Lektion öffnen
11 minKlasse 9VID68- Funktionen erkennen (mit Mathematik-Spiel)Hier wird erklärt, wie ihr gezeichnete Funktionsgraphen richtig erkennen könnt. Wir behandeln: Konstante Funktionen, Lineare Funktionen, Quadratische Funktionen und Kubische Funktionen.Lektion öffnen -
Tutorial - Wie lernt man mit Matheretter?Dies ist ein Tutorial wie ihr am Besten Mathematik mit uns lernt. Hierzu stehen euch Videos, Programme, Aufgaben und Formelsammlung zur Verfügung. Mathe lernen wird echt einfach, wenn ihr diese Tipps befolgt.Lektion öffnen
-
Interview - Kein Bock auf Mathe in der Schule, danach MathestudentThilo (27) hatte in der Schule keine Lust auf Mathe, danach hat sich alles geändert. Warum und was ihn dazu bewegt hat, erfahrt ihr in diesem inspirierenden Video.Lektion öffnen
-
 3 minKlasse 10Warum existiert Mathematik?Ein kleiner Ausflug, um die Frage nach der Existenz der Mathematik zu beantworten.Lektion öffnen
3 minKlasse 10Warum existiert Mathematik?Ein kleiner Ausflug, um die Frage nach der Existenz der Mathematik zu beantworten.Lektion öffnen -
 7 minKlasse 11,12Zehn der beeindruckendsten Formeln der Mathematik1. Eulersche Identität 2. Euler-Produkt 3. Gaußsche Fehlerintegral 4. Mächtigkeit des Kontinuums 5. Analytische Fortsetzung der Fakultät 6. Satz des Pythagoras 7. Formel für die Fibonacci-Folge 8. Basler Problem 9. Harmonische Reihe 10. Formel für die PrimzahlzählfunktionLektion öffnen
7 minKlasse 11,12Zehn der beeindruckendsten Formeln der Mathematik1. Eulersche Identität 2. Euler-Produkt 3. Gaußsche Fehlerintegral 4. Mächtigkeit des Kontinuums 5. Analytische Fortsetzung der Fakultät 6. Satz des Pythagoras 7. Formel für die Fibonacci-Folge 8. Basler Problem 9. Harmonische Reihe 10. Formel für die PrimzahlzählfunktionLektion öffnen -
Was ist LaTeX? Vorteile von LaTeX. Einführung für AnfängerEine Einführung in LaTeX: Was ist LaTeX. Warum LaTeX verwenden? Die Vorteile von TeX. Wie kann man TeX eingeben. LaTeX-Tutorial einfach.Lektion öffnen
-
Die Zahlen von 0 bis 1000 - Ein ZählexperimentDie Zahlen von 0 bis 1000 werden in diesem Video vorgezählt, und zwar mit Anzeige des Zahlennamens ausgeschrieben, Dezimalzahl, Binärzahl, Oktalzahl, Hexadezimalzahl, als Römische Zahl, mit Primfaktoren, un/gerade Zahl.Lektion öffnen
-
Geoknecht 3D: Einführung und TutorialMit diesem Programm könnt ihr geometrische Körper einfach mit Text erstellen. Zeichenobjekte: Dreieck, Ebene, Gerade, Kugel, Polygon, Punkt, Quader, Spat, Strecke, Text, Vektor, Viereck, Würfel, Zylinder. Ihr könnt Objekte erstellen, animieren, rotieren, einfärben, Variablen festlegen.Lektion öffnen
-
Info: Verwendung von Master-AccountsInformationen zur Verwendung von Master-Accounts für Schulen. Lehrer- und Schüler-Account erstellen.Lektion öffnen
-
Info: Verwendung des KompetenzrastersWir zeigen, wie Schüler und Lehrer das Kompetenzraster verwenden können.Lektion öffnen
→ Kein Ergebnis, hast du dich vertippt?