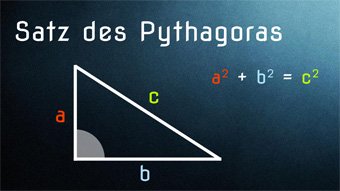
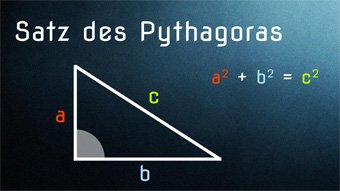
Lektion GEO04: Satz des Pythagoras

Wir wissen, was rechtwinklige Dreiecke sind und schauen uns nun den wichtigen Satz des Pythagoras an.

• 
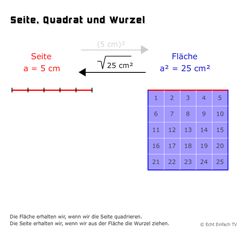  Seite, Quadrat und Wurzel

  Legt eine Seite fest und ihr Quadrat wird als Fläche angezeigt. Mit Hilfe der Wurzel kommt ihr wieder zurück zur Seitenlänge.
• 
  Rechtwinklige Dreiecke: Ähnlichkeit

  Teilt die Höhe das rechtwinklige Dreiecke in zwei Teildreiecke, so sind alle Dreiecke zueinander ähnlich. Vergrößert, verkleinert, dreht und spiegelt die Dreiecke, um dies selbst festzustellen!
• 
  Satz des Pythagoras: Prinzip verallgemeinert

  Dieses Programm veranschaulicht das Prinzip hinter dem Satz des Pythagoras. Die Flächen über den Dreiecken sind hier als Dreiecke gezeichnet, könnten aber auch andere Formen einnehmen.
• 
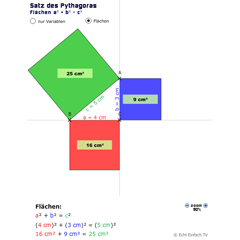  Satz des Pythagoras: Flächendarstellung

  Der Satz des Pythagoras in der am Häufigsten anzutreffenden Form dargestellt, bei der die Quadrate auf den Dreiecksseiten liegen.
• 
  Satz des Pythagoras: Nachweis

  Nachweis vom Satz des Pythagoras über das große Quadrat (a+b)², von dem 4 Dreiecksflächen abgezogen werden. Eigene Werte können eingegeben werden!
• 
  Satz des Pythagoras: Geometrischer Nachweis I

  Zwei geometrische Nachweise für den Satz des Pythagoras. Verschieben wir die Dreiecke, so erhalten wir zum einen c² und zum anderen a² und b².
• 
  Satz des Pythagoras: Geometrischer Nachweis II

  Ein weiterer geometrischer Nachweis für den Satz des Pythagoras, bei dem zwei Dreiecksflächen aus a² und b² heraus verschoben werden, die dann c² ergeben.
• 
  Satz des Pythagoras und 1. Binomische Formel

  Bei der 1. Binomischen Formel erhalten wir a² + 2·ab + b². Für die gleiche Fläche erhalten wir bei anderer Dreiecksanordnung: c² + 2·ab. Daraus ergibt sich a² + b² = c²
• 
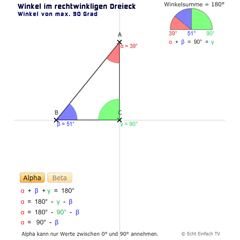  Rechtwinklige Dreiecke: Winkel max. 90 Grad

  Dieses Programm veranschaulicht, dass die Winkel in einem rechtwinkligen Dreieck nie größer als 90 Grad sein können.
• 
  Dreiecksrechner für rechtwinklige Dreiecke

  Berechnungen am rechtwinkligen Dreieck. Einfach Seite, Winkel, Höhe, p, q eingeben und das gesamte Dreieck mit fehlenden Angaben wird sofort berechnet.
• 
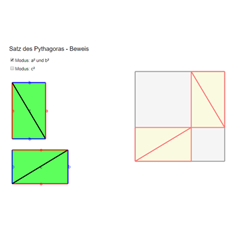  Satz des Pythagoras: Geometrischer Beweis

  Geometrischer Nachweis: Bei der 1. Binomischen Formel erhalten wir a² + 2·ab + b². Für die gleiche Fläche erhalten wir bei anderer Dreiecksanordnung: c² + 2·ab. Daraus ergibt sich a² + b² = c²

Zugriff auf alle Programme

Hier findest du 24 Arbeitsblätter, mit denen du dein Wissen testen kannst.

Hier findest du 8 Lernchecks, mit denen du dein Wissen testen kannst.

Häufige Fragen:

• Dreiecksseiten berechnen: Seite ist doppelt so lang wie die kürzeste...
• Gleichseitiges Dreieck: Seiten mit Hilfe des Flächeninhaltes berechnen
• Welche Länge können Grundlinie und Höhe eines Dreiecks mit 36cm² haben?
• Satz des Pythagoras oder Kathetensatz b² = c · q?
• Gleichungen aufstellen: Dreimal so alt wie sein Sohn + Seite des Dreiecks 10 cm länger
• Ein Giebelfenster soll verglast werden. Wie groß ist die Scheibe?
• Welche linearen Funktionen haben diese Dreiecksseiten als Graph?

Finde weitere Fragen und Antworten in der Mathelounge.