AB: Satz des Pythagoras - Einführung/Beweis

Mit Hilfe vom Satz des Pythagoras kann man bei einem rechtwinkligen Dreieck die unbekannte Dreiecksseite ausrechnen, wenn 2 Dreiecksseiten bekannt sind. Hierzu nutzt man Flächen (Quadrate), um einen Zusammenhang zwischen den Dreiecksseiten herzustellen. Der Satz des Pythagoras lässt sich wie folgt herleiten:

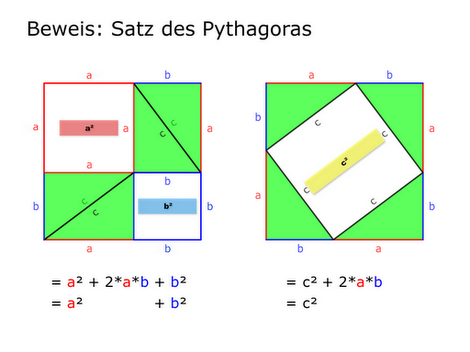
Wir sehen, dass das große Quadrat die Seitenlänge (a + b) hat und damit die Fläche (a + b)². Nun können wir das linke große Quadrat zerlegen in die Flächen: Quadrat a², Quadrat b² und 4 gefärbte Dreiecke. Die Formel lautet: (a + b)² = a² + b² + 4·\( \frac{a·b}{2} \). Das rechte Quadrat können wir zerlegen in die Flächen: Quadrat c² und 4 gefärbte Dreiecke. Die Formel lautet (a + b)² = c² + 4·\( \frac{a·b}{2} \).

Nun stellen wir die Formeln auf:
(a + b)² = a² + b² + 4·\( \frac{a·b}{2} \)   sowie   (a + b)² = c² + 4·\( \frac{a·b}{2} \)

Stellen wir beide Gleichungen gegenüber:
(a + b)² = (a + b)²
a² + b² + 4·\( \frac{a·b}{2} \) = c² + 4·\( \frac{a·b}{2} \)

Und formen wir um, indem wir 4·\( \frac{a·b}{2} \) auf beiden Seiten subtrahieren, es bleibt stehen:
a² + b² = c²

Das ist der Satz des Pythagoras.

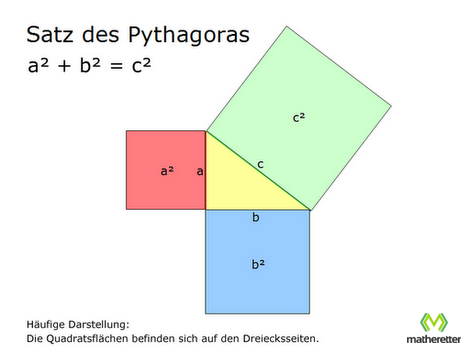
Mit dieser Formel lassen sich nun Seiten von rechtwinkligen Dreiecken leicht berechnen. Ein Beispiel: Wir haben ein rechtwinkliges Dreieck mit den Seiten a = 5 cm und b = 8 cm. Wie lang ist nun die längste Seite c? (Man nennt die längste Seite Hypotenuse und die beiden kürzeren Katheten.)

$$ a^2 + b^2 = c^2 \\ c = \sqrt{a^2 + b^2} \quad | \; a = 5 \;cm \text{ und } b = 8 \;cm \\ c = \sqrt{(5 \;cm)^2 + (8 \;cm)^2} \\ c = \sqrt{25 \;cm^2 + 64 \;cm^2} \\ c = \sqrt{89 \;cm^2} ≈ 9,43 \;cm $$