AB: Dreiecksseiten mit Pythagoras berechnen
Mit dem Satz des Pythagoras lassen sich alle Seiten eines rechtwinkligen Dreiecks bestimmen, sofern zwei Seiten gegeben sind und wir wissen, welche die längste Seite (die Hypotenuse) ist. Im Folgenden ein paar Rechenaufgaben, mit denen ihr euer Wissen testen könnt. Bitte schreibt euren kompletten Lösungsweg auf, um eventuelle Fehler nachvollziehen zu können.
Benutze den Satz des Pythagoras, um die jeweils fehlende Seite des rechtwinkligen Dreiecks zu berechnen.
Seite c = 5 cm
Der rechte Winkel ist γ, damit ist die längste Seite die ihm gegenüberliegende Seite c.
\( a^2 + b^2 = c^2 \\ c = \sqrt{a^2 + b^2} \\ c = \sqrt{(3\;cm)^2 + (4\;cm)^2} \\ c = \sqrt{25\;cm^2} \\ c = 5\;cm \)
Seite c ≈ 2,646 cm
Der rechte Winkel ist β, damit ist die längste Seite die ihm gegenüberliegende Seite b.
\( a^2 + c^2 = b^2 \\ c^2 = b^2 - a^2 \\ c = \sqrt{b^2 - a^2} \\ c = \sqrt{(4\;cm)^2 - (3\;cm)^2} \\ c = \sqrt{7\;cm^2} \\ c ≈ 2,646\;cm \)
Seite a ≈ 11,402 cm
Der rechte Winkel ist α, damit ist die längste Seite die ihm gegenüberliegende Seite a.
\( b^2 + c^2 = a^2 \\ a = \sqrt{b^2 + c^2} \\ a = \sqrt{(9\;cm)^2 + (7\;cm)^2} \\ a = \sqrt{7\;cm^2} \\ a ≈ 11,402\;cm \)
Seite b ≈ 11,314 cm
Der rechte Winkel ist α, damit ist die längste Seite die ihm gegenüberliegende Seite a.
\( b^2 + c^2 = a^2 \\ b = \sqrt{a^2 - c^2} \\ b = \sqrt{(12\;cm)^2 - (4\;cm)^2} \\ b = \sqrt{128\;cm^2} \\ b ≈ 11,314\;cm \)
Seite c ≈ 11,737 m
Der rechte Winkel ist β, damit ist die längste Seite die ihm gegenüberliegende Seite b.
\( a^2 + c^2 = b^2 \\ c = \sqrt{b^2 - a^2} \\ c = \sqrt{(12\;m)^2 - (2,5\;m)^2} \\ c = \sqrt{137,75\;m^2} \\ c ≈ 11,737\;m \)
Seite b ≈ 3,437 km
Der rechte Winkel ist γ, damit ist die längste Seite die ihm gegenüberliegende Seite c.
\( a^2 + b^2 = c^2 \\ b = \sqrt{c^2 - a^2} \\ b = \sqrt{(4250\;m)^2 - (2500\;m)^2} \\ b = \sqrt{11812500\;m^2} \\ b ≈ 3436,932\;m ≈ 3,437\;km \)
Benutze den Winkelsummensatz für Dreiecke sowie den Satz des Pythagoras, um die fehlenden Seiten und Winkel der rechtwinkligen Dreiecke zu berechnen.
Winkel β =
Seite c = 8 cm
Winkel β = 48,59°
Bestimmen wir den fehlenden Winkel:
β = 180° - α - γ = 180° - 41,41° - 90° = 48,59°
β = 48,59°
Bestimmen wir die fehlende Seite (γ ist rechter Winkel, also ist Seite c die Hypotenuse):
\( a^2 + b^2 = c^2 \\ c = \sqrt{a^2 + b^2} \\ c = \sqrt{(5,2915\;cm)^2 + (6\;cm)^2} \\ c = \sqrt{64\;cm^2} \\ c = 8\;cm \)
Winkel ∠ABC =
Winkel ∠CAB =
Skizze:
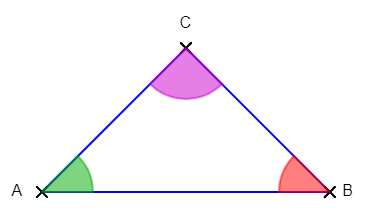
Seite AB =
5,657 cm
Winkel ∠ABC =
45°
Winkel ∠CAB =
45°
Bestimmen wir die beiden fehlenden Winkel:
Wir erkennen, dass Seiten BC und AC gleich lang sind, damit sind die beiden anliegenden Winkel ∠ABC und ∠CAB gleich groß.
∠ABC + ∠BCA + ∠CAB = 180°
∠ABC + ∠CAB = 180° - ∠BCA | ∠BCA = 90°
2·x = 180° - 90°
x = 45°
∠ABC = ∠CAB = 45°
Bestimmen wir die fehlende Seite (∠BCA ist rechter Winkel, also ist Seite ∠AB die Hypotenuse):
\( \overline{BC}^2 + \overline{AC}^2 = \overline{AB}^2 \\ \overline{AB} = \sqrt{\overline{BC}^2 + \overline{AC}^2} \\ \overline{AB} = \sqrt{(4\;cm)^2 + (4\;cm)^2} \\ \overline{AB} = \sqrt{32\;cm^2} \\ \overline{AB} ≈ 5,657\;cm \)
Winkel γ =
Seite a ≈ 6,245 cm
Winkel γ = 38,682°
Bestimmen wir den fehlenden Winkel:
γ = 180° - α - β = 180° - 51,318° - 90° = 38,682°
γ = 38,682°
Bestimmen wir die fehlende Seite (β ist rechter Winkel, also ist Seite b die Hypotenuse):
\( a^2 + c^2 = b^2 \\ a = \sqrt{b^2 - c^2} \\ a = \sqrt{(8\;cm)^2 - (5\;cm)^2} \\ a = \sqrt{39\;cm^2} \\ a ≈ 6,245\;cm \)
Winkel β =
Seite b ≈ 8,944 cm
Winkel β = 48,19°
Bestimmen wir den fehlenden Winkel:
β = 180° - α - γ = 180° - 90° - 41,81° = 48,19°
β = 48,19°
Bestimmen wir die fehlende Seite (α ist rechter Winkel, also ist Seite a die Hypotenuse):
\( b^2 + c^2 = a^2 \\ b = \sqrt{a^2 - c^2} \\ b = \sqrt{(12\;cm)^2 - (8\;cm)^2} \\ b = \sqrt{80\;cm^2} \\ b ≈ 8,944\;cm \)
Winkel β =
Seite c ≈ 86,023 cm
Winkel β = 54,462°
Bestimmen wir den fehlenden Winkel:
β = 180° - α - γ = 180° - 90° - 35,538° = 54,462°
β = 54,462°
Bestimmen wir die fehlende Seite (γ ist rechter Winkel, also ist Seite c die Hypotenuse):
\( a^2 + b^2 = c^2 \\ c = \sqrt{a^2 + b^2} \\ c = \sqrt{(50\;cm)^2 + (70\;cm)^2} \\ c = \sqrt{7400\;cm^2} \\ c ≈ 86,023\;cm \)
Winkel α =
Seite b = 1503,33 cm
Winkel α = 86,186°
Bestimmen wir den fehlenden Winkel:
α = 180° - β - γ = 180° - 90° - 3,814° = 86,186°
α = 86,186°
Bestimmen wir die fehlende Seite (β ist rechter Winkel, also ist Seite b die Hypotenuse):
\( a^2 + c^2 = b^2 \\ b = \sqrt{a^2 + c^2} \\ b = \sqrt{(1500\;cm)^2 + (100\;cm)^2} \\ b = \sqrt{2260000\;cm^2} \\ b ≈ 1503,33\;cm \)
