AB: Pythagoras im Alltag
Im Alltag trifft man auf viele Probleme, die sich mit Hilfe vom Satz des Pythagoras lösen lassen. Nachfolgend sind solche Situationen aufgezeigt, die es zu lösen gilt.
Benutze den Satz des Pythagoras, um die Aufgaben aus dem Alltag zu lösen.
Es sind zwei Punkte im Koordinatensystem gegeben. Punkt A(0|1) und Punkt B(2|3). Bestimme die Entfernung beider Punkte zueinander.
Wenn wir eine Strecke für die x-Werte der Punkte einzeichnen und eine Strecke für deren y-Werte, dann erhalten wir:
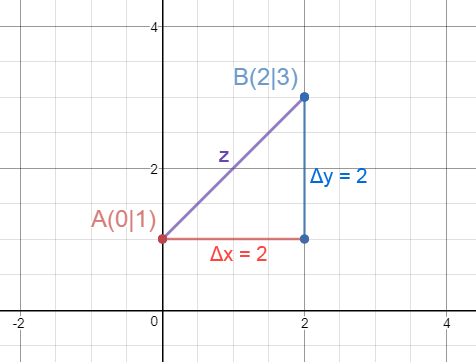
Das Zeichen Δ steht für den Abstand.
Wir können nun den Satz des Pythagoras anwenden, um die direkte Entfernung (z) zu berechnen:
Δx² + Δy² = z²
Setzen wir die Abstände ein und lösen auf:
2² + 2² = z²
4 + 4 = z²
z² = 8
z = √8 ≈ 2,83
Die Entfernung der beiden Punkte beträgt z = √8 bzw. gerundet z = 2,83 Längeneinheiten.
Wie lang muss eine Leiter sein, wenn sie bei einem Abstand von 1,20 m von einer Wand 4 m hoch sein soll?
Die Höhe beträgt 4 m, die Breite 1,20 m. Gesucht ist die Diagonale. Wir haben ein rechtwinkliges Dreieck und können direkt anwenden:
Diagonale d² = (4 m)² + (1,20 m)²
d² = 16 m² + 1,44 m²
d² = 17,44 m²
d = √17,44 m
d ≈ 4,18 m
Die Leiter muss mindestens 4,18 m lang sein, um bei einem Abstand von 1,20 m an die Höhe von 4 m zu reichen.
Eine Tür in einer Altbauwohnung ist 2,05 m hoch und 0,80 m breit. Passt ein 2,10 m breites und 3,40 m langes Brett hindurch?
Wir berechnen die Diagonale der Tür und wissen dann, wie lang das Brett maximal sein darf.
Diagonale d² = (2,05 m)² + (0,80 m)²
d² = 4,2025 m² + 0,64 m²
d² = 4,8425 m²
d = √4,8425 m
d ≈ 2,2 m
Das Brett passt durch die Tür, wenn man die Brettbreite (2,10 m) diagonal durch die Tür schiebt. Die Diagonale ist ca. 2,2 m.
Eine Seilbahn führt von einer 500 m hoch gelegenen Talstation auf das Skigebiet in 950 m Höhe. Die Luftlinie zwischen Tal- und Bergstation beträgt 2000 m. Wie lang ist die Seilbahn?
Die Höhendifferenz zwischen Talstation und Skigebiet ist: 950 m - 500 m = 450 m.
Die horizontale Differenz ist 2000 m.
Die Verbindung zwischen Talstation und Skigebiet ist die Diagonale (und wir haben ein rechtwinkliges Dreieck).
Diagonale d² = (450 m)² + (2000 m)²
d² = 202500 m² + 4000000 m²
d² = 4202500 m²
d = √4202500 m
d = 2050 m
Die Seilbahn ist 2050 m lang.
Bei einem 42-Zoll Bildschirm ist die Diagonale 107 cm lang. Wie hoch ist der Bildschirm, wenn dieser 93 cm breit ist?
Die Diagonale ist die Hypotenuse, die Breite und Höhe des Bildschirms sind die Katheten.
Wir kennen die Diagonale d = 107 cm und Breite b = 93 cm, und können nun die Höhe h berechnen:
\( d^2 = b^2 + h^2 \\ h^2 = d^2 - b^2 \\ h = \sqrt{d^2 - b^2} \\ h = \sqrt{(107 \;cm)^2 - (93 \;cm)^2} \\ h = \sqrt{11449 \;cm^2 - 8649 \;cm^2} \\ h = \sqrt{2800 \;cm^2} \\ h ≈ 52,9 \;cm \)
Die Höhe des Bildschirms beträgt ca. 52,9 cm.
In einem Glockenturm hängt das Seil zum Läuten der Glocke senkrecht herab. Wenn das Ende des Seils unten um 2 m nach rechts bewegt wird, hebt sich das Seilende um 10 cm. Wie lang ist das gespannte Seil?
Hier machen wir eine Skizze und nutzen die Variable s für die unbekannten Werte:
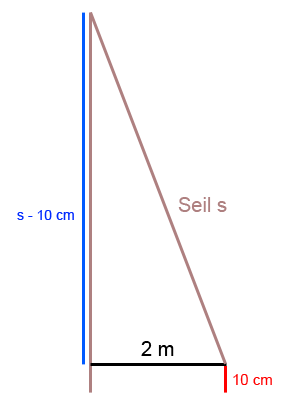
Wir erkennen, dass sich der Satz des Pythagoras wie folgt anwenden lässt:
Seillänge s² = (s - 10 cm)² + (2 m)²
s² = (s - 10)² + (200)²
s² = (s² - 2·s·10 + 100) + 40000
s² = s² - 20·s + 100 + 40000 | -s²
0 = -20·s + 40100 | +20·s
20·s = 40100 | :20
s = 2005 cm = 20,05 m
Das Seil hat eine Länge von 20,05 m.
