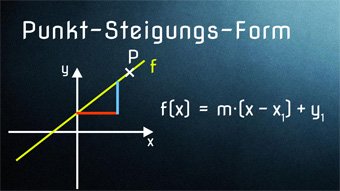
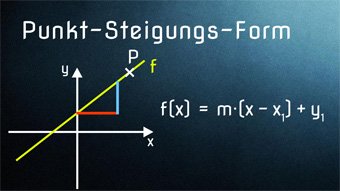
Lektion F05: Gleichung einer Linearen Funktion bestimmen
In diesen Mathevideos bestimmen wir die Gleichung einer linearen Funktion (die sogenannte Geradengleichung), indem wir die Steigung ermitteln und dann einen Punkt in die Normalform einsetzen. Voraussetzung zum Verstehen ist, dass ihr die Lektion Lineare Funktionen in Normalform gesehen habt. Denn dann wisst ihr, wie sich die Steigung eines linearen Graphen und der Schnittpunkt mit der y-Achse berechnet.
Gleichung einer linearen Funktion bestimmen
Wir zeigen, wie man mit Hilfe von 2 Punkten die Funktionsgleichung (Geradengleichung) eines linearen Graphen bestimmt. Anschließend Herleiten der Punkt-Steigungs-Form und Anwendung bei nur 1 Punkt und gegebener Steigung.
Zugriff auf Video nur als eingeloggter Benutzer.
Weitere Videos für Kunden:
-
F05-2 Gleichung bestimmen mit Punkt und ParallelenAufgabe zur Punkt-Steigungs-Form: Gleichung der Geraden bestimmen, die parallel zu einer anderen Geraden durch einen gegebenen Punkt verläuft. Erklärung der Bestandteile der Punkt-Steigungs-Form visuell im Koordinatensystem.
-
F05-3 Gleichung aus 2 Punkten bestimmen (LGS)Funktionsgleichung aus 2 Punkten ermitteln mit Hilfe vom Linearen Gleichungssystem und der Normalform. Anwendung von Gleichsetzungsverfahren und Subtraktionsverfahren.
-
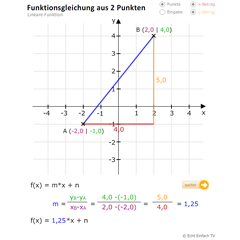Lineare Funktion aus 2 PunktenDieses Programm berechnet aus zwei Punkten die Funktionsgleichung einer linearen Funktion. Gebt auch eigene Punkte ein. Zusätzlich wird euch der Rechenweg angezeigt. -
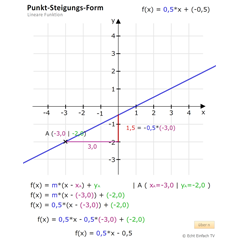Punkt-Steigungs-FormWählt einen beliebigen Punkt und eine beliebige Steigung für den linearen Graphen. Die Funktionsgleichung wird euch berechnet. -
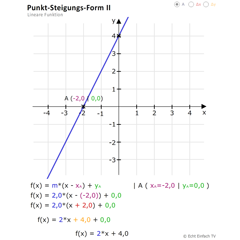Punkt-Steigungs-Form IILegt die Steigung der linearen Funktion fest und verschiebt dann den Punkt A. Die entstehende Geradengleichung wird angezeigt. -
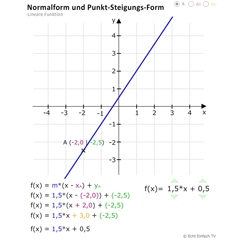Punkt-Steigungs-Form und NormalformGegenüberstellung von Normalform und Punkt-Steigungs-Form bei linearen Funktionen. Die Koeffizienten sind veränderbar, der Punkt verschiebbar.
Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.
Hier findest du 1 Lerncheck, mit dem du dein Wissen testen kannst.
Häufige Fragen:
- Wie funktioniert die Punktsteigungsform?
- Bestimme rechnerisch die Funktionsgleichung der linearen Funktion, deren Graph durch die Punkte P₁(2|0) und P₂(6|-6)
- Funktionsgleichung der Geraden durch P(1;-1) und Q(3;5) bestimmen
- Finde die Gleichung einer Geraden, die parallel zur Geraden g: y = 7x+1
- Habe ich diese Geradengleichung richtig gerechnet? m=-1 und P(3|4)
Finde weitere Fragen und Antworten in der Mathelounge.