AB: Lektion Gleichung einer Linearen Funktion bestimmen
Nachfolgend findet ihr Aufgaben zum Aufstellen von linearen Funktionsgleichungen, mit denen ihr euer neues Wissen testen könnt.
Bestimme die Funktionsgleichungen aus den gegebenen Informationen.
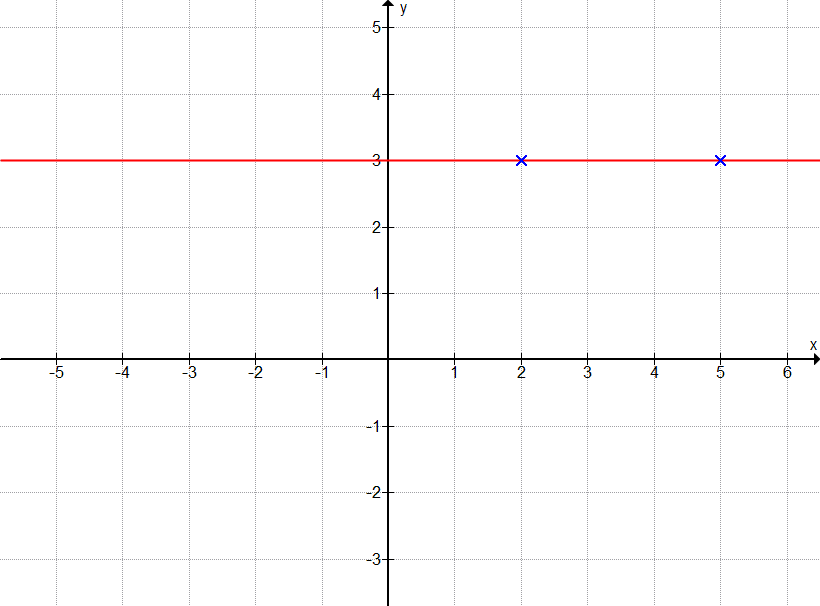
Punkte A(2|3), B(5|3)
Hier braucht man nur genau hinzuschauen. Man sieht, dass beide Punkte den y-Wert 3 haben. Das heißt, dass die entsprechende Gerade parallel zur x-Achse liegt. Sie wird durch f(x) = 3 beschrieben.
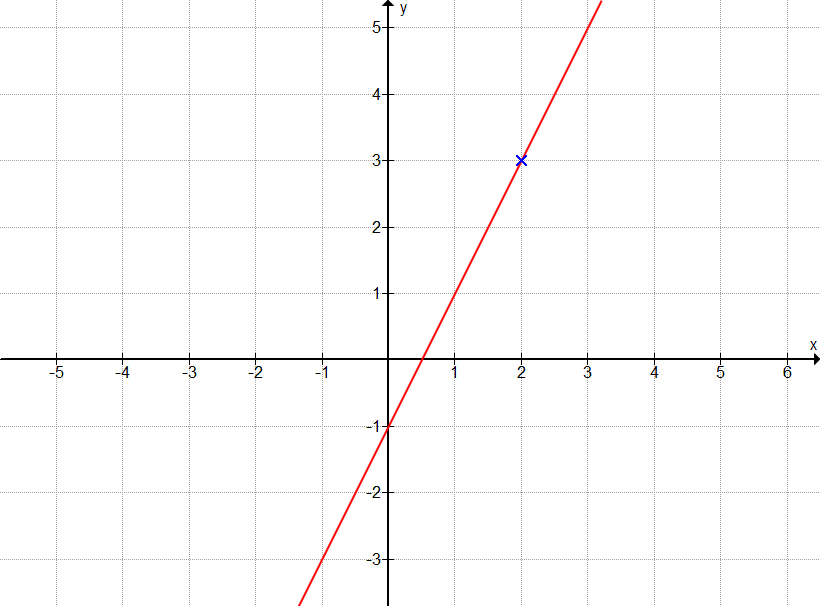
Punkte A(2|3), B(7|13)
Es gibt verschiedene Wege, die entsprechende Funktion aufzustellen. Entweder über ein Gleichungssystem, die Zweipunkteform oder zuerst die Steigung berechnen und dann mit der Punktsteigungsform fortfahren etc. Nutzen wir hier unser Wissen über das Gleichungssystem. Dazu setzen wir beide Punkte in die Allgemeinform der linearen Funktion (y = m·x + n) ein:
3 = 2·m + n
13 = 7·m + n
Beide Gleichungen seien hier nach n aufgelöst und gleichgesetzt. Es wird als das sogenannte Gleichsetzungsverfahren verwendet.
n = 3 - 2·m
n = 13 - 7·m
Jetzt gleichsetzen:
n = n
3 - 2·m = 13 - 7·m |+7·m -3
5·m = 10 |:5
m = 2
Diesen Wert nun in die erste Gleichung einsetzen:
3 = 2·m + n | m=2
3 = 2·2 + n
n = -1
Wir können die lineare Funktion also durch f(x) = 2·x - 1 beschreiben.
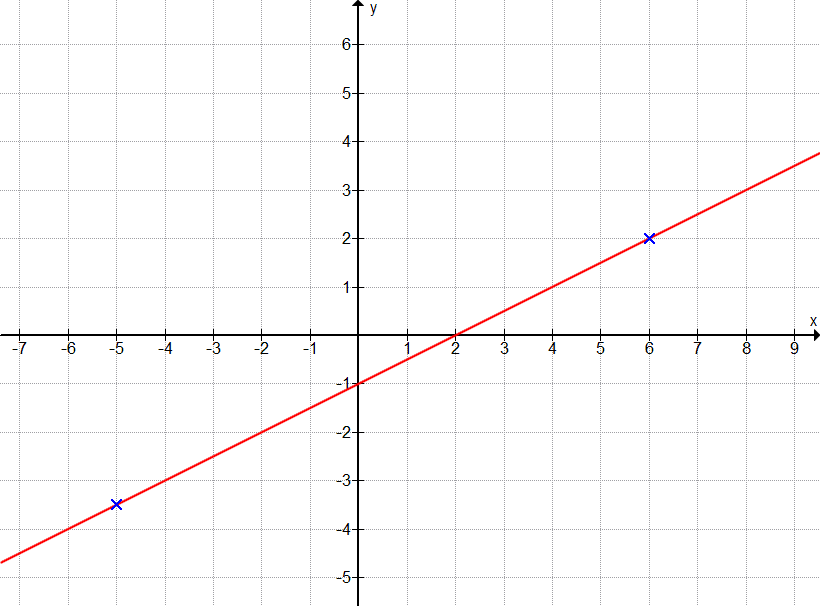
Punkte A(6|2), B(-5|-3,5)
Verwenden wir hier die Zweipunkteform, sie lautet:
\( f(x) = \frac{y_B - y_A}{x_B - x_A} · (x - x_A) + y_A \)
Setzen wir nun unsere Werte ein:
\( f(x) = \frac{-3,5 - 2}{-5 - 6} · (x - 6) + 2 \\ f(x) = \frac{-5,5}{-11} · (x - 6) + 2 \\ f(x) = 0,5 · (x - 6) + 2 \\ f(x) = 0,5·x - 3 + 2 \\ f(x) = 0,5·x - 1 \)
Die Funktionsgleichung bzw. Geradengleichung wird also beschrieben durch f(x) = 0,5·x - 1.
m = 3 und Punkt A(7|2)
Verwenden wir direkt die Punktsteigungsform, die da lautet: f(x) = m·(x - xA) + yA. Es ergibt sich:
f(x) = m·(x - xA) + yA
f(x) = 3·(x - 7) + 2
f(x) = 3·x - 21 + 2
f(x) = 3·x - 19
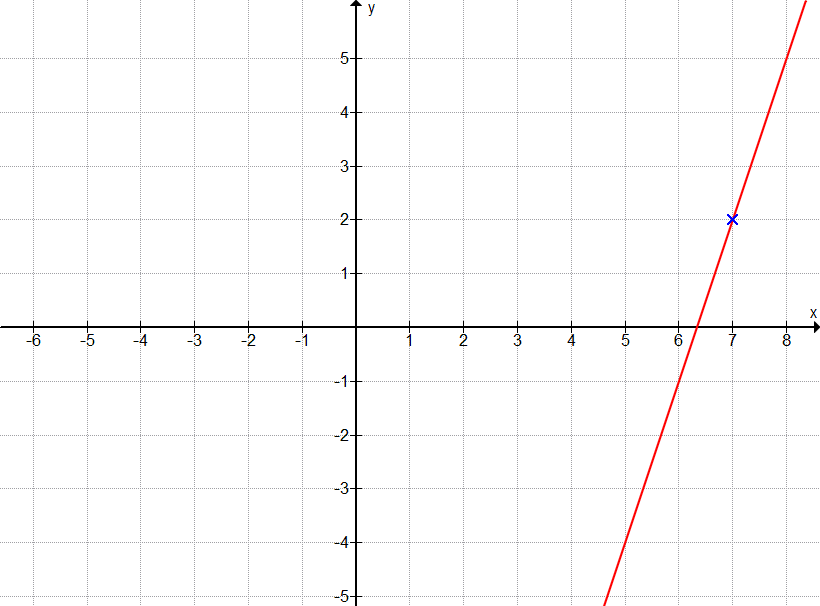
m = -0,5 und Punkt A(2|2)
Hier können wir alternativ die bekannten Werte (xA = 2, yA = 2, m=2) in die Allgemeinform der linearen Funktion einsetzen, also in f(x) = m·x + n.
f(x) = m·x + n = y
-0,5·2 + n = 2
-1 + n = 2 |+1
n = 3
Folglich: f(x) = -0,5·x + 3
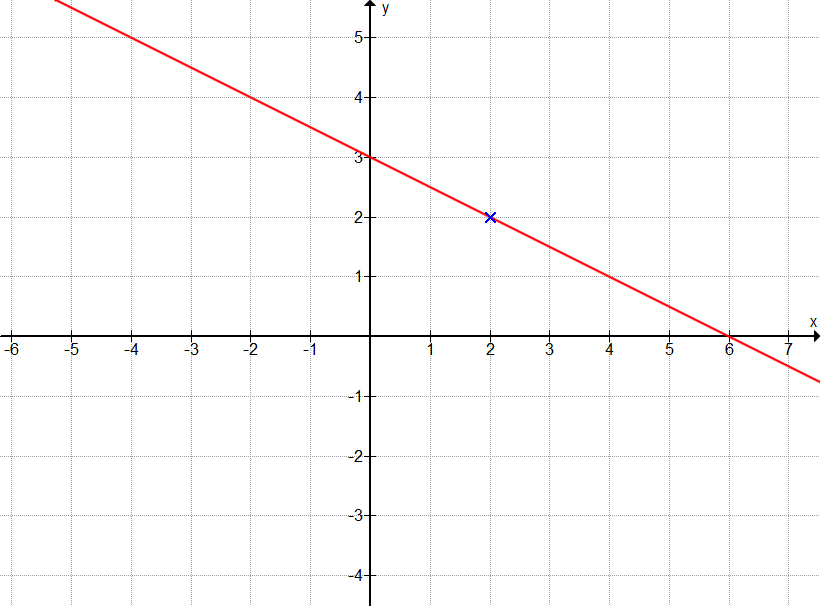
Der Graph verläuft durch den Ursprung und hat die Steigung m = 2.
Hier ist es zuerst Aufgabe zu verstehen, was „durch den Ursprung“ bedeutet. Das bedeutet nichts anderes, als dass die Gerade durch den Punkt O(0|0) geht. Da kann man sich nun die Punktsteigungsform zu Hilfe nehmen und die Geradengleichung bestimmen. Alternativ kann man sich erinnern, dass der y-Wert bei x = 0 dem y-Achsenabschnitt n entspricht. Hier ist also n = 0. Zudem ist m = 2 bekannt. Wir haben also f(x) = 2·x.
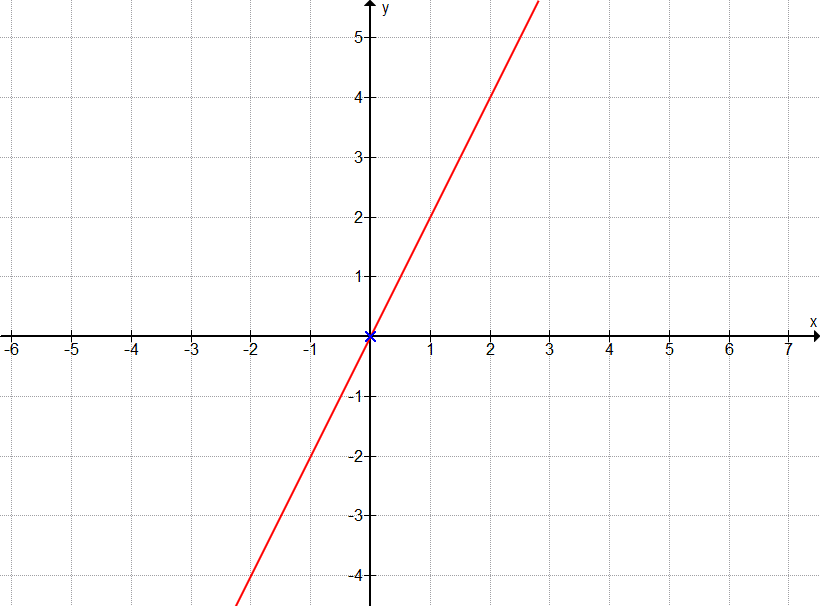
Parallel zur Geraden g(x), welche sich bildet durch m = 2 und A(2|3). Die gesuchte Gerade f(x) geht durch B(2|5).
Auch hier ist es erst einmal die Aufgabe, die Beschreibung zu verstehen. Parallel indiziert sofort, dass beide Geraden die gleiche Steigung haben. Das heißt, kennt man die Steigung der einen Geraden, dann kennt man auch die der anderen. Es ist hier also unnötig g(x) genauer zu bestimmen, da die wichtige Information (die Steigung) bereits bekannt ist. Gehen wir also direkt zur Bestimmung der Gleichung von f. Die Punktsteigungsform ergibt:
f(x) = m·(x - xB) + yB
f(x) = 2·(x - 2) + 5
f(x) = 2·x - 4 + 5
f(x) = 2·x + 1
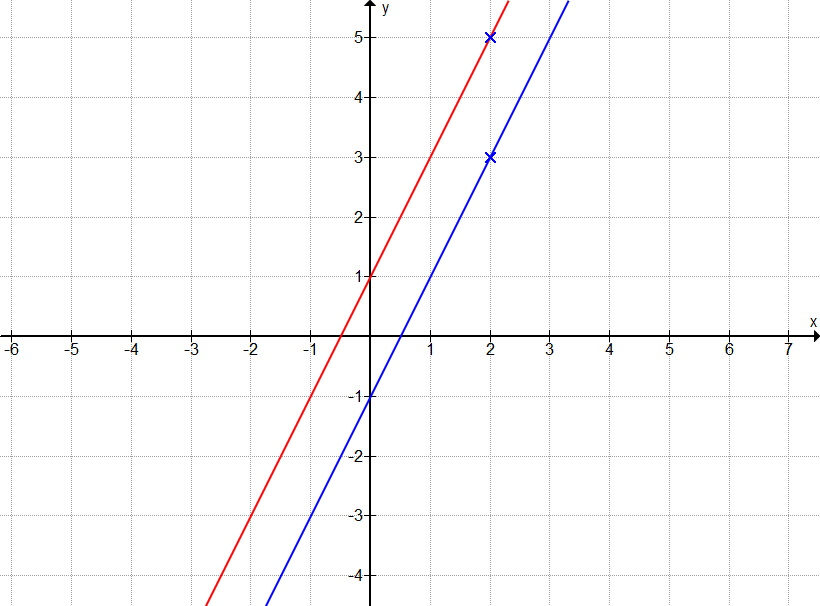
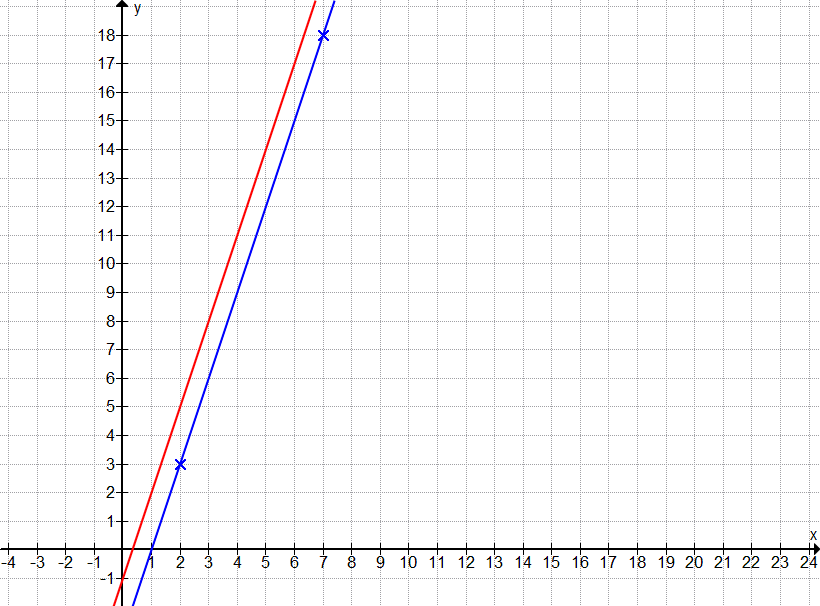
Parallel zur Geraden g(x), welche sich bildet durch A(2|3) und B(7|18). Sie ist um 2 nach oben verschoben.
Hier ist es nicht ganz so einfach. Die Steigung kann zuerst bestimm werden, dafür kann man direkt die Steigung aus A und B berechnen.
\( m = \frac{y_B - y_A}{x_B - x_A} \)
\( m = \frac{18 - 3}{7 - 2} = \frac{15}{5} = 3 \)
m = 3
Die gesuchte Steigung ist m = 3, das ist hier aber zur Lösung nicht ausreichend. Wir müssen diesmal mehr von g(x) wissen, denn die gesuchte Gerade ist um 2 nach oben verschoben. Errechnen wir g(x), indem wir n bestimmen. Einsetzen von m und A(2|3):
f(x) = m·x + n = y
3·2 + n = 3
6 + n = 3 |-6
n = -3
Die Gerade g hat die Funktionsgleichung g(x) = 3·x - 3. Die Gerade f ist nun um 2 nach oben verschoben. Das erreichen wir mittels Addition von 2.
f(x) = g(x) + 2
f(x) = (3·x - 3) + 2
f(x) = 3·x - 1