AB: Flächengleichheit/Puzzles (7)
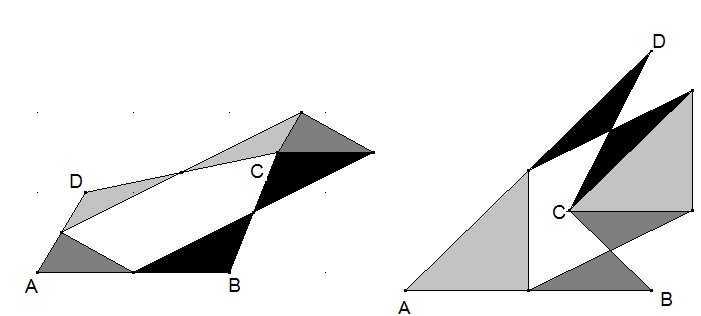
Beliebiges Viereck wird Parallelogramm: Scheiden Sie drei Ecken eines beliebigen Vierecks ABCD so ab, dass die vier Stücke zu einem Parallelogramm zusammengelegt werden können.
Legen Sie jeden Schnitt durch zwei Seitenmitten. In den Abbildungen (links: konvexes Viereck, rechts: konkaves Viereck) haben abgeschnittene Ecken die gleiche Tönung, wie wieder angelegte Stücke.
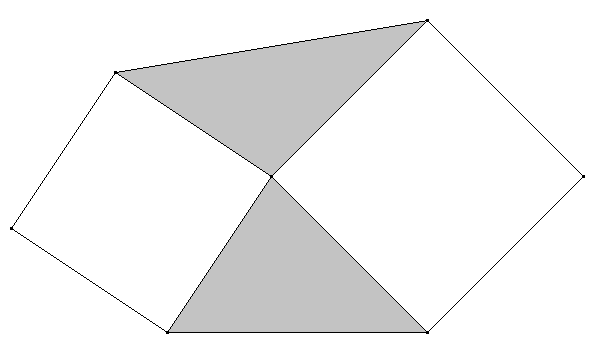
Dreiecke zwischen Quadraten:
Zwei Quadrate unterschiedlicher Größe haben eine Ecke gemeinsam. Sonst ist die Lage zueinander beliebig. Die gemeinsame Ecke ist gleichzeitig Eckpunkt zweier Dreiecke, welche die Zwischenräume zwischen den Quadraten ausfüllen (in der Abbildung grau unterlegt). Zeigen Sie: Die grauen Dreiecke sind flächengleich.
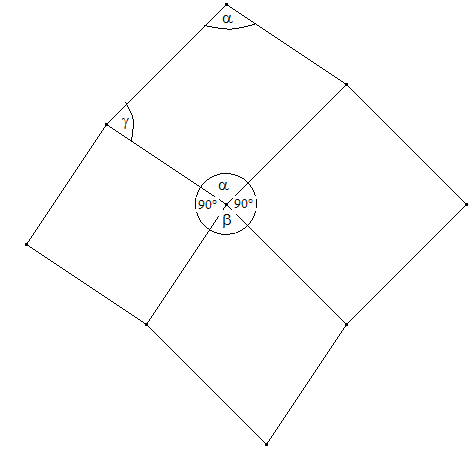
Ergänze die Dreiecke zu Parallelogrammen. Dann ist (1) γ+α=180° und α+90°+β+90°=360°also (2) α+β=180°. Wegen (1) und (2) ist β=γ. Parallelogramme sind kongruent, wenn die in zwei unterschiedlichen Seitenlängen und der Größe eines Winkels übereinstimmen. Die grauen Dreiecke der Aufgabe sind Hälften von kongruenten Parallelogrammen und daher flächengleich.
Die Quadrate über den Seiten eines beliebigen Dreiecks werden so ergänzt, dass ihre Zwischenräume von Dreiecken aufgefüllt werden (in der Abbildung grau unterlegt). Zeigen Sie, dass alle grauen Dreiecke flächengleich sind.
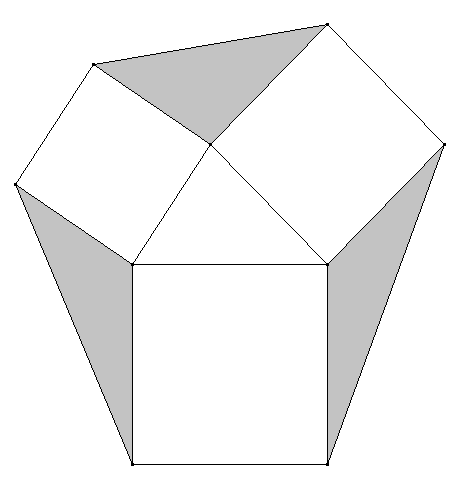
Jedes der grauen Dreiecke ist (nach Aufgabe a) flächengleich zum gleichen Dreieck (in der Mitte). Daher sind alle grauen Dreiecke flächengleich.
Über den Seiten von zwei grauen Dreiecken werden Quadrate errichtet (Abbildung nächste Seite). Wie groß ist die dunkelgraue Fläche dazwischen im Vergleich zu einem hellgrauen Dreieck?
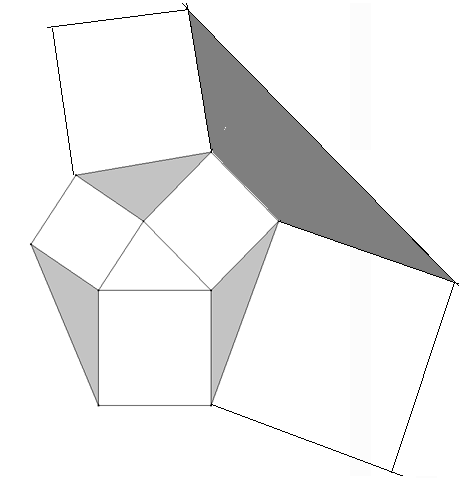
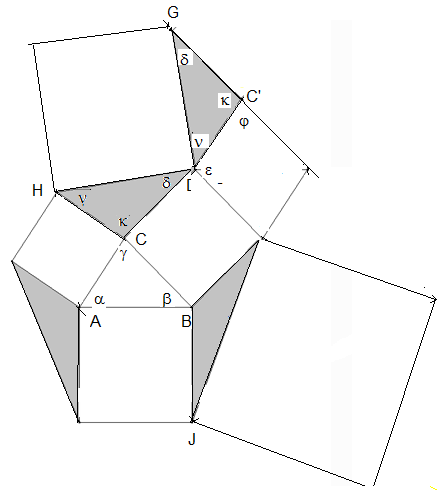
In der linken Abbildung unten ist δ=μ, denn beide werden von λ zu 180° ergänzt. Dann lässt sich das Dreieck CDH in den Winkel FGD einpassen, sodass C auf C‘ fällt (rechte Abbildung).
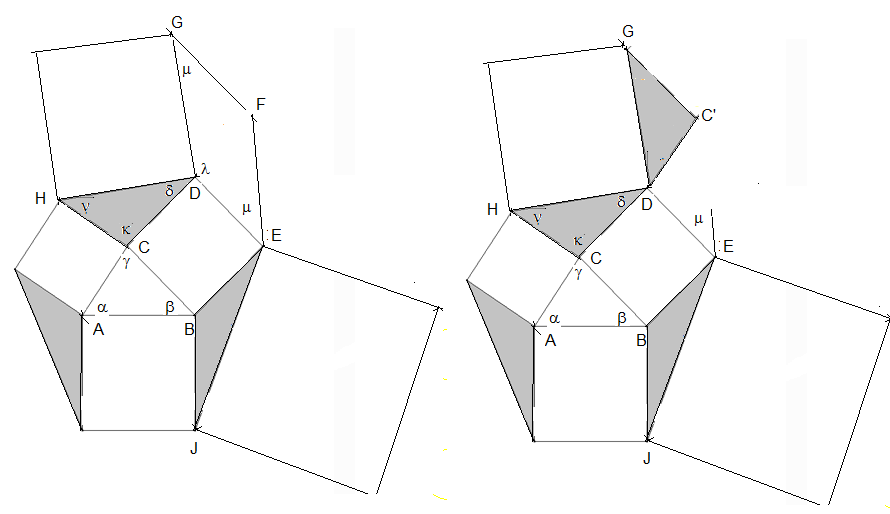
In die rechte Abbildung fügen wir Winkelbezeichnungen ein (siehe links). Jetzt gilt δ+ν+ε=180° und δ+ν+κ=180°. Daher ist ε=κ und κ=α+β (sowohl κ als auch α+β ergänzen sich mit γ zu 180°).
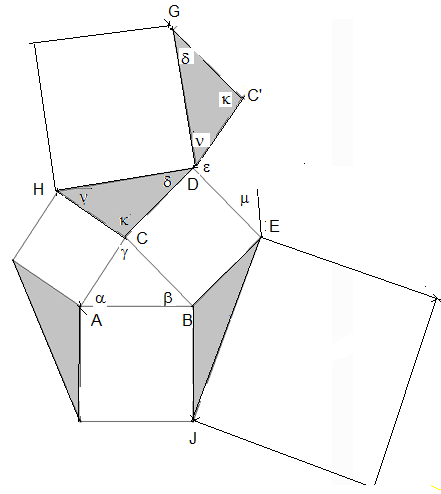
Die Strecke C‘G wird über C‘ hinaus verlängert (siehe links). Jetzt ist κ+θ=180°, also α+β+θ=180° und ebenfalls α+β+γ=180°, Daher ist θ=γ und das Dreieck ABC lässt sich in den Winkel θ einfügen (siehe unten).
In der gleichen Weise, wie das Dreieck CDH lässt sich das Dreieck JEB in die bei F liegende Ecke des Dreiecks EFB‘ einpassen. Damit liegen vier Dreiecke im Viereck DEFG, die nach Aufgabenteil b) alle flächengleich zu ABC sind.
Die dunkelgraue Fläche ist so groß, wie fünf hellgraue Flächen.
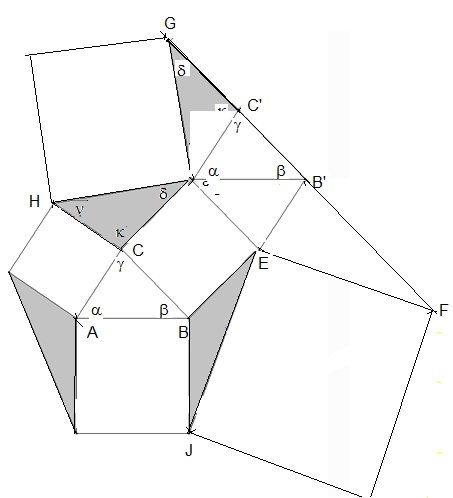
Zusammensetzung der Flächen.

Halbe Dreiecksfläche:
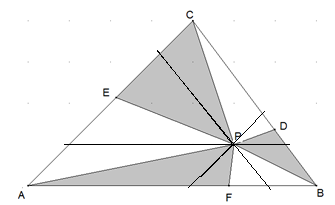
P sei ein beliebiger Punkt im Inneren des Dreiecks ABC und PH sowie PG Parallelen zu den Dreiecksseiten. PE sei Parallele zu einer Seitenhalbierenden durch B im Dreieck ABC. Warum halbiert PE die Fläche des Dreiecks GPH?
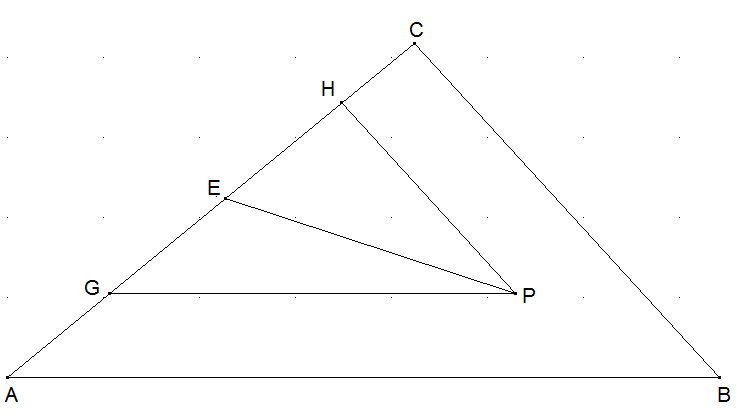
Die Dreiecke ABC und GPH stimmen in den Größen der Innenwinkel überein und sind daher ähnlich. Sind entsprechende Seiten ähnlicher Dreiecke parallel, so sind auch entsprechende Seitenhalbierende parallel. Die Seitenhalbierende eines Dreiecks halbiert die Fläche des Dreiecks. FGPE=FEPH.
P sei ein beliebiger Punkt im Inneren des Dreiecks ABC. PD, PE und PF seien Parallelen zu den Seitenhalbierenden. Zeigen Sie: Die graue Fläche ist ebenso groß, wie die weiße Fläche.
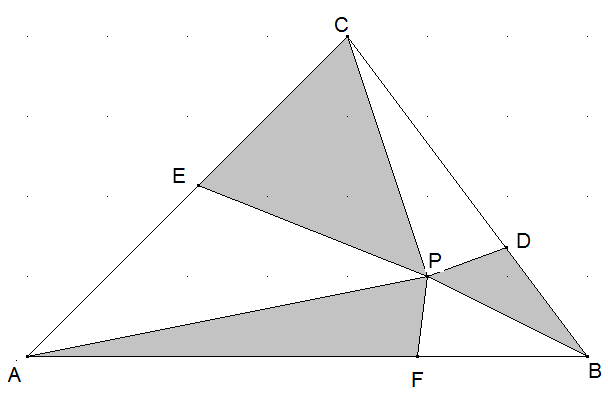
Die Parallelen zu den Dreiecksseiten zerlegen jede graue Fläche und jede weiße Fläche in je zwei Teilflächen, von denen zu jeder grauen Teilfläche eine gleichgroße weiße Teilfläche existiert.