AB: Beweisen und Rechnen mit Kreisen (2)
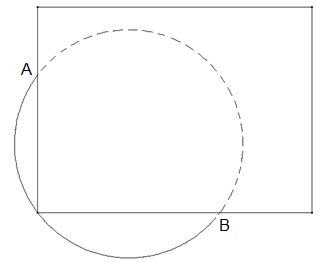
Verlorener Mittelpunkt eines Kreises: Wie kann man nur mit Hilfe einer Postkarte und einem Stift den Mittelpunkt eines Bierdeckels finden?
Legen Sie die Postkarte mit einer Ecke auf den Rand des Bierdeckels. Markieren Sie auf dem Bierdeckel die Punkte A und B, an denen der Rand des Bierdeckels auf den Rand der Postkarte trifft. Dann ist AB der Durchmesser des Bierdeckels (Thaleskreis). Konstruieren Sie auf die gleiche Weise einen zweiten Durchmesser. Die Durchmesser schneiden sich im Mittelpunkt des Bierdeckels.
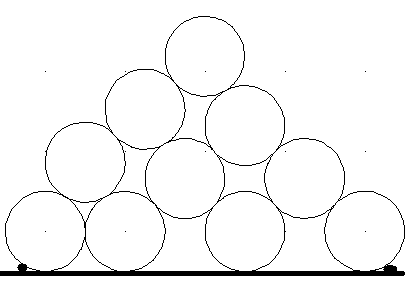
Gestapelte Rohre: Ein Stapel von Rohren wurde schon in der untersten ebenen Lage nicht ordentlich begonnen. Begründen Sie, dass das oberste Rohr genau mittig zwischen dem rechten und dem linken untersten Rohr liegt.
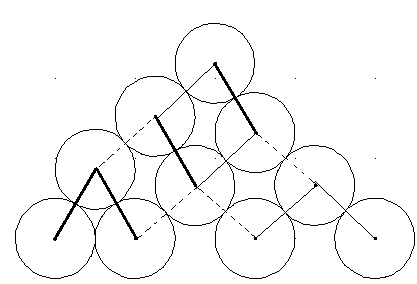
Strecken gleicher Strichstärke haben gleichlange Projektionen auf eine gemeinsame Waagerechte. Die Summe der Projektionen der drei verschieden dargestellten Strecken auf eine Waagerechte ist rechts und links gleich.
Kreisteilung: A7, A8, A3 und A4 sind Achtel-kreise zum Radius r1. A2 und A6 sind Halbkreise zum Radius \({r_2} = \frac{1}{2}{r_1}\). Zeigen Sie A1 = A2 = … = A7 = A8.
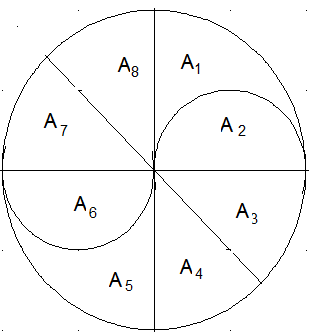
Sei r der Radius des großen Kreises, dann ist A1=, A2=, A3=\(\frac{\pi {r^2}}{8}\). Demnach ist A1=A2=A3. Für den Vergleich anderer Flächenstücke folgt Entsprechendes.
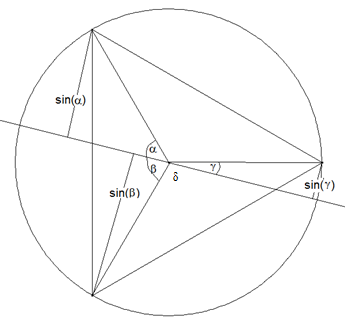
Lote auf einen Durchmesser des Umkreises: Auf einen beliebigen Durchmesser des Umkreises eines gleichseitigen Dreiecks werden die Lote von den Eckpunkten des gleichseitigen Dreiecks gefällt. Zeigen Sie: Die beiden kürzeren Lote sind zusammen so lang, wie das längere Lot.
Der Umkreis habe den Radius 1. Die Radien zu den Eckpunkten des gleichseitigen Dreiecks bilden mit einem beliebigen Durchmesser die Winkel α, β und γ. Die Lote von den Eckpunkten des gleichseitigen Dreiecks auf den Durchmesser haben dann die Längen sin(α), sin(β) und sin(γ). Nun gilt: α+β=120° oder β=120°–α. Außerdem gilt β+δ=180° und γ+δ=120°. Dann ist γ=ß–60°. Hier β eingesetzt ergibt: γ= 60°–α. Dann ist sin(α) + sin(γ) = sin(β). Um dies zu zeigen benötigt man das Additionstheorem für sin(x–y) und die Gleichungen sin(120°) = sin(60°) = \(\frac{\sqrt{3} }{2}\) sowie cos(120°) = –\(\frac{1}{2}\) und cos(60°) = \(\frac{1}{2}\).