AB: Satz des Pythagoras und verwandte Sätze (4)
Pythagoras visualisiert: In einem Quadrat mit der Seitenlänge c werden die Quadrate mit den Flächen a² und b² so untergebracht, dass zunächst einige Flächenteile überstehen (siehe Abbildung). Zeigen Sie, dass sich die Überstände ebenfalls im Quadrat mit der Seitenlänge c unterbringen lassen.
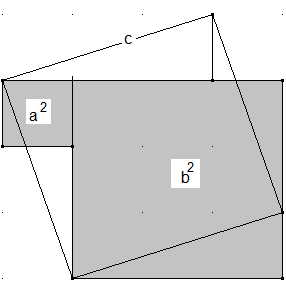
Verschieben Sie die Überhänge außerhalb des großen Quadrats in die Flächen gleicher Färbung innerhalb des großen Quadrats.
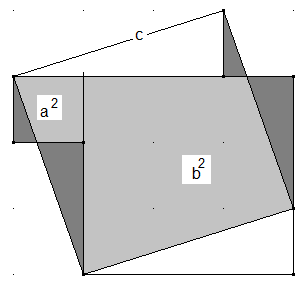
Kreisring: Zwei Kreise mit gleichem Mittelpunkt schließen einen sogenannten Kreisring ein. Wie groß ist der Flächeninhalt des Kreisringes (grau unterlegt), wenn der große Kreis aus der Tangente an den kleinen Kreis in einem Punkt B eine Strecke \( \overline {AC} \) mit der Länge 8 cm herausschneidet?
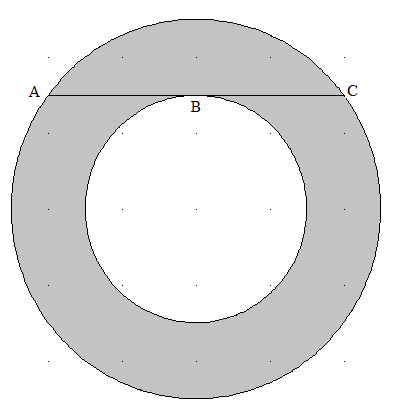
R sei der Radius des äußeren Kreises und r der Radius des inneren Kreises. Dann ist π·R²-π·r²=π·(R²-r²) der Flächeninhalt des Kreisringes. Außerdem gilt nach Pythagoras R²-r²=16. Die Fläche des Kreisringes ist also 16π.
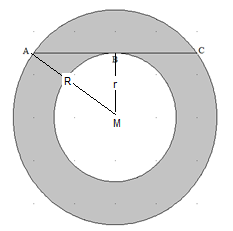
Sehnenvierecke mit besonderen Eigenschaften: Gesucht sind die Umkreise von Sehnenvierecken mit zwei gegenüberliegenden Winkeln von je 90° und vier verschiedenen Seitenlängen sowie deren Konstruktionsprinzipien. Erklären Sie, wie Ihnen (w²+x²)·(y²+z²) = (wy+xz)²+(wz-xy)²=(wz+xy)²+(wy-xz)² bei der Lösung dieser Aufgaben helfen kann.
Für Sehnenvierecke mit den Seitenlängen a, b, c und d sowie zwei gegenüberliegenden rechten Winkeln muss gelten a² + b² = c² + d². Für a=wy+xz, b=wz-xy, c=wz+xy und d=wy-xz hilft die gegebene Gleichung, diese Bedingung zu erfüllen. Der Durchmesser des Umkreises ist dann \( \sqrt{(w^2+x^2)·(y^2+z^2)} \).
Trapez und Pythagoras: Gegeben ist ein Trapez mit den Längen a und b der parallelen Seiten. Eine weitere Seite ist gleichzeitig Höhe des Trapezes und hat die Länge a+b (siehe Skizze). Beweisen Sie mit dieser Figur den Satz von Pythagoras.
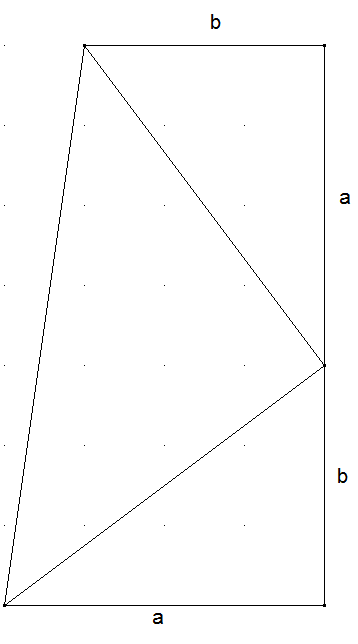
Die Trapezfläche berechnet sich einerseits als ½·(a+b)·(a+b) und andererseits als ½·ab + ½·ab + ½·c². Dann ist (a+b)² = 2ab + c² oder a² + 2ab + b² = 2ab + c² und dann a² + b² = c².
