CHECK: Knobelaufgaben I
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Löse das Zahlenmuster von Fabian
Fabian hat sich ein Zahlenmuster ausgedacht:
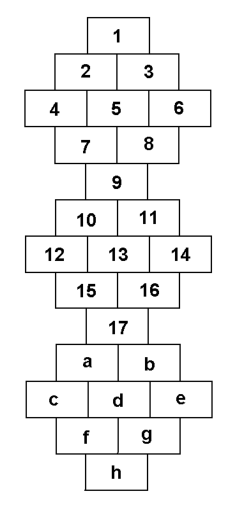
Wie geht das Muster weiter?
Schreibe die Zahlen auf, die anstelle der Kleinbuchstaben stehen müssen.
Bestimme die zweistellige natürliche Zahl.
Bestimme diejenige zweistellige natürliche Zahl, deren Quersumme 13 ist und bei der die Differenz aus der ursprünglichen Zahl und der Zahl, die man durch Vertauschen der beiden Ziffern erhält, auf 7 endet.
Wieviel Äpfel sind im Korb?
Alex, Bernd, Erik und Felix haben einen Korb Äpfel gepflückt und teilen alle Äpfel vollständig auf. Axel nimmt sich den vierten Teil der der Äpfel im Korb, Bernd nimmt zwei weniger als ein Drittel der Äpfel im Korb, Erik nimmt sechs weniger als die Hälfte der Äpfel im Korb. Felix nimmt drei Äpfel mehr als die Hälfte der Äpfel, die Axel genommen hat.
Wieviel Äpfel sind im Korb?
Eine Frage des Alters
Die Ziffern eines Menschenalters seien Elemente der Menge aller Primzahlen. Die Quersumme der Quersumme des Alters ist kleiner als die kleinste Primzahl. Diese Beschreibung gilt sowohl für eine Mutter als auch für ihr Kind. Wie alt war die Mutter, als sie das Kind gebar?
Die Ziffern eines Menschenalters seien Elemente der Menge aller Primzahlen.
{2,3,5,7}
Die Quersumme der Quersumme des Alters ist kleiner als die kleinste Primzahl.
Die kleinste Primzahl ist 2 - kleiner kann da nur 0 oder 1 sein.
Null scheidet aus, da dies nur für das Säuglingsalter möglich ist - später jedoch eine Mutter gefordert ist.
Die Quersumme einer Quersumme, welche 1 beträgt, kann nur aus 1 und Nullen erzeugt sein. Da es um Menschenalter geht kämen in Frage: 001;010;100
001 scheidet wegen der Kleinkind-Mutter-Diskrepanz und der Nichtprimeigenschaft von 1 aus. 100 erfordert mehr Stellen als ein Menschenalter haben kann. 010 kann aus zwei oder auch 3 Ziffern zusammengesetzt sein. Bei 3 Ziffern, müsste die kleinstmögliche Hunderterstelle den Wert 2 haben (Primzahl gefordert) - daher ist weitere Überlegungen unter Berücksichtigung der „Definitionsmenge Menschenalter“ hinfällig. Also muss die 10 aus 2 Ziffern kombiniert werden:
1+0=10 weder 1 noch Null ist prim
2+8 =10 hier ist 8 leider keine Primzahl
3+7=10 möglich
4+6=10 weder 4 noch 6 ist prim
5+5=10 möglich
…
Es bleiben also drei Varianten: 37, 55, 73
Diese Beschreibung gilt sowohl für eine Mutter als auch für ihr Kind.
Da Mutter und Kind nicht gleich alt sein können, bleiben 37 fürs Kind und 73 für die Mutter
Wie alt war die Mutter, als sie das Kind gebar?
73 - 37 = 36 Jahre
Sessellift: Während der Bergfahrt kommen dir 57 Sessel entgegen. Wie viele Sessel sind gerade im Umlauf?
Wir zählen alle Sessel zusammen: 57 (gezählt) + 1 (auf dem man sitzt) und dann noch je 1 oben und unten, die gerade im Rondell sind und daher nicht gekreuzt werden. Also ca. 60.
Da moderne Bügellifte unterschiedliche Techniken haben, sind es ca. 60. Es ist oft so, dass die Sessel direkt hinter den Passagieren drehen.
Ersetze die Buchstaben so durch Ziffern, dass die Rechnung stimmt.
In dem Schema
V I E R
+ V I E R
= A C H T
sind die Buchstaben so durch Grundziffern zu ersetzen, dass man eine richtige gelöste Additionsaufgabe erhält, deren Summe möglichst groß ist. Gleiche Buchstaben bedeuten dabei gleiche Grundziffern, verschiedene Buchstaben bedeuten verschiedene Grundziffern.
Welche Zahl steht für ACHT?
Um eine möglichst große Summe zu bekommen, wählt man die Zahlen so, dass bei so vielen wie möglich ein Übertrag entsteht. Also V+V+1 = A. Dann kann A = 9 und V = 4 gelten. Wegen A ≠ I kann I nicht 9 sein. Also setzen wir I = 8, damit der Hunderter der Sumem möglichst groß wird, und C = 7 (Ergebnis bei Übertrag 1 von der Summe E+E). Für E = 6 erhalten wir H = 3, wenn wir R so wählen, dass R+R > 9 gilt. Die größte noch nicht vergebene Zahl < 10, für die das gilt, ist R = 5, womit T = 0 sein muss.
Zerlege 200 in zwei ganzzahlige Summanden, so dass der eine durch 13, der andere durch 19 teilbar ist.
57 ist durch 19 teilbar: 57/19 = 3
143 ist durch 13 teilbar: 143/13 = 11
Zerlege die Zahl 45 in 4 Summanden.
Die Zahl 45 ist in 4 Summanden zu zerlegen, sodass man stets dieselbe Zahl erhält, wenn man zum ersten Summanden 2 addiert, vom zweiten Summanden 2 subtrahiert, den dritten Summanden mit 2 multipliziert und den vierten Summanden durch 2 dividiert.
8 + 2 = 10
12 - 2 = 10
5 · 2 = 10
20 : 2 = 10
Krähen auf dem Dach
Auf einem Hausdach sitzen Krähen links und rechts vom Schornstein. Wenn eine Krähe von rechts nach links fliegt, sitzen links doppelt so viele Krähen wie rechts. Fliegt hingegen eine Krähe von links nach rechts, sitzen auf beiden Seiten gleich viele Krähen. Wie viele Krähen sitzen auf dem Dach?
Tipp: Löse mittels Gleichungssystem.
Ist L die Anzahl der Krähen links, R die Anzahl der Krähen rechts, dann gilt
L+1 = 2·(R-1)
L-1 = R+1
Aus der zweiten Gleichung folgt:
L = R+2
Einsetzen in Gleichung 1 und auflösen nach R:
R+3 = 2·R-2, also R = 5 und L = 7
Lösung: 5+7=12
Lauter Quadratzahlen: Wie alt ist Alex?
Alex, sein Vater und sein Großvater sind zusammen genau 139 Jahre alt. Das Alter eines jeden ist eine Quadratzahl. Wie alt ist Alex?
Wäre Alex 1 Jahr, müssten sein Vater und sein Großvater gleich alt sein, nämlich 64 Jahre. Das geht offensichtlich nicht.
Wäre Alex 4 Jahre alt, so müssten sein Vater und sein Großvater zusammen 135 Jahre alt sein. Das Alter des Vaters und des Großvaters müssten auf 6 und 9 (oder umgekehrt) enden, damit die Summe auf 5 endet.
Mögliche Zahlen wären 36 und 49, aber die sind zusammen deutlich kleiner als 135. Für das Alter 4 gibt es also keine Lösung.
Wäre Alex 16 Jahre alt, so müssten sein Vater und sein Großvater zusammen 123 Jahre alt sein. Es gibt keine zwei Quadratzahlen, deren Summe auf 3 endet. 16 Jahre ist also nicht möglich.
Angenommen, Alex ist 9 Jahre alt. Dann sind sein Vater und sein Großvater zusammen 130 Jahre alt. Das Alter des Vaters und des Großvaters sollten dann auf 1 und 9 enden, damit die Summe auf 0 endet.
Dies gilt für 49 und 81. Tatsächlich ist 49 + 81 = 130. Alex kann 9, sein Vater 49 und sein Großvater 81 Jahre alt sein.
Fortschritt:
