CHECK: Pythagoras Gemischtes II
Um diese Seite nutzen zu können, musst du eingeloggt sein. – Neu hier? Dann registriere dich.
Berechne den Flächeinhalt eines Rechtecks, dessen Länge a = 175 cm beträgt und seine Diagonale e = 204 cm.
Die Flächenformel für Rechtecke lautet: A = a · b. Wir sehen, wir benötigen die noch unbekannte Seite b. Bestimmen wir b mit Hilfe vom Satz des Pythagoras:
a² + b² = e²
b² = e² - a²
b² = (204 cm)² - (175 cm)²
b² = 10991 cm²
b = √10991 cm
Folglich ist:
A = a · b
A = 175 cm · √10991 cm
A ≈ 18346,64 cm²
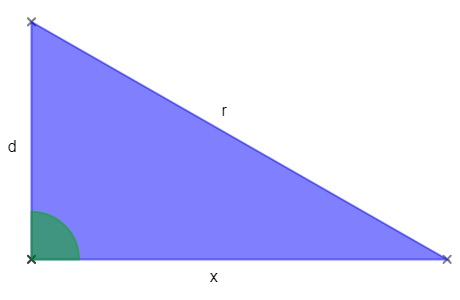
Gib den Satz des Pythagoras für das Dreieck d, x, r an.
Die Katheten sind d und x. Die Hypotenuse ist r.
Demnach gilt: r² = d² + x² bzw. d² + x² = r².
Berechne die Länge der Hypotenuse c für das rechtwinklige Dreieck mit den Seiten a = 3 m und b = 5 m.
a² + b² = c²
c² = a² + b²
c² = (3 m)² + (5 m)²
c² = 9 m² + 25 m²
c² = 34 m²
c = √34 m
c ≈ 5,83 m
Berechne die Länge der fehlenden Kathete im rechtwinkligen Dreieck mit den Seiten a = 5 m und c = 13 m.
a² + b² = c²
b² = c² - a²
b² = (13 m)² - (5 m)²
b² = 169 m² - 25 m²
b² = 144 m²
b = √144 m
b = 12 m
Es sei das rechtwinklige Dreieck gegeben mit a = 8 mm und b = 15 mm. Entspricht die Länge der Hypotenuse c einer Zahl aus den natürlichen Zahlen?
Errechnen wir die Hypotenuse c mit dem Satz des Pythagoras:
c² = a² + b²
c² = (8 mm)² + (15 mm)²
c² = 289 mm²
c = √289 mm
c = 17
Die Hypotenuse ist 17 mm lang. 17 ist eine natürliche Zahl, also: 17 ∈ ℕ.
Bei den Zahlen {8, 15, 17} handelt es sich um ein sogenanntes „Pythagoreisches Tripel“.
Fortschritt: