AB: Regelmäßige n-Ecke und n,k-Sterne (5)
Die 6,2-Sterne: Sowohl in das gleich-seitige Dreieck (2) als auch in drei Sterne (3) passen 36 gleich-seitige Dreiecke (1):
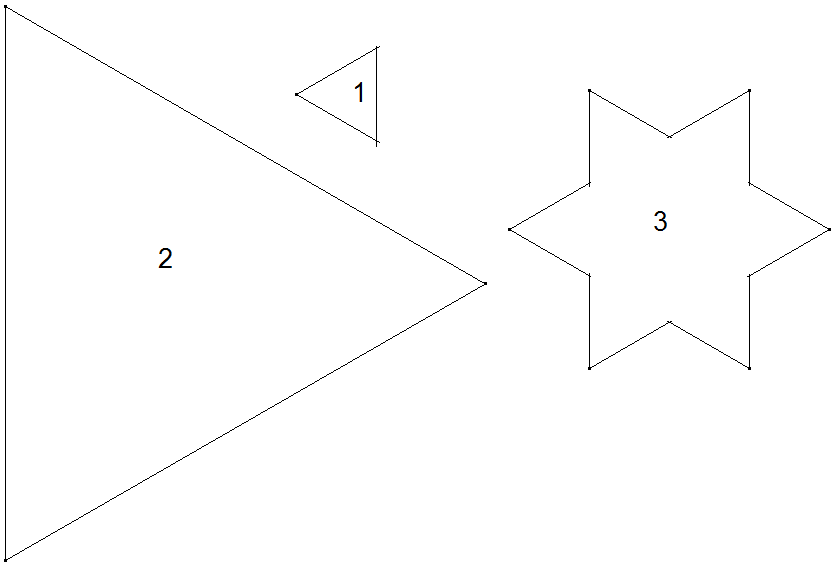
In welche minimale Anzahl von Teilen muss man drei Sterne (3) zerlegen, um damit das gleichseitige Dreieck (1) auslegen zu können.
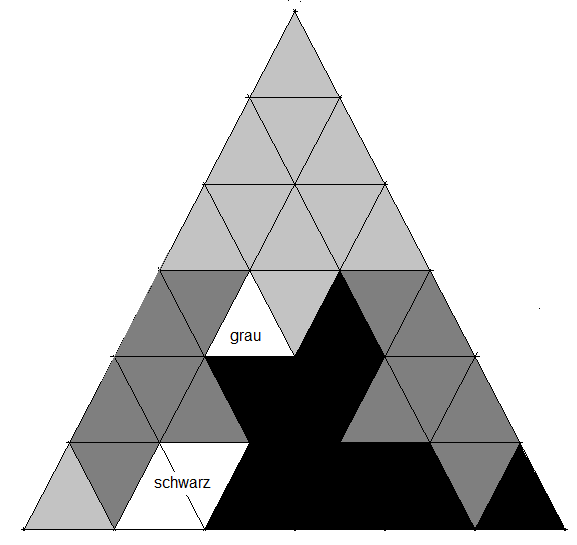
Es genügen acht Teile. Teile gleicher Farbe können jeweils zu einem Stern zusammengesetzt werden.
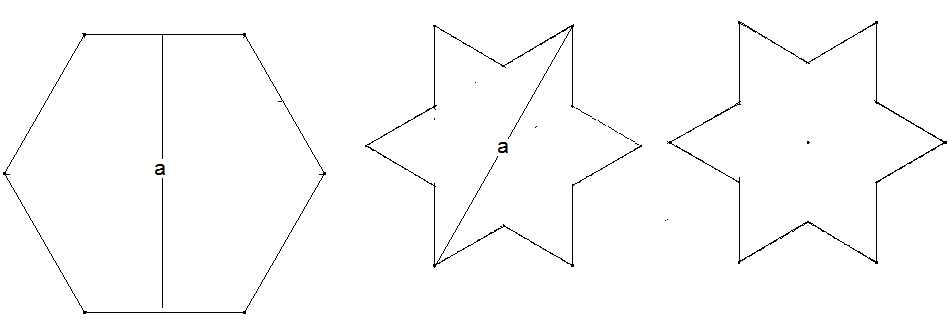
6,2-Sterne und 6,1-Polygon: Zerlegen Sie zwei 6,2-Sterne so in je drei Stücke, dass ein regelmäßiges Sechseck damit ausgelegt werden kann (die mit a bezeichneten Strecken seien gleichlang).
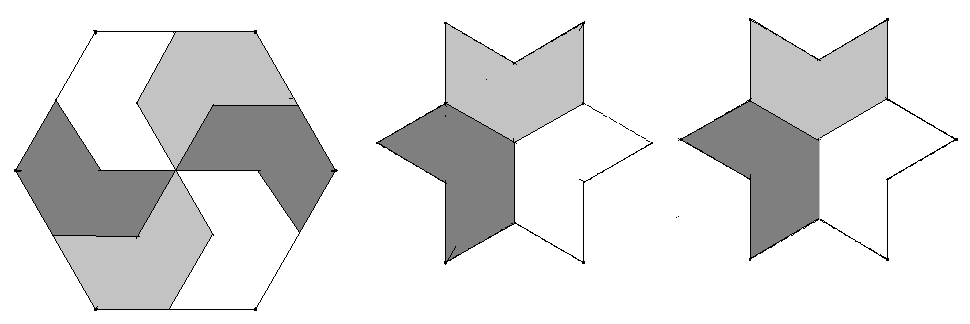
Hier die Zerlegung und die Auslegung:
Papier falten: Es ist leicht, nur durch Falten Seitenhalbierende oder Winkelhalbierende zu konstruieren. Falten Sie ein quadratisches Stück Papier auf zwei verschiedene Arten so, dass die Faltlinien ein regelmäßiges Achteck ergeben.
Erste Möglichkeit:
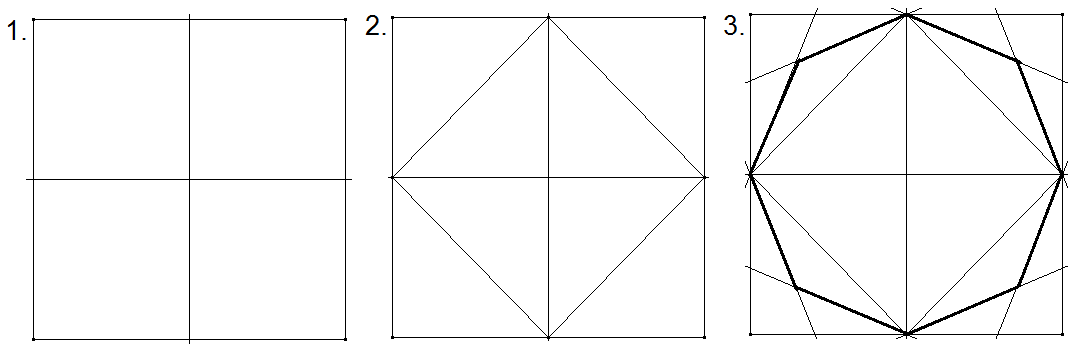
Zweite Möglichkeit:
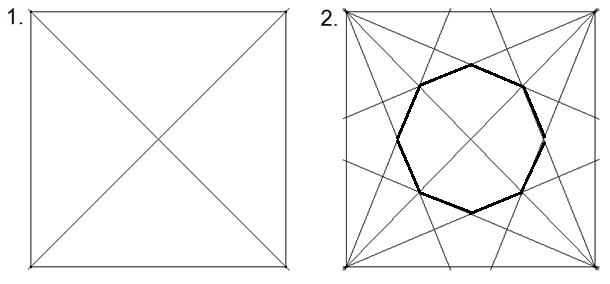
Ein 8,3-Stern: Kann man aus den gegebenen Teilen eines 8,3-Sterns ein regelmäßiges Achteck zusammenlegen?

Ja, so:
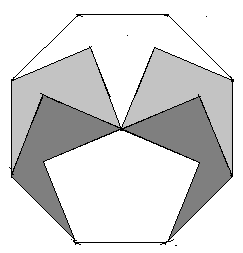
Zackenwinkel: Die Skizze soll darstellen, was unter einem Zackenwinkel bzw. einem Mittelpunkts-winkel eines n,k-Sterns zu verstehen ist. Wenn der Zackenwinkel eines n,k-Sterns doppelt so groß ist wie sein Mittelpunktswinkel dann lässt sich der n,k-Stern zu zwei \(\frac{n}{2}\),j–Sternen umbauen.
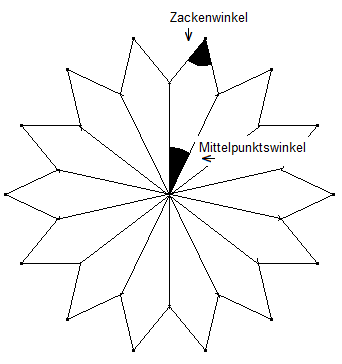
Die Abbildung zeigt einen 14,5-Stern, der sich zu zwei 7,j-Sternen umbauen lässt. Bestimmen Sie j.
Aus einer vorigen Aufgabe wissen wir: Der Zackenwinkel α eines n,k-Sterns berechnet sich als \( α = \frac{180°·(n2k')}{n} \). Für einen 7,j-Stern ergibt sich \( \frac{ 180°·(7 - 2j) }{7} \). Dies soll der Mittelpunktswinkel eines 14,5-Sterns sein, also \( \frac{ 180° · (7 - 2j) }{7} = \frac{ 360° }{14} \). Dann ist 7 - 2j = 1 und j = 3.
Sei n eine gerade Zahl. Welche Beziehung muss zwischen k und j bestehen, damit sich ein n,k-Stern zu zwei \(\frac{n}{2}\),j-Sternen umbauen lässt.
Der Zackenwinkel α eines n,k-Sterns ist \(\frac{ {180^\circ \left( {n - 2k} \right)} }{n}\). Dieser ist doppelt so groß wie sein Mittelpunktswinkel \(\frac{ {360^\circ } }{n}\). Dann ist \( \frac{180°·(n-2k)}{n} = 2·\frac{360°}{n} \) und daher (1) n = 4 + 2k. Der Zackenwinkel eines \(\frac{n}{2}\),j-Sterns ist \( \frac{2·180°·(\frac{n}{2} - 2j)}{n} \). Dies soll der Mittelpunktswinkel eines n,k-Sterns sein, also \( \frac{2·180°·(\frac{n}{2} - 2j)}{n} = \frac{360°}{n} \). Folglich ist (2) \( \frac{n}{2} = 1 + 2j\). (1) in (2) eingesetzt, ergibt \( 1+k=2j \).
