AB: Flächengleichheit/Puzzles (3)
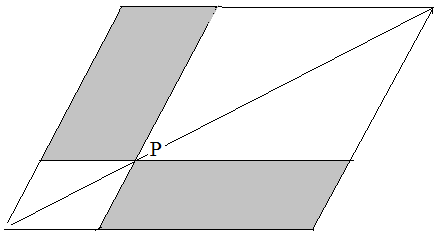
Parallelogramme: Gegeben seien ein Parallelogramm und eine seiner Diagonalen. P sei ein beliebiger Punkt auf der Diagonalen. Durch P wird je eine Parallele zu jeder Parallelogramm-seite gezogen. Zeigen Sie: Die grau unterlegten Parallelogramme sind flächengleich.
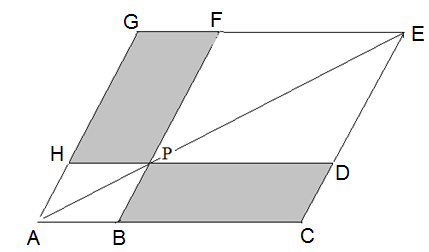
Die Parallelogramme ABPH, PDEF und ACEG werden durch die Diagonale AE in je zwei gleichgroße Flächenstücke zerlegt. Entnimmt man dem Dreieck AEG die weiß unterlegten Flächenstücke und ebenso dem Dreieck ACE, bleiben die grau unterlegten Parallelogramme übrig. HPFG und BCDP sind also flächengleich.
Regelmäßige Sechsecke:
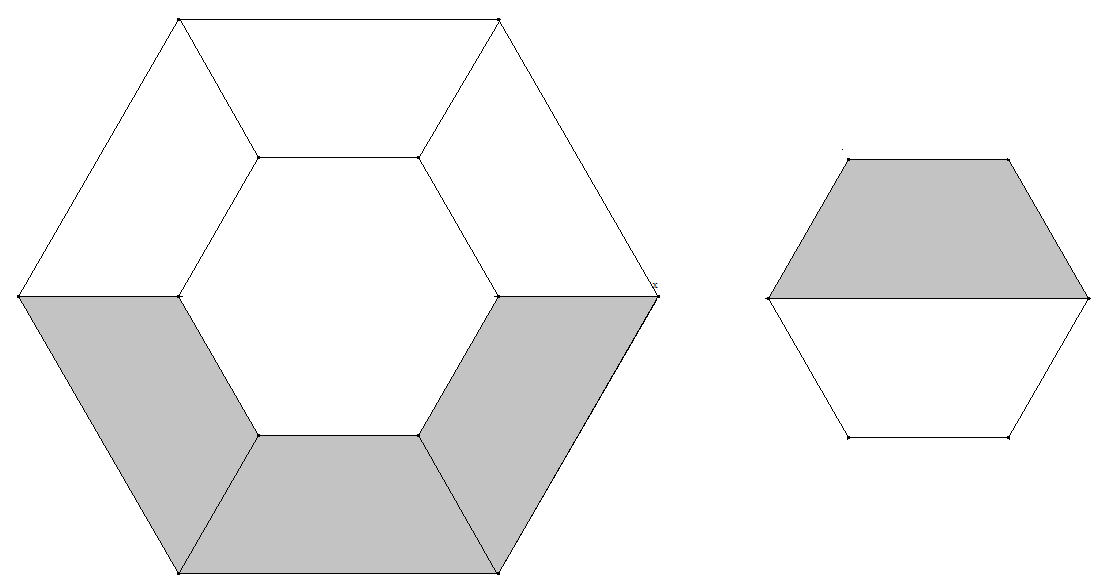
Gegeben sind vier gleichgroße regelmäßige Sechsecke, aus denen Puzzleteile für das Auslegen eines regelmäßigen Sechsecks mit vierfachem Flächeninhalt hergestellt werden sollen. Wie viele Schnitte sind mindestens notwendig?
Drei der vier kleineren Sechsecke werden entlang einer Diagonalen zerschnitten (im Bild rechts). Das vierte bleibt ganz.
Gegeben sind drei gleichgroße regelmäßige Sechsecke aus denen Puzzleteile für das Auslegen eines regelmäßigen Sechsecks mit dreifachem Flächeninhalt hergestellt werden sollen. Eins soll ganz bleiben, eins entlang seiner Diagonalen zerschnitten werden. Wie muss das dritte zerlegt werden?
Hier die Zerlegung des dritten Sechsecks und die Auslegung des großen Sechseck mit den entstandenen Teilen:
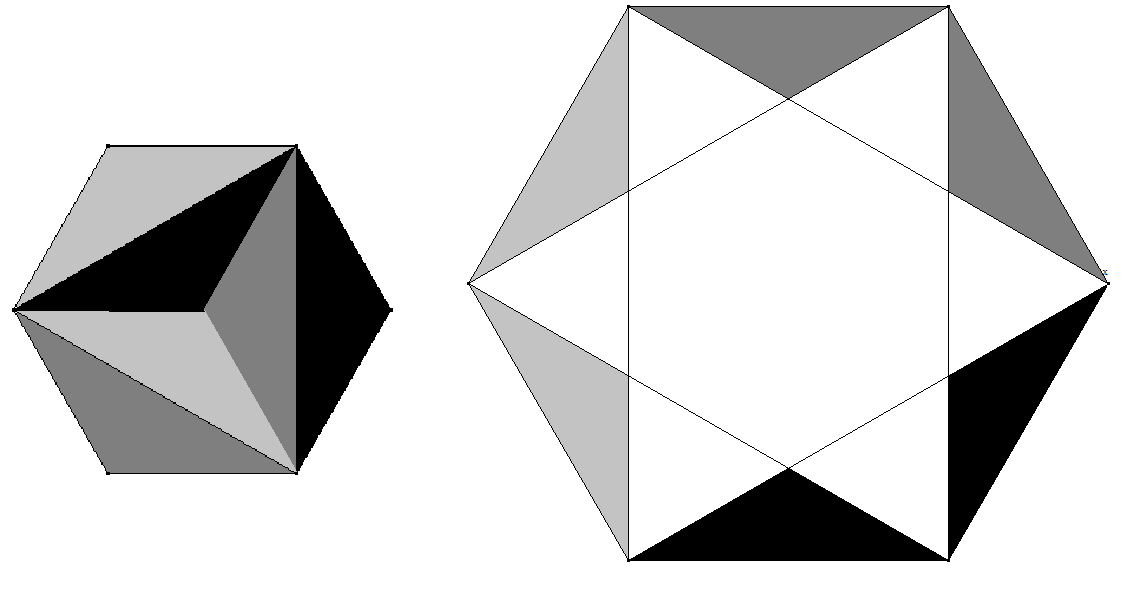
Gegeben sind drei gleichgroße regelmäßige Sechsecke aus denen Puzzleteile für das Auslegen eines regelmäßigen Sechsecks mit dreifachem Flächeninhalt hergestellt werden sollen. Jedes der drei kleineren Sechsecke soll auf die gleiche Weise zerschnitten werden.
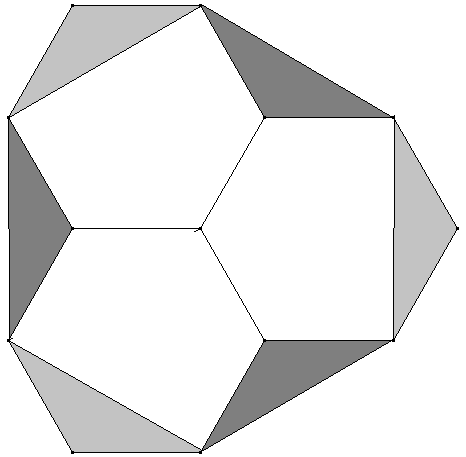
Die hellgrauen Dreiecke werden von den drei kleinen Sechsecken abgeschnitten und als dunkelgraue eingefügt:
Dreiecke zwischen Quadraten:
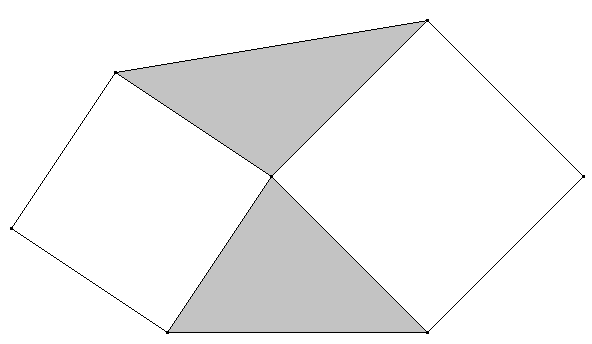
Zwei Quadrate unterschiedlicher Größe haben eine Ecke gemeinsam. Sonst ist die Lage zueinander beliebig. Die gemeinsame Ecke ist gleichzeitig Eckpunkt zweier Dreiecke, welche die Zwischenräume zwischen den Quadraten ausfüllen (in der Abbildung grau unterlegt). Zeigen Sie: Die grauen Dreiecke sind flächengleich.
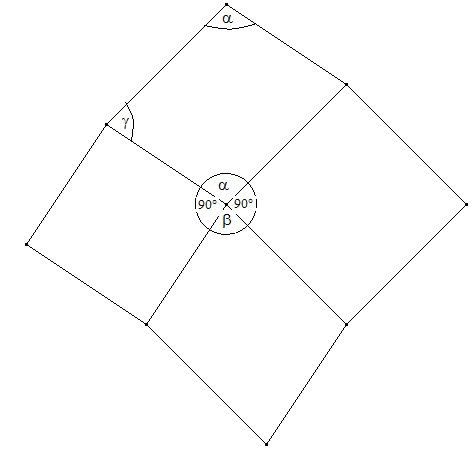
Ergänze die Dreiecke zu Parallelogrammen. Dann ist (1) γ + α = 180° und α + 90° + β + 90° = 360° also (2) α + β = 180°. Wegen (1) und (2) ist β = γ. Parallelogramme sind kongruent, wenn die in zwei unterschiedlichen Seitenlängen und der Größe eines Winkels übereinstimmen. Die grauen Dreiecke der Aufgabe sind Hälften von kongruenten Parallelogrammen und daher flächengleich.
Die Quadrate über den Seiten eines beliebigen Dreiecks werden so ergänzt, dass ihre Zwischenräume von Dreiecken aufgefüllt werden (in der Abbildung grau unterlegt). Zeigen Sie, dass alle grauen Dreiecke flächengleich sind.
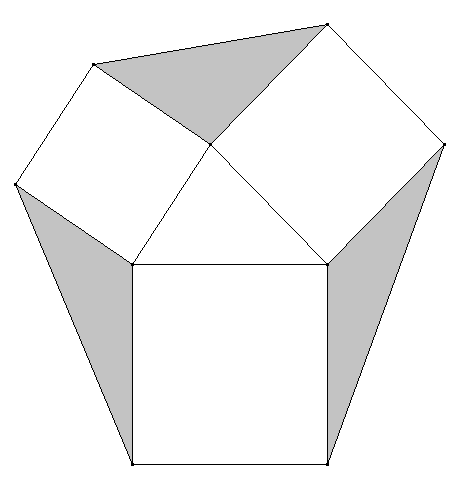
Jedes der grauen Dreiecke ist (nach Aufgabe a) flächengleich zum gleichen Dreieck (in der Mitte). Daher sind alle grauen Dreiecke flächengleich.
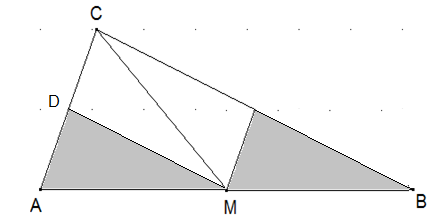
Zerlegung eines Dreiecks: Gegeben sei das Dreieck ABC, und M sei der Mittel-punkt von AB. Zerlegen Sie AMC mit möglichst wenigen geraden Schnitten so, dass MBC aus den Teilstücken von AMC zusammengesetzt werden kann.
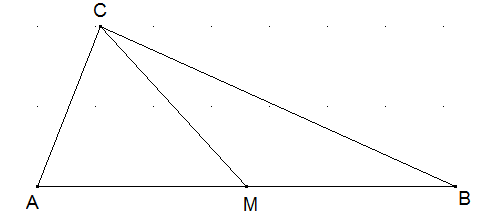
Es genügt ein einziger Schnitt DM parallel zu CB durch M.