AB: Besondere Geometrie-Aufgaben (5)
Ein rechtwinkliges Dreieck: g und h seien zwei sich schneidende Geraden und F ein Punkt auf h. Das Lot in F auf h schneidet g in C. Der Kreis um C mit dem Radius \( | \overline { C F } | \) schneidet g in E und D. Das Lot in E auf g schneidet h in A. Das Lot in D auf g schneidet h in B. Zeigen Sie: ABC ist ein rechtwinkliges Dreieck.
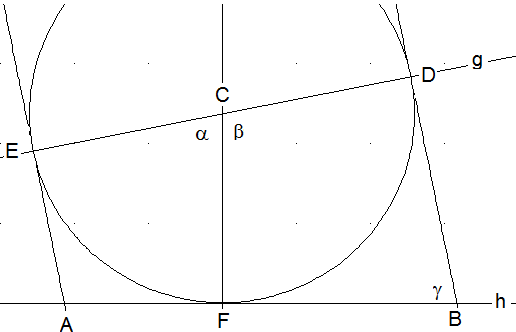
Die Vierecke AFCE und FBDC sind Drachen, denn beide haben zwei aneinander grenzende Paare gleichlanger Seiten (zwei Seiten sind jeweils Radien des gleichen Kreises und je zwei Seiten sind Tangenten an den Kreis von jeweils A bzw. B aus). Die Drachen AFCE und FBDC sind ähnlich, denn sie stimmen in den Winkelgrößen überein (zwei sind rechte und b ergänzt sich sowohl mit a als auch mit g zu 180°). Sowohl AC als auch CB sind Symmetrieachsen der Drachen und halbieren folglich einerseits a und andererseits g. Damit teilt die Höhe CF das Dreieck ABC in zwei ähnliche, rechtwinklige Dreiecke (Übereinstimmung in den Winkelgrößen). Damit ist auch ABC zu diesen Dreiecken ähnlich und rechtwinklig (Dreiecke, die durch eine Höhe in zwei ähnliche zerlegt werden, sind zu beiden Teildreiecken ähnlich).
Flächenverhältnis: In welchem Verhältnis stehen die Flächeninhalte der Rauten zueinander, wenn die Spitzen der Rauten auf dem Kreis die Eckpunkte eines regelmäßigen Sechsecks bilden?
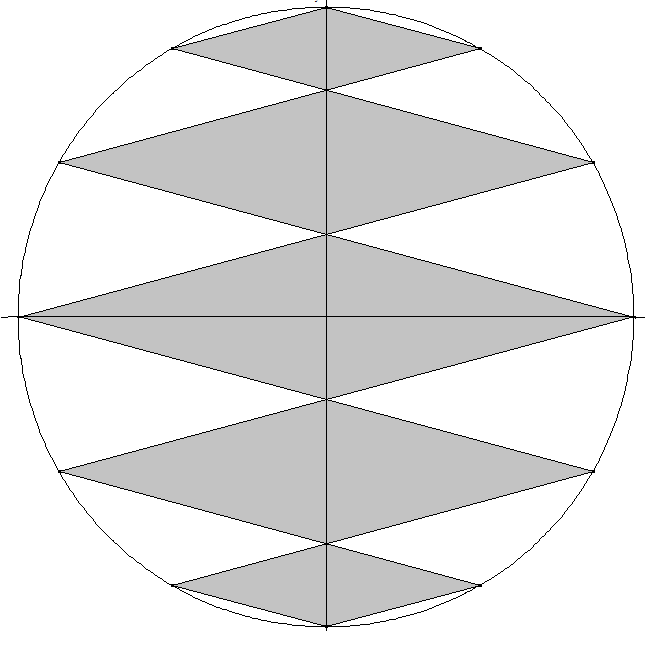
Der Einfachheit halber berechnen wir das Verhältnis der Flächen von Viertelrauten, das ja das gleiche ist, wie das Verhältnis der Flächen der Rauten.
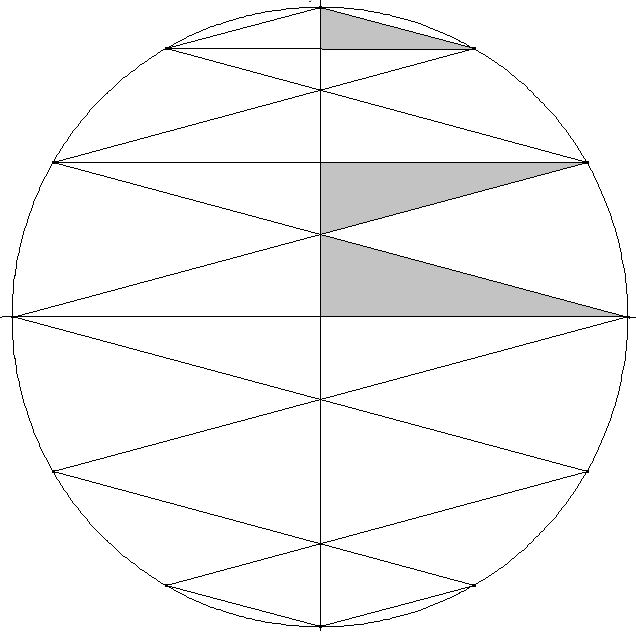
Die Höhe des untersten Dreiecks ist der y-Achsenabschnitt der Gerade durch (0|0) und \( \left( \cos \left( \frac { 5 \pi } { 6 } \right) | \sin \left( \frac { 5 \pi } { 6 } \right) \right) \) und damit 2-√3. Da die Grundseite dieses Dreiecks 1 ist, hat seine Fläche das Maß \( 1 - \frac { \sqrt { 3 } } { 2 } \).
Das Dreieck darüber hat die Höhe \( \sin \left( \frac { \pi } { 6 } \right) - 2 + \sqrt { 3 } = \sqrt { 3 } - \frac { 3 } { 2 } \). Die Grundseite dieses Dreiecks ist \( \cos \left( \frac { \pi } { 6 } \right) = \frac { \sqrt { 3 } } { 2 } \) und der Flächeninhalt ist dann \( \frac { 3 } { 4 } \cdot \left( 1 - \frac { \sqrt { 3 } } { 2 } \right) \).
Das oberste Dreieck hat die Höhe \( 1 - \sin \left( \frac { \pi } { 3 } \right) = 1 - \frac { \sqrt { 3 } } { 2 } \) und die Grundseite \( \cos \left( \frac { \pi } { 3 } \right) = \frac { 1 } { 2 } \) und dann den Flächeninhalt \( \frac { 1 } { 4 } \cdot \left( 1 - \frac { \sqrt { 3 } } { 2 } \right) \). Das Flächenverhältnis der oberen drei Rauten ist demnach \( \frac { 1 } { 4 } : \frac { 3 } { 4 } : 1 \) oder 1:3:4.
Höhenverhältnis: Das Längenverhältnis der der Höhen eines Dreiecks ist umgekehrt proportional zum Längenverhältnis der Seiten, auf denen sie stehen. Zeigen Sie die Gültigkeit des Satzes mit zwei verschieden Beweisen.
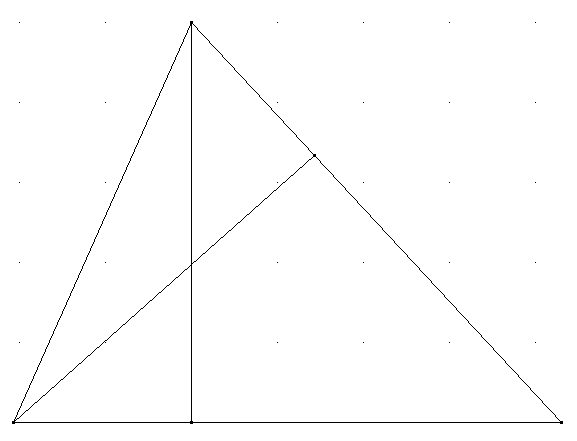
Sei \(\overline { \mathrm { AB } } = \mathrm { c } , \overline { \mathrm { CB } } = \mathrm { a } , \overline { \mathrm { CD } } = \mathrm { h } _ { \mathrm { C } } , \overline { A E } = \mathrm { h } _ { \mathrm { a } } \).
Erster Beweis: Die Dreiecke DBC und ABE sind ähnlich (Übereistimmung in den Winkelgrößen). Dann gilt \( \frac { a } { h _ { c } } = \frac { c } { h _ { a } } \) und daher \( \frac { h _ { a } } { h _ { c } } = \frac { c } { a } \).
Zweiter Beweis: Nach der Flächenformel für Dreiecke gilt: 2A = a·ha = c·hc und daher \( \frac { h _ { a } } { h _ { c } } = \frac { c } { a } \)
Aufgabe von Leon Bankoff: Gegeben seien die Quadrate ABCD und CEFG mit der gemeinsamen Ecke C und den Mittelpunkten M und N. L sei der Mittelpunkt von BE und O sei der Mittelpunkt von DG. Zeigen Sie LMON ist ein Quadrat.
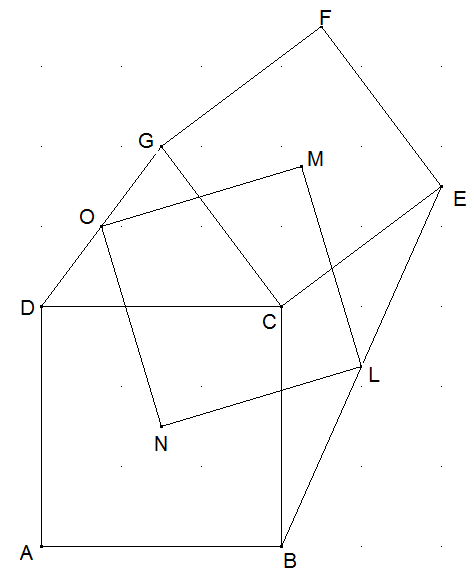
Ergänzen Sie das Dreieck CBE durch Spiegelung an BE und das Dreieck DCG durch Spiegelung an DG jeweils zu einem Parallelogramm. Die Parallelogramme sind kongruent und zwei zugehörige Kongruenz-abbildungen sind Drehungen um 90° um N bzw. um M. Dabei ist L der Bildpunkt von O und die Dreiecke OLM und NLO sind gleichschenklig-rechtwinklig. Damit ist LMON ein Quadrat.
Winkelhalbierende im Viereck: Gegeben sei ein beliebiges Viereck. Je zwei benachbarte Halbierende der Innenwinkel schneiden sich in einem Punkt. Zeigen Sie, dass diese vier Schnittpunkte E, F, G und H ein Sehnenviereck bilden. (Sieht in der Skizze nicht so aus.)
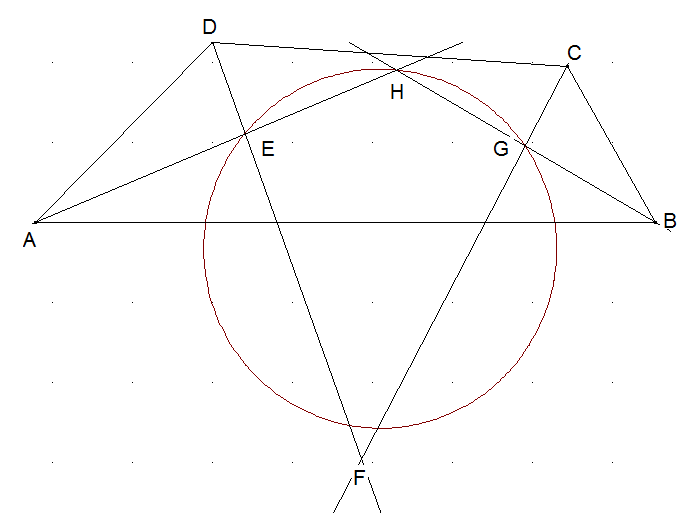
Es gilt:
2α+2β+2γ+2δ=360°
also α+β+γ+δ=180°.
Außerdem ist
ε=δ+γ und μ=α+β
und daher
ε+μ=α+β+γ+δ.
Folglich ergänzen sich gegenüberliegende Ecken des Vierecks EFGH zu 180°. Daher ist das Viereck EFGH ein Sehnenviereck.
