AB: Satz des Pythagoras und verwandte Sätze (7)
Geometrisches Mittel zweier Durchmesser: Gegeben sind zwei sich in C berührende Kreise. A und B seien die Berührpunkte mit einer nicht durch C gehenden gemeinsamen Tangente.
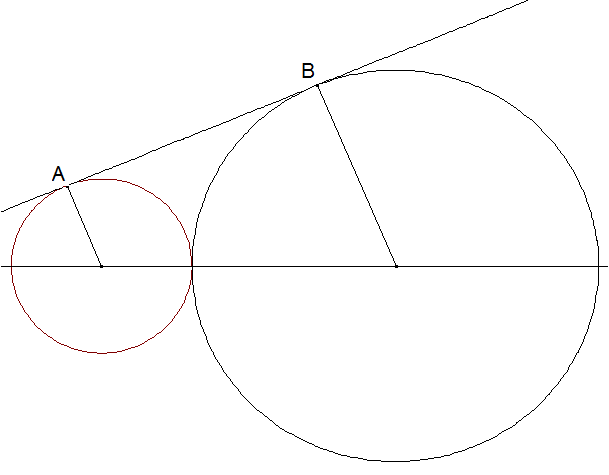
Zeigen Sie: \( | \overline { A B } | ^ { 2 } \) ist das Produkt der beiden Durchmesser.
Die gemeinsame Tangente im Berührpunkt C der beiden Kreise schneidet AB in D. Dann hat D von jedem der drei Punkte A, B und C den gleichen Abstand. (Die Berührpunkte zweier Tangenten an den gleichen Kreishaben von ihrem Schnittpunkt den gleichen Abstand). \( \overline { C D } \) ist gemeinsame Seite zweier Drachenvierecke. (Sind in einem Viereck zwei Paare aneinander grenzender Seiten gleichlang, so ist es ein Drachen). Die Drachenvierecke sind ähnlich zueinander, da sie in den Winkelgrößen übereinstimmen. (Zwei Winkel sind rechte und insbesondere ist a=d, denn beide ergänzen sich mit b zu 180°).
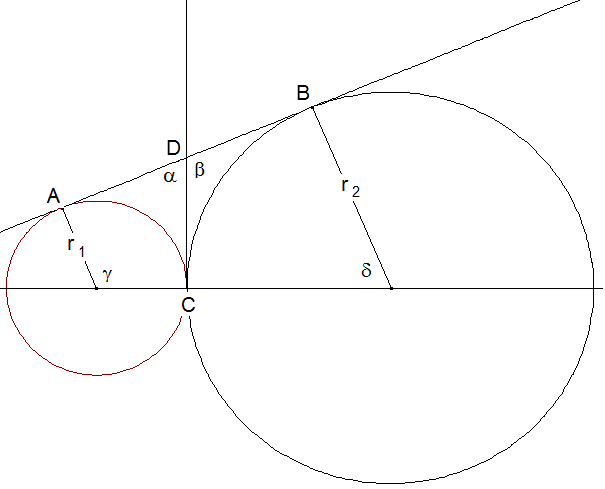
Nennen wir \( \overline { A D } = \overline { D B } = \overline { D C } = a \) dann gilt: \( \frac { r _ { 1 } } { a } = \frac { a } { r _ { 2 } } \) oder r1·r2=a² und dann 2r1·2r2=(2a)².
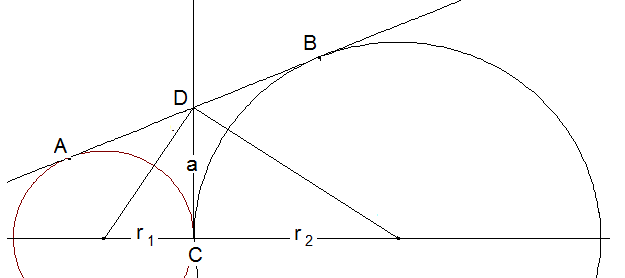
Die gemeinsame Tangente im Berührpunkt C der beiden Kreise schneidet AB in D. Die Mittelpunkte der Kreise seinen M1 und M2. Zeigen Sie: M1M2D ist ein rechtwinkliges Dreieck.
r1 und r2 sind die Abschnitte, in welche der Fußpunkt C der Höhe \( \overline { D C } = a \) der Grundseite M1M2 des Dreiecks M1M2D teilt. Es gilt, wie gezeigt, r1·r2=a². Dies gilt nach der Umkehrung des Höhensatzes nur in rechtwinkligen Dreiecken.
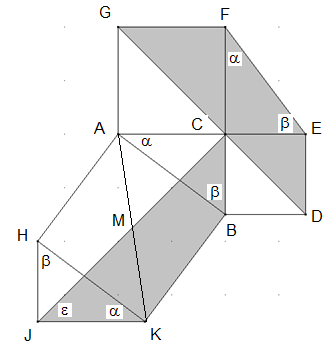
Leonardo da Vinci: Ein rechtwinkliges Dreieck ABC mit den Kathetenquadraten BDEC bzw. ACFG und dem Hypotenusenquadrat HKBA wird um zwei rechtwinklige Dreiecke CEF bzw. HJK ergänzt (siehe Abbildung).
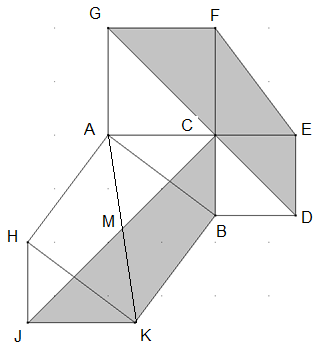
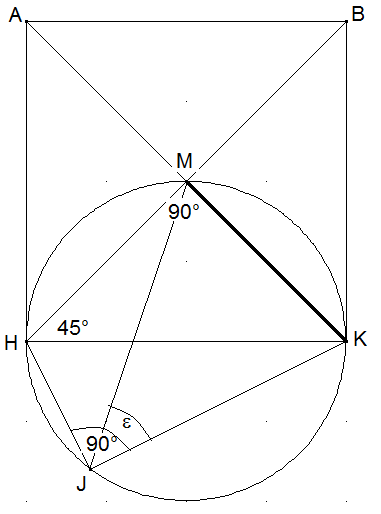
Beweisen Sie den Hilfssatz: „Im rechtwinkligen Dreieck HJK sei J der Scheitelpunkt des rechten Winkels und M der Mittelpunkt des Hypotenusenquadrates. Dann halbiert JM den rechten Winkel.
Im Viereck HJKM haben die Winkel mit den Scheiteln J und M beide die Größe 90°. HJKM ist also ein Sehnenviereck. Der Umfangswinkel über der Sehne MK mit dem Scheitel H hat die Größe 45°. Dann gilt auch e=45°.
Zeigen Sie die Kongruenz der Vierecke JKBC und DEFG.
Das Viereck DEFG hat die Innenwinkel 45°, 90°+b, 90°+α, 45° und drei Seitenlängen der Katheten und der Hypotenuse des rechtwinkligen Dreiecks. Das Viereck JKBC hat die Innenwinkel ε, 90°+β, 90°+α und drei Seitenlängen der Katheten und der Hypotenuse des rechtwinkligen Dreiecks. Nach dem Hilfssatz ist ε = 45° und die Vierecke stimmen in drei Seitenlängen und drei Innenwinkelgrößen überein. Folglich sind sie kongruent.
Leonardo da Vinci hat mit dieser Figur den Satz von Pythagoras bewiesen. Führen Sie den Beweis durch.
Die Spiegelung des Vierecks DEFG an GD erzeugt das Sechseck BDEFGA. Die Drehung des Vierecks JKBC um 180° und um den Punkt M erzeugt das Sechseck JKBCAH. Die Sechsecke sind flächengleich. Sechseck BDEFGA besteht aus zwei rechtwinkligen Dreiecken und den Kathetenquadraten. Sechseck JKBCAH besteht aus zwei rechtwinkligen Dreiecken und dem Hypotenusenquadrat. Dann sind die Kathetenquadrate zusammen so groß, wie das Hypotenusenquadrat.
Quadrate an den Seiten eines Dreiecks: Gegeben ist ein beliebiges Dreieck mit je einem Quadrat an jeder Seite. Die Höhen des Dreiecks werden so weit durchgezogen, dass jede von ihnen ein Quadrat in je zwei Rechtecke zerlegt.
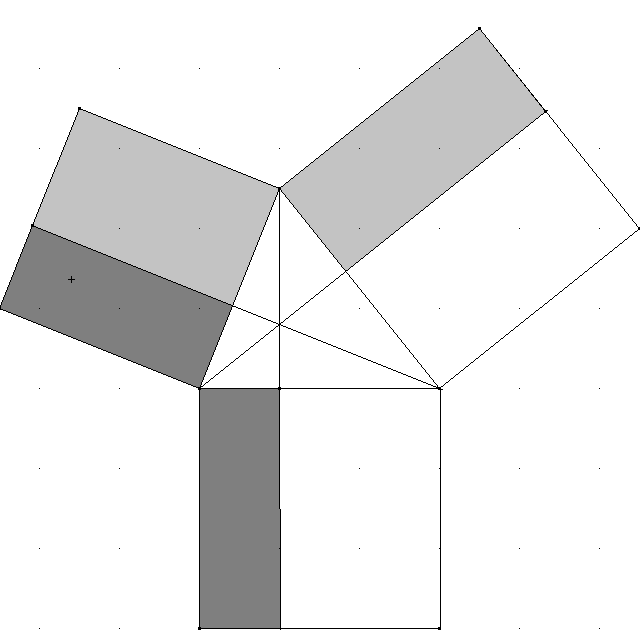
Zeigen Sie, dass aneinander stoßende Rechtecke (gleicher Farbe) flächengleich sind.
In der Skizze sind die schraffierten Quadrate ähnlich zueinander (gleiche Winkel). Daher gilt \( \frac { r } { a } = \frac { s } { b } \). Multiplikation mit a·b führt zu r·b=s·a. Die Rechtecke in der Skizze sind also flächengleich. Der gleiche Beweis gelingt auch für die anderen beiden Rechteckspaare.
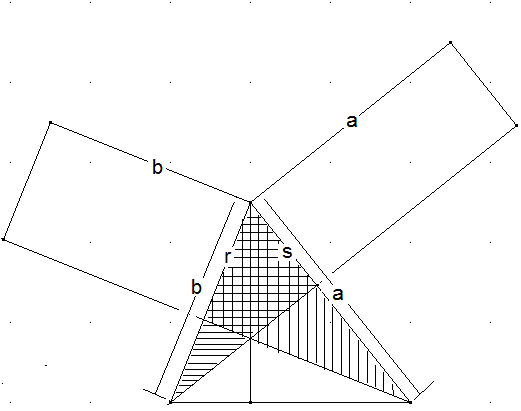
Beweisen Sie auf der Grundlage von a) den Satz des Pythagoras.
Für r=s=0 wird das Dreieck rechtwinklig und die Flächen der Rechtecke mit den Seiten r bzw. s sind ebenfalls gleich 0. Die Rechteckspaare über den Seiten a bzw. b bestehen nur noch aus den Quadraten über a bzw. b. Gleichzeitig zerlegt die dritte Höhe die Seite c in die Abschnitte p und q, sodass p·c=a² und q·c=b². Die Addition dieser beiden Gleichungen führt zu p·c+q·c =a²+b² und wegen p+q=c zu c²= a²+b².
Satz von Raffael: Die gestrichelte Linie ist die Symmetrieachse eines David-sterns. Ein zur Symmetrieachse symmetrisches Rechteck liegt – wie dargestellt – ganz im Inneren des Davidsterns. Eine Seite des Rechtecks oder ihre Verlängerung schneidet eine Seite eines der beiden Dreiecke, aus denen der Sterns besteht in A. Zeigen Sie: Unabhängig von der Breite des Rechtecks sind die beiden fetten Strecken \( \overline { A B } \) und \( \overline { C D } \) gleichlang.
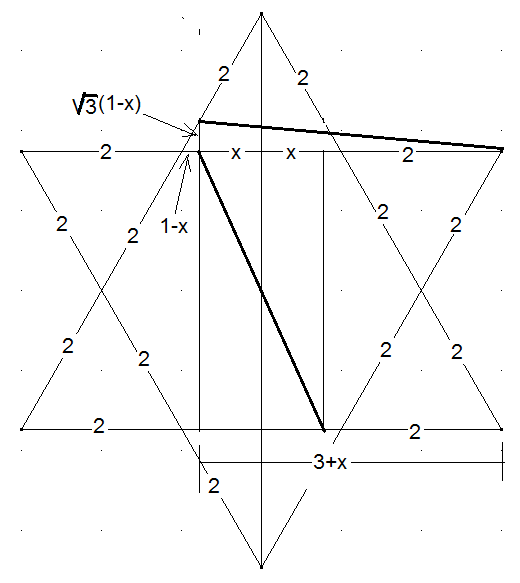
Wir teilen den Davidstern in 12 gleichseitige Dreiecke mit der Seitenlänge 2 und nennen die Rechtecksbreite 2x. Dann lassen sich die Katheten der Dreiecke, deren Hypotenusen die fetten Strecken \( \overline { A B } \) bzw. \( \overline { C D } \)sind, durch Terme von x ausdrücken (siehe Abbildung)
Es bleibt zu zeigen:
3·(1-x)²+(3+x)²= (2x)²+(2√3)². Was leicht zu bestätigen ist. Im Fall x>1 muss lediglich 1 – x durch x – 1 ersetzt werden
Konstruktion von Pappos:
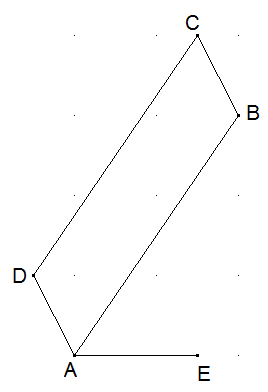
Gegeben sind ein Parallelogramm ABCD und eine Strecke AE wie in der Abbildung. Konstruieren Sie ein Parallelogramm mit der Seite AE flächengleich zu ABCD.
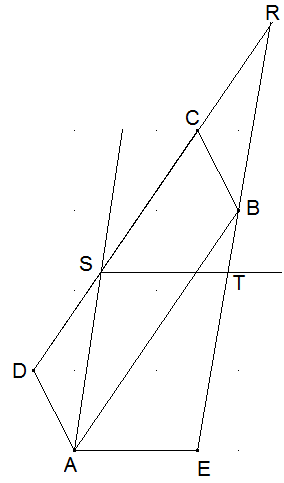
Die Geraden CD und BE schneiden sich in R. Die Parallele zu BE durch A schneidet CD in S. Die Parallelogramme ABCD und ABRS sind flächengleich (gleiche Grundseite AB und gleiche Höhe). Die Parallele zu AE durch S schneidet BE in T. Die Parallelogramme ABRS und AETS sind flächengleich (gleiche Grundseite AS und gleiche Höhe).
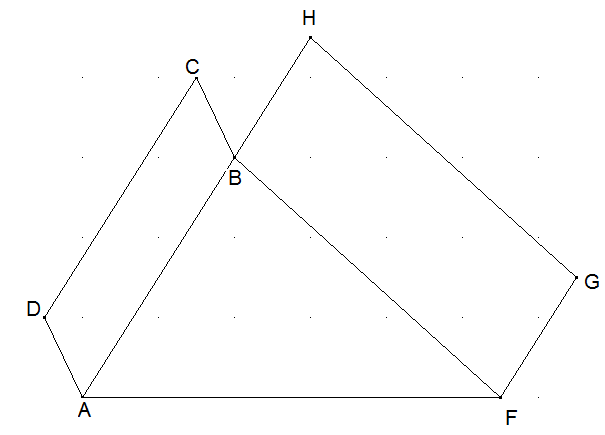
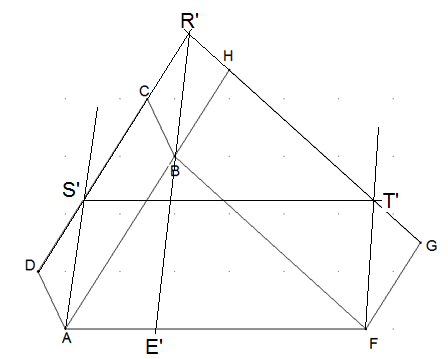
Gegeben ist ein Dreieck AFB, wobei an AB das Parallelogramm ABCD liegt und an FB das Parallelogramm BFGH. Konstruieren Sie ein Parallelogramm mit der Seite AF und einem Flächeninhalt, der so groß ist, wie ABCD und BFGH zusammen.
DC schneidet GH in R‘. R‘B schneidet AF in E‘. Dann ist Aufgabe a) mit E‘ statt E zu lösen. Dann die ent-sprechende Konstruktion für das Parallelo-gramm FGHB und den Punkt E’ durchzuführen. AFT’S‘ ist das gesuchte Parallelogramm.
Begründen Sie, warum unter b) eine starke Verallgemeinerung des Satzes von Pythagoras bewiesen wurde.
Im Falle von Pythagoras sind die Parallelogramme Quadrate und das Dreieck AFB ist rechtwinklig. Außerdem steht RB senkrecht auf der Hypotenuse des rechtwinkligen Dreiecks (und ebenso AS und FT). Dann sind folgende Dreiecke kongruent AFB, DAS, FGT, BHR und BRC. Damit ist das an AF angelegte Parallelogramm das Hypotenusenquadrat.
